【前行】◇第3站◇ 国庆训练营·OI制模拟赛

【第3站】 国庆训练营·OI制模拟赛Ⅰ

怀着冲刺提高组400的愿望来到这个very small but very interesting 的训练营QwQ

在北大dalao的带领下开始了第一场OI模拟赛【炸心态ヽ(*。>Д<)o゜】

---

▶ 简单总结

感觉非常爆炸……

第一题还好，一眼看出结论题，所以开始打表……没想到只打出来了一种情况（为什么全是特殊情况），然后就凉了。

第二题就开始崩溃了。首先画图思考了大概20分钟……然后发现想不出正解，就开始想要骗分。看了看数据阶梯，发现自己好像只能做前1/3的数据，还要码一啪啦代码，顿时整个人都不好了。（脑子一团浆糊）打了一个LCA的版，就为了骗一点分。

第三题……连暴力都不知道怎么写，最后勉强一个搜索结束了整场比赛。

提高组的路还很长，还得慢慢走才行……ˋ( ° ▽、° )

---

（什么鬼“陈太阳”……由于是内部比赛，不能提供提交平台QwQ）

▶ 试题&解析

〔A〕陈太阳与取模

▷题目

给出一个区间[l,r]以及一个整数a，求有多少个整数x，使得对于每一个整数c∈[l,r]满足 c%a≡c (mod x)。如果存在无穷多给=个满足条件的x，输出-1，否则输出x的个数。

[规模] 多组数据（不超过100组），所有数均不超过10¹²。

▷解析

看到题目描述大概就是数学推导了。首先对于取模运算，我们并不陌生，但是我们还可以把它写成带余除法的形式——令 c mod a = b ，c = ka + b (b<a) 。那么我们就可以得到：b ≡ ka + b，也就是说 b mod x = ( ka + b ) mod x。

简单的拆开括号：b mod x = ka mod x + b mod x

移一下项：ka mod x = 0

那么k是什么？ k = [ c / a ] （[]是向下取整）

所以 [ c / a ] * a 是 x 的倍数。

对于 [l,r] 中的每一个 c 都满足上述规律，所以 x 最大为 gcd( [ l / a ] * a , [ ( l + 1 ) / a ] * a , ... , [ r / a ] * a ) = gcd( [ l / a ] , [ ( l + 1 ) / a ] , ... , [ r / a ] ) * a。很容易想到：x的最大值的每一个因数也满足上述规律，那么问题就变成求 x 的最大值的因子个数。

首先因为 { [ l / a ] , [ ( l + 1 ) / a ] , ... , [ r / a ] } 是一个连续的非降序列，而相邻的两个正整数都是互质的，所以如果 [ l / a ] ≠ [ r / a ] ，则它们的gcd就等于1，否则它们就全都相等（也就是 [ l / a] ），则gcd为 [ l / a ] 。这样我们就可以求得x的最大值，从而以根号x的复杂度分解因数，就可以得到答案。

总体时间复杂度为 O( t * sqrt(a) )。

▷源代码

/*Lucky_Glass*/
//陈太阳与取模
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
int main(){
    int T;scanf("%d",&T);
    while(T--){
        ll l,r,a;
        scanf("%lld%lld%lld",&l,&r,&a);
        if(r<a){
            printf("-1");
            continue;
        }
        ll num,tot=0;
        if(l/a==r/a) num=l/a;
        else num=a;
        for(ll i=1;i*i<=num;i++){
            if(num%i==0){
                ll A=i,B=num/i;
                if(A==B) tot++;
                else tot+=2;
            }
        }
        printf("%lld",tot);
    }
    return 0;
}

〔B〕陈太阳与路径

▷题目

给出一个n个节点的树，对于每一个节点，求出它是多少条路径的中点（路径没有方向性，即 u->v 等同于 v->u ）。

[规模] n≤500000

[注意] 路径的起点和终点可以是同一个点

▷解析

由于要统计个数，而且n比较大，还容易想到树形DP。

我们先固定1作为树根，那么对于一个节点u，如果以u为终点，那么路径的两端点有3种情况：

①在 u 的两个不同的子节点的子树中；

②一个在u的一个子节点的子树中，另一个是u的一个祖先；

③一个在u的一个子节点的子树中，另一个在u的一个祖先的子节点v（u不在v的子树中）的子树中。

举个例子：

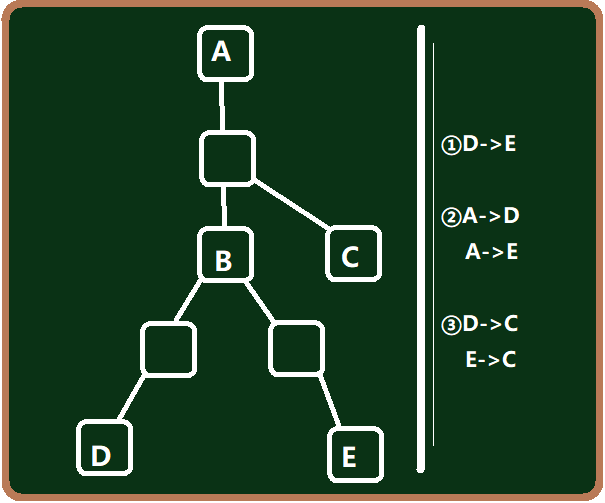
那么我们可以记从点u向下走i步能够走到的点的个数为 g[u][i] ，记从点u先向上走一步，再走（随意走，只要不回到u）(i-1) 步能走到的点的个数为 f[u][i]。

先求g[u][i]：

设v是u的一个儿子，那么g[u][i]则等于所有g[v][i-1]的和（先走到儿子v，再从v向下走i-1步）。

那么从根节点出发，一遍DFS就可以了。

再求f[u][i]，需要用到 g：

设fa是u的父亲，那么f[u][i]可以理解为先走到父亲，再从父亲向上走一层到祖先，然后从祖先走(i-2)步，也就是f[fa][i-1]；或者从父亲向下走(i-1)步，也就是g[fa][i-1]，但是我们不能回到u，就必须减去从fa又走到u的情况，这时候可以看成从 u 出发向下走(i-2)步，也就是g[u][i-2]。所以最后可以得到：

f[u][i] = f[fa][i-1] + g[fa][i-1] - g[u][i-2]；

当然我们会碰到i-2<0的情况，这时候就只减去回到u的情况，也就是减去1：

f[u][i] = f[fa][i-1] + g[fa][i-1] - 1；

这也可以一遍DFS做完。

最后统计答案其实可以在两遍DFS中一并求出，具体就看代码了……

▷源代码

/*Lucky_Glass*/
//陈太阳与路径
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;

typedef long long ll;
const int N=500000;

int n;
vector<int> lnk[N+5];
int max_dep[N+5],fa[N+5];
vector<int> g[N+5],f[N+5];//down up
ll ans[N+5];

void DFS1(int u,int pre){
	fa[u]=pre;
	for(int i=0;i<lnk[u].size();i++){
		int v=lnk[u][i];
		if(v==pre) continue;
		DFS1(v,u);
		max_dep[u]=max(max_dep[u],max_dep[v]);
	}
	max_dep[u]++;
	g[u].resize(max_dep[u]);f[u].resize(max_dep[u]);
	g[u][0]=1;
	for(int i=0;i<lnk[u].size();i++){
		int v=lnk[u][i];
		if(v==pre) continue;
		for(int j=1;j<=max_dep[v];j++){
			ans[u]+=1ll*g[v][j-1]*g[u][j];
			g[u][j]+=g[v][j-1];
		}
	}
}
void DFS2(int u){
	f[u][0]=1;
	if(u==1) ans[u]++;//1'self
	else{
		for(int i=1;i<max_dep[u];i++){
			f[u][i]=f[fa[u]][i-1]+g[fa[u]][i-1];
			if(i>=2) f[u][i]-=g[u][i-2];
			else f[u][i]--;
		}
		for(int i=0;i<max_dep[u];i++)
			ans[u]+=f[u][i]*g[u][i];
	}
	for(int i=0;i<lnk[u].size();i++)
		if(lnk[u][i]!=fa[u])
			DFS2(lnk[u][i]);
}
int main(){
	scanf("%d",&n);
	for(int i=1,u,v;i<n;i++){
		scanf("%d%d",&u,&v);
		lnk[u].push_back(v);
		lnk[v].push_back(u);
	}
	DFS1(1,0);
	DFS2(1);
	printf("%lld",ans[1]);
	for(int i=2;i<=n;i++)
		printf(" %lld",ans[i]);
	return 0;
}

　　

---

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我，在周末我会尽量解答并完善博客~