洛谷——P1033 自由落体

P1033 自由落体

题目描述

在高为 H 的天花板上有 n 个小球，体积不计，位置分别为 0，1，2，…．n-1。在地面上有一个小车（长为 L，高为 K，距原点距离为 S1）。已知小球下落距离计算公式为 d＝1/2*g*(t^2)，其中 g=10，t 为下落时间。地面上的小车以速度 V 前进。

如下图：

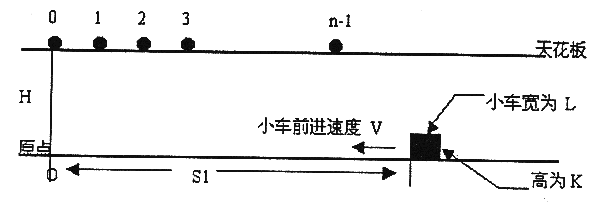
小车与所有小球同时开始运动，当小球距小车的距离 <= 0.0001(感谢Silver_N修正) 时，即认为小球被小车接受（小球落到地面后不能被接受）。

请你计算出小车能接受到多少个小球。

输入输出格式

输入格式：

键盘输人：

H，S1，V，L，K，n （l<=H，S1，V，L，K，n <=100000）

输出格式：

屏幕输出：

小车能接受到的小球个数。

输入输出样例

输入样例#1： 复制

5.0 9.0 5.0 2.5 1.8 5

输出样例#1： 复制

1

说明

当求落入车的尾部时，算作落入车内。

数学计算+模拟

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int L1,L2,n,ans;
double H,h,v,l,t,s,s1,s2;
int main()
{
    scanf("%lf%lf%lf%lf%lf%d",&H,&s1,&v,&l,&h,&n);
    t=sqrt(*(H-h)/);
    s=s1-t*v;
    L2=s+l;
    t=sqrt(*H/);
    L1=max(,int(s1-t*v));
    ans=min(L2-L1,n-L1);
    printf("%d",ans);
    ;
}