转：增强学习（二）----- 马尔可夫决策过程MDP

1. 马尔可夫模型的几类子模型

大家应该还记得马尔科夫链(Markov Chain)，了解机器学习的也都知道隐马尔可夫模型(Hidden Markov Model，HMM)。它们具有的一个共同性质就是马尔可夫性(无后效性)，也就是指系统的下个状态只与当前状态信息有关，而与更早之前的状态无关。

马尔可夫决策过程(Markov Decision Process, MDP)也具有马尔可夫性，与上面不同的是MDP考虑了动作，即系统下个状态不仅和当前的状态有关，也和当前采取的动作有关。还是举下 棋的例子，当我们在某个局面（状态s）走了一步(动作a)，这时对手的选择（导致下个状态s’）我们是不能确定的，但是他的选择只和s和a有关，而不用考 虑更早之前的状态和动作，即s’是根据s和a随机生成的。

我们用一个二维表格表示一下，各种马尔可夫子模型的关系就很清楚了：

	不考虑动作	考虑动作
状态完全可见	马尔科夫链(MC)	马尔可夫决策过程(MDP)
状态不完全可见	隐马尔可夫模型(HMM)	不完全可观察马尔可夫决策过程(POMDP)

2. 马尔可夫决策过程

一个马尔可夫决策过程由一个四元组构成M = (S, A, P_sa, R)

MDP 的动态过程如下：某个智能体(agent)的初始状态为s₀，然后从 A 中挑选一个动作a₀执行，执行后，agent 按P_sa概率随机转移到了下一个s₁状态，s₁∈ P_s0a0。然后再执行一个动作a₁，就转移到了s₂，接下来再执行a₂…，我们可以用下面的图表示状态转移的过程。

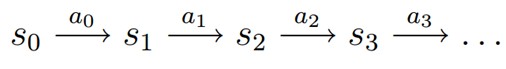
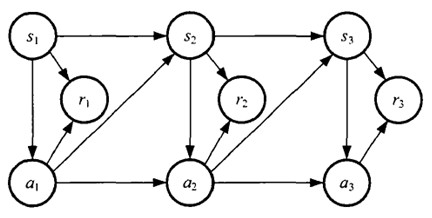
如果回报r是根据状态s和动作a得到的，则MDP还可以表示成下图：

3. 值函数(value function)

上篇我们提到增强学习学到的是一个从环境状态到动作的映射（即行为策略），记为策略π: S→A。而增强学习往往又具有延迟回报的特点: 如果在第n步输掉了棋，那么只有状态s_n和动作a_n获得了立即回报r(s_n,a_n)=-1，前面的所有状态立即回报均为0。所以对于之前的任意状态s和动作a，立即回报函数r(s,a)无法说明策略的好坏。因而需要定义值函数(value function，又叫效用函数)来表明当前状态下策略π的长期影响。

用V^π(s)表示策略π下，状态s的值函数。r_i表示未来第i步的立即回报，常见的值函数有以下三种：

a)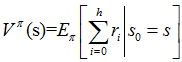

b)

c)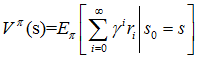

其中：

a)是采用策略π的情况下未来有限h步的期望立即回报总和；

b)是采用策略π的情况下期望的平均回报；

c)是值函数最常见的形式，式中γ∈[0,1]称为折合因子，表明了未来的回报相对于当前回报的重要程度。特别的，γ=0时，相当于只考虑立即不考虑长期回报，γ=1时，将长期回报和立即回报看得同等重要。接下来我们只讨论第三种形式，

现在将值函数的第三种形式展开，其中r_i表示未来第i步回报，s'表示下一步状态，则有：

给定策略π和初始状态s，则动作a=π(s)，下个时刻将以概率p(s'|s,a)转向下个状态s'，那么上式的期望可以拆开，可以重写为：

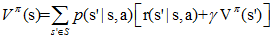
上面提到的值函数称为状态值函数(state value function)，需要注意的是，在V^π(s)中，π和初始状态s是我们给定的，而初始动作a是由策略π和状态s决定的，即a=π(s)。

定义动作值函数(action value functionQ函数)如下：

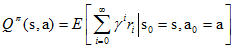
给定当前状态s和当前动作a，在未来遵循策略π，那么系统将以概率p(s'|s,a)转向下个状态s'，上式可以重写为：

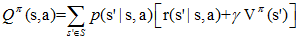
在Q^π(s,a)中，不仅策略π和初始状态s是我们给定的，当前的动作a也是我们给定的，这是Q^π(s,a)和V^π(a)的主要区别。

知道值函数的概念后，一个MDP的最优策略可以由下式表示：

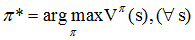
即我们寻找的是在任意初始条件s下，能够最大化值函数的策略π*。

4. 值函数与Q函数计算的例子

上面的概念可能描述得不够清晰，接下来我们实际计算一 下，如图所示是一个格子世界，我们假设agent从左下角的start点出发，右上角为目标位置，称为吸收状态(Absorbing state)，对于进入吸收态的动作，我们给予立即回报100，对其他动作则给予0回报，折合因子γ的值我们选择0.9。

为了方便描述，记第i行，第j列的状态为s_ij, 在每个状态，有四种上下左右四种可选的动作，分别记为a_u,a_d,a_l,a_r。（up，down，left，right首字母），并认为状态按动作a选择的方向转移的概率为1。

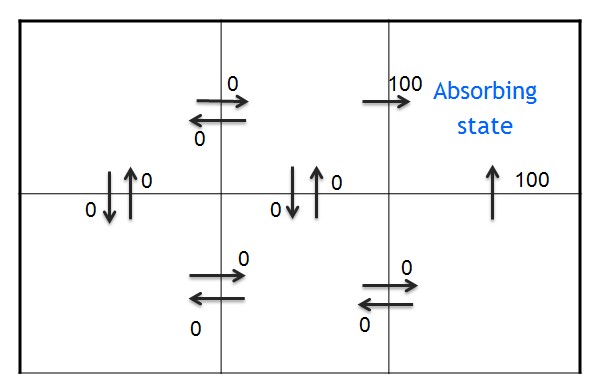
1.由于状态转移概率是1，每组(s,a)对应了唯一的s'。回报函数r(s'|s,a)可以简记为r(s,a)

如下所示，每个格子代表一个状态s，箭头则代表动作a，旁边的数字代表立即回报，可以看到只有进入目标位置的动作获得了回报100，其他动作都获得了0回报。　即r(s₁₂,a_r) = r(s₂₃,a_u) =100。

2. 一个策略π如图所示：

3. 值函数V^π(s)如下所示

根据V^π的表达式，立即回报，和策略π，有

V^π(s₁₂) = r(s₁₂,a_r) = r(s₁₃|s₁₂,a_r) = 100

V^π(s₁₁)= r(s₁₁,a_r)+γ*V^π(s₁₂) = 0+0.9*100 = 90

V^π(s₂₃) = r(s₂₃,a_u) = 100

V^π(s₂₂)= r(s₂₂,a_r)+γ*V^π(s₂₃) = 90

V^π(s₂₁)= r(s₂₁,a_r)+γ*V^π(s₂₂) = 81

4. Q(s,a)值如下所示

有了策略π和立即回报函数r(s,a), Q^π(s,a)如何得到的呢？

对s₁₁计算Q函数（用到了上面V^π的结果）如下：

Q^π(s₁₁,a_r)=r(s₁₁,a_r)+ γ *V^π(s₁₂)  =0+0.9*100 = 90

Q^π(s₁₁,a_d)=r(s₁₁,a_d)+ γ *V^π(s₂₁)  = 72

至此我们了解了马尔可夫决策过程的基本概念，知道了增强学习的目标（获得任意初始条件下，使V^π值最大的策略π*），下一篇开始介绍求解最优策略的方法。

PS:发现写东西还是蛮辛苦的，希望对大家有帮助。另外自己也比较菜，没写对的地方欢迎指出~~

[注]采用折合因子作为值函数的MDP也可以定义为五元组M=(S, A, P, γ, R)。也有的书上把值函数作为一个因子定义五元组。还有定义为三元组的，不过MDP的基本组成元素是不变的。

参考资料：

[1] R.Sutton et al. Reinforcement learning: An introduction , 1998

[2] T.Mitchell. 《机器学习》，2003

[3] 金卓军，逆向增强学习和示教学习算法研究及其在智能机器人中的应用[D]，2011

[4] Oliver Sigaud et al，Markov Decision Process in Artificial Intelligence[M], 2010