邓俊辉数据结构学习-7-BST

二叉搜索树(Binary-Search-Tree)--BST

要求：AVL树是BBST的一个种类，继承自BST，对于AVL树，不做太多掌握要求

1. 四种旋转，旋转是BBST自平衡的基本，变换，主要掌握旋转的思想。
2. 3+4重构，重点明白为什么可以3+4重构，而不是使用旋转
3. 对于AVL插入和删除做了解，知道其为什么比不过红黑树就可以了。

循关键码访问(call-by-key)

• 关键码：就是所谓的key
• 条件：
  • 关键码之间支持大小比较
  • 支持相等比对
• 在BST中，所有数据都统一实现和表示为entry(entry是什么?)

entry(词条)其实就是(key-value)对

同时还支持大小比较和相等比对(通过比较词条的key)的方式。

概念

• 词条，二叉树的节点，关键码三者之间在不做具体强调的时候，概念等同。

BST特征

1. 顺序性：任意节点均不小于其左后代。且其右后代也均不小于其节点。
   • 数学语言描述就是 one-of-left-node <= V <= one-of-right-node
   • 注意这里是后代，不是孩子
2. 简化条件：禁止重复词条, 意识就是目前不考虑重复key的存在
   • 经过简单扩容后就可以支持重复词条。
3. BST的中序遍历必然单调。因此就得到了判断树是否是BST的方法。

注意key-value的映射为单一映射，不存在单一key映射多个value，但不同key可以映射相同value，具体

设计看自己

接口

查找 search

search查找的本质就是二分查找。

BST<T>::searchIn(BinNodePos(T) &v  , const T &key, BinNodePos(T) &hot /*记忆热点*/)
{
    if(!v || (key == v->data))    return v;
    hot = v;
    return searchIn(( key < v->data ? v->lc : v->rc), key, hot);

• 代码本身没有难度，这里主要注重接口语义：
  • hot的语义： 查找成功时，返回命中节点的父亲。 查找失败时，返回最后返回的一个存在的非空节点。
  • 语义统一： 假设我们在查找失败的时候引入假想的哨兵节点，且其key值正好等于我们要找的key。则search
    
    返回的就是目标节点。hot返回的就是目标节点的父亲。
  • 注意返回值，和第一个参数，都是使用的指针的引用。这样做的目的是让search的返回值后续被其他接口
    
    调用，而且主需要改变这个返回值，就可以改变指针的指向，所以指针配合引用的方式取缔了二级指针的使用，
    
    熟悉了后，感到很方便。

插入 insert

再次重申，我们当前认为不存在重复节点。那么，我们要插入的元素，通过search(e)接口的调用，

就会发现返回的位置恰好就是我们当初假想的哨兵。也就是e应该存在的位置。

那么就很简单了, 直接操作返回位置。就可以了。

现在明白为什么当初返回的是BinNodePos(T) & 了。

BinNodePos(T)
BST<T>::insert(const T &e)
{
    BinNodePos(T) x = search(e);
    if(!x) // 保证插入元素不存在
    {
        x = new BinNode(e, _hot); // 很方便的完成了parent的回指，
        /* ----- 要记得维护该有的数据项 ----- */
        ++_size;
        updateHeightAbove(_hot); // 从插入节点的父亲节点开始更新高度，逐步向上
    }
    return x;
}

有些数据结构时不维护height的，但是接下使用的AVL树需要使用height

删除 remove

删除同插入一样，在删除之后，依然要保持这个BST的有序性。而且同样需要维护height和size。

因此，删除比较复杂的情况在于删除目标元素后，目标元素后面的元素有一个替换的过程。

bool remove(const T &e)
{
    BinNodePos(T) x = search(e);
    if(!x) return false;
    removeAt(x, _hot);
    --_size;
    updateHeightAbove(_hot);
    return true;
}

void removeAt(BinNodePos(T) &x, BinNodePos(T) &hot)
{
    BinNodePos(T) w = x; // 保存删除节点位置
    BinNodePos(T) succ = nullptr;
    if(!x->lc && !x->rc)
    {
        // do nothing
    }
    else if(!x->lc) // 左树为空的情况下
    {
        succ = x = x->rc;
        /* 拆开来理解
        x = x->rc;  直接让删除节点的后继覆盖删除节点
        succ = x; 然后然明文后继指向后继，标记后继位置
        */
    }
    else if(!x->rc)
    {
        succ = x = x->lc;
    }
    else{ // 哇，最喜欢这里
        w = w->succ(); // w指向自己的中序后继, 这里要从中序遍历的序列理解，删除一个树的节点，
       // 我们先将这个树的值和其中序遍历后继替换再删，就是相当于交换了有序的向量 的下一个值，然后删下
       // 个值，没有任何影响，但是这个节点的中序遍历后继最多只可能有一个孩子, 因为当前节点左右孩子
       // 都有，那么其后继一定在右孩子中的最左分支。那么其就不能有右孩子。最多只能有一个右孩子。
        std::swap(w->data, x->data);
        // 到目前为止，w依然保留着删除节点位置（虽然它动了）
        BinNodePos(T) u = w->parent;
        if(u == x) // 即使w->rc为nullptr也没关系
            u->rc = succ = w->rc;
        else
            u->lc = succ = w->rc
    }
    hot = w->parent;
    if(succ) succ->parent = hot; // 如果删除节点的后继存在，还要进行回指
    release(w->data);
    release(w);
    return succ;
}
/* 只会出现俩种情况 情况1
                                                                                     .─.
                 .─.                                                                ( X )
                ( X )   <- u                                                       ▪ `─' ▪
                ▪`─'▪                                                            ▪        ▪
               ▪     ▪                                                         ▪           ▪ .─.
              ▪       ▪.─.                                                   ▪              (   )
          ▪ ▪         ( W )                                                 ▪               ▪`─'
         ▪▪▪           `─'▪                                             ▪ ▪             .─.▪
        ▪   ▪              ▪                                           ▪▪▪        u->  (...) ◀┐
       ▪     ▪              ▪                                         ▪   ▪            ▪`─'   │  ┌────────────────┐
      ▪       ▪              ▪                                       ▪     ▪          ▪       └──│ may many nodes │
     ▪         ▪            ▪▪▪          ┌──────────────┐           ▪       ▪     .─.▪           └────────────────┘
    ▪     T     ▪          ▪   ▪      ┌──│may not exist │          ▪         ▪   ( W )
   ▪             ▪        ▪     ▪     │  └──────────────┘         ▪     T     ▪   `─'▪
  ▪               ▪      ▪       ▪    │                          ▪             ▪      ▪
 ▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪    ▪         ▪ ◀─┘                         ▪               ▪      ▪
                       ▪     T     ▪                           ▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪      ▪
                      ▪             ▪                                                  ▪▪▪          ┌──────────────┐
                     ▪               ▪                                                ▪   ▪      ┌──│may not exist │
                    ▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪                                              ▪     ▪     │  └──────────────┘
                                                                                    ▪       ▪    │
                                                                                   ▪         ▪ ◀─┘
                                                                                  ▪     T     ▪
                                                                                 ▪             ▪
                                                                                ▪               ▪
                                                                               ▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪▪
*/

平衡与代价

BST的所有查找，插入，删除均为O(h)的复杂度。

注意BST的高度并不是log(N);

最坏情况下是线性排列，那么h = n

这也就引入了AVL树和RB树。

理想平衡

在理想平衡下，树的高度总共不会超过logN，但是需要注意的是，维护这样一种状态，在插入和删除后进行的

状态调整代价可能会很高，因为我们寻求的是一种适度平衡。

平衡二叉搜索树 Balance-BST -- BBST

注意：对于BBST来说，仍然要保持BST的有序性，即中序遍历的序列不能发生变化。

这样俩个BST，我们称为等价BST，利用的就是中序遍历的歧义性。

等价BST变换规律：

1. 上下可变: 祖先和后代关系可以发生颠倒, 在垂直方向有一定自由度
2. 左右不乱: 在节点左侧的节点，经过调整后，依然在左侧，在右侧的节点经过调整后依然在右侧。

基本变换

任何BST之间的等价变换都是经过一系列的基本变换形成的。详细证明可以参考《数据结构与算法分析》

旋转操作

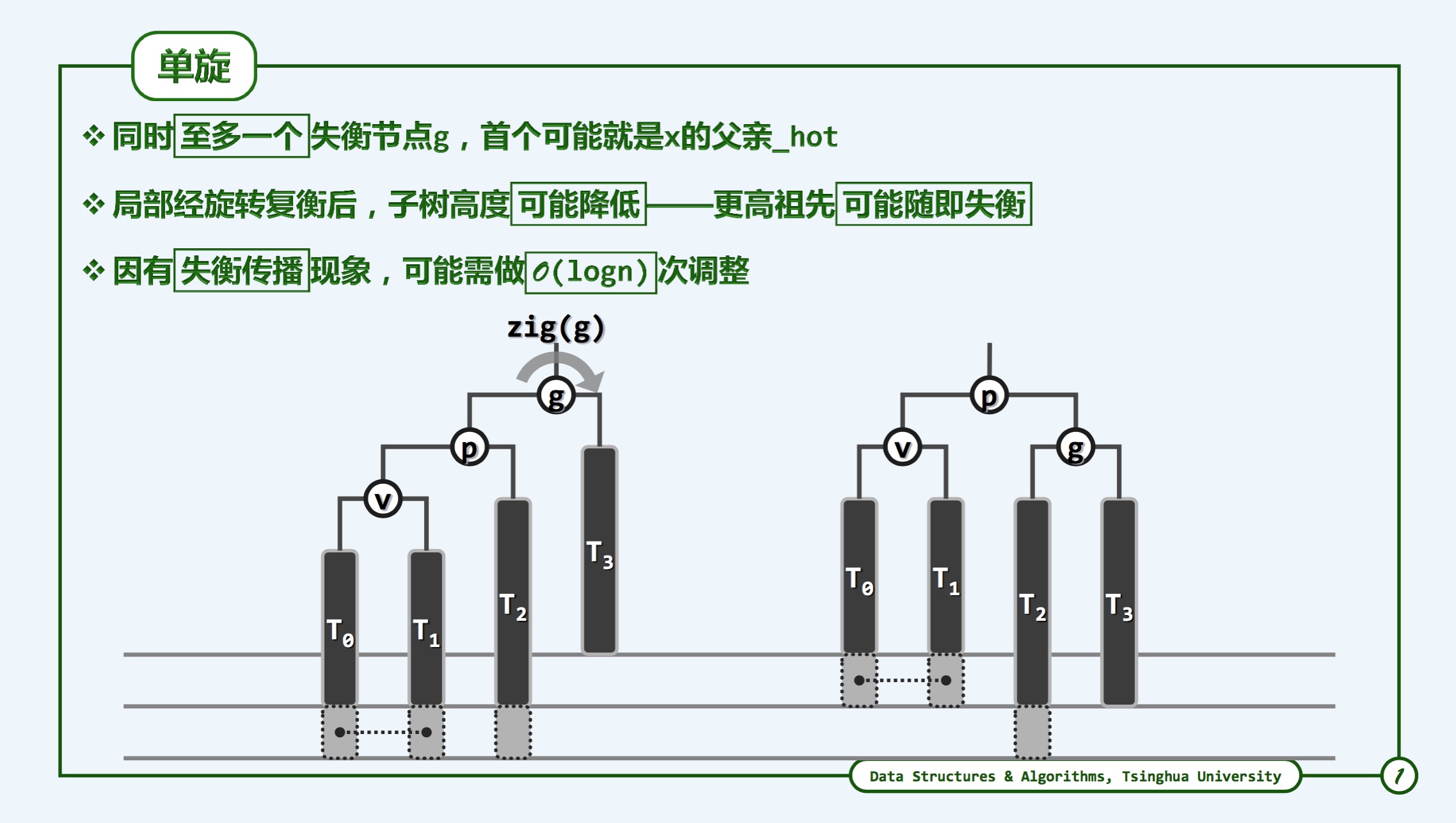
• 单旋转
  
  俩种单旋转：
• （向）右旋转——zig, （向）左旋转--zag
  • 如果导致失衡，插入一定插入在较高的子树，平衡因子由原来的+1变为+2。

           ┌────────────────────┐                               ┌────────────────────┐
           │balfactor: +1 -> +2 │                               │balfactor: +2 -> +1 │
           └────────────────────┘                               └────────────────────┘
┌────┐                .─.                                                  .─.
│ g  │──────────────▶(50 )                                                (40 )
└────┘               ▪`─'▪                                                ▪`─'▪
                   ▪       ▪            ─────────────────────▶          ▪       ▪
┌────┐         .─▪           ▪.─.                                  .─.▪           ▪.─.
│ p  │───────▶(40 )          (60 )                                (35 )           (50 )
└────┘       ▪ `─'▪           `─'                                 ▪`─'            ▪`─'▪
            ▪      ▪                                             ▪               ▪     ▪
┌────┐   .─▪       .▪.          ┌───────────────────┐           ▪               ▪       ▪
│ v  │─▶(35 )     (45 )◀────────│   may not exist   │         .─.            .─.          .─.
└────┘  ▫`─'       `─'          └───────────────────┘        (35 )          (45 )        (60 )
       ▫                                                      `─'            `─'          `─'
      ▫
   .─.      ┌──────────────────────┐
  (30 )◀────│ the new insert node  │
   `─'      └──────────────────────┘

操作步骤：

1. 首先得到一个临时的引用rc指向p
2. g的左子树指向p的右子树
3. 令g称为p的右孩子
4. 将局部子树的根指向p，然后去掉rc
5. zag左旋操作与此同理。

总的来说，单旋转呈现这么一种特性，即v，p，g分布单向，g为局部子树的根，调整完毕后，v，p，g自己可以形成

一个满树，p为局部子树的根

• 双旋转
• 此时v，p，g不再呈现一边的趋势，而是分开了。只需要执行一次zag左旋就可以达到之前的单旋转状态

           ┌────────────────────┐                               ┌────────────────────┐
           │balfactor: +1 -> +2 │                               │balfactor: +2 -> +1 │
           └────────────────────┘                               └────────────────────┘
┌────┐                .─.                                                  .─.
│ g  │──────────────▶(50 )                                           g->  (50 )
└────┘               ▪`─'▪                                                ▪`─'▪
                   ▪       ▪            ─────────────────────▶          ▪       ▪
┌────┐         .─▪           ▪.─.                                  .─.▪           ▪.─.
│ p  │───────▶(40 )          (60 )                         p->    (45 )           (60 )
└────┘       ▪ `─'▪           `─'                                 ▪`─'▪            `─'
            ▪      ▪                                             ▪     ▪
         .─▪       .▪.                                          ▪       ▪
        (35 ) ┌──▶(45 )                                       .─.       .─.
         `─'  │    `─'▪                                  v-> (40 )     (48 )
              │       ▪                                      ▪`─'       `─'
              │       ▪                                      ▪
       ┌────┐ │      .─.        ┌──────────────────────┐     .─.
       │ v  ├─┘     (48 )◀──────│ the new insert node  │    (35 )
       └────┘        `─'        └──────────────────────┘     `─'

1. 使用rc临时引用指向v
2. 让p的右子树指向v的左子树，
3. 让v的左子树指向p
4. 让局部子树的根指向v，并去掉rc
5. 就得到可以进行单旋的状态。

让我们再次来复习下右旋。

1. 让临时引用rc指向p
2. 让g的左子树指向p的右子树
3. 让p的右子树指向g
4. 让局部子树的根指向p，并去掉rc

到此，俩类共4个旋转操作的文字说明和图示如上。接下来，看到底怎样使用基本操作将树由BST拉回BBST

具体的四种旋转，可以查看AVL的四种旋转

AVL树

AVL树是BBST的一个种类。

平衡因子：左子树的高度减去右子树的高度,

AVL树的平衡因子不会超过1。 AVL树| balFac(v) | <= 1

回忆：之前我们定义过，空树的高度为-1，有一个节点的树高度为0。

一颗树的高度，就是树中深度最大节点的深度。

可以将状态定义如下

#define BalFac(x) (stature((x).lc) - stature((x).rc)) //平衡因子
#define AvlBalanced(x) ((-2 < BalFac(x)) && (BalFac(x) < 2)) //AVL平衡条件

失衡

插入

插入一个新节点，会导致节点的所有祖先失衡。 最多logN个节点。

• 原因：插入一个新节点，会更新节点以及节点所有祖先。
• 但是插入操作反而比删除操作更为简便一些。经过一次调整就可以完成
• 特征
  • 插入一个节点后，失衡节点集为新插入节点x的祖先，且高度均不低于新插入节点x的祖父。
  • 这个高度最低的失衡节点我们标记为g
    • g不一定是x的祖父，有可能是更高的祖先

插入重平衡

• 在x和g的通路上，我们设p为g的孩子，设置v为p的孩子。

实现：

1. 找g节点：那么重平衡的关键就是首先要找到g，这个很简单，从x的parent的往上开始，找不满足avl平衡条件
   
   的节点。
2. 找p，v节点：找到g节点后，我们知道g节点是失衡的，因为新插入了x节点，那么其在通往x节点的通路上的高度
   
   则会均大于他们的兄弟，借此，可以寻找p，v节点。其实就是找v节点就够了。p是v的parent。
   
   宏代码如下所示，解读：

#define tallerChild(x) (\ /*说白了就是在找高度更高的孩子*
        stature((x)->lc) > stature((x)->rc) ? (x)->lc : ( /*左高*/ \
        stature((x)->lc) < stature((x)->rc) ? (x)->rc : ( /*右高*/ \
        IsLchild(*(x)) ? (x)->lc : (x)->rc /*等高*/ \
        )\
        )\
        )\

等高情况发生在AVL树删除的情况下, 在插入情况下不会发生。

代码如下

void insert(const T &e)
{
// 插入操作前面的代码和正常BST的插入一样
    BinNodePos(T) & x = search(e);
    if(x)
        return ; // 目前不考虑重复元素
    x = new BinNode(e, _hot); // 直接完成新节点的构建，paret指向_hot，回想之前search的语义
    ++_size;
    BinNodePos(T) xx = x; // 接下来就是AVL树自己独有的部分

    /* ------- AVL 特有部分-------- */
    for(BinNodePos(T) g = xx->parent; g; g = g->parent)
    {
        if(!AvlBalanced(g)) // 根据g的定义找到g
        {
            // fromparentto返回当前节点父亲节点的指针域, 即局部子树的根引用
            // 由此可推断，rotate返回的是p
            FromParentTo(*g) = rotateAt(tallerChild( tallerChild(g) ));
            break;
        }
        else{
            updateHeightAbove(g); // 同时还要一步一步进行高度更新。但调整完毕后就直接退出了，
            // 不需要更新了, 原因在于插入调整不会改变g的祖先的高度, 和插入前的高度保持一致
        }
    }
    return xx;
}

效率：

可以看出，插入操作只需要执行O(logN)的查找时间，然后进行最多不超过O(logN)的平衡确认，如果失衡

执行不超过2次的旋转调整，由此AVL树的插入操作在O(logN)的时间内可以完成

删除

删除一个新节点，只会导致最多1个节点失衡。

• 原因：如果导致失衡，删除节点时，一定是删除更短的那个分支，而这个子树的高度担当还是在最长
  
  子树那里。
• 特征
  • 与插入不同的是，删除操作中失衡节点集始终最多只含有一个节点。
• 重平衡 教材P198页有详细讲解，这标记一下
  • 寻找g：节点依然是按照之前的方法，通过被删除节点的parent向上查找，到不满足AVL平衡条件的那个
    
    点
  • 寻找p：作为失衡节点，其另一边的高度至少为1才能构成失衡。因此必定有一个非空的孩子p，且是
    
    tallerchild
  • 寻找v：寻找v的时候，p的俩个孩子高度可能相等。此时我们优先选取和p同向者，单旋当然比双
    
    旋简单。

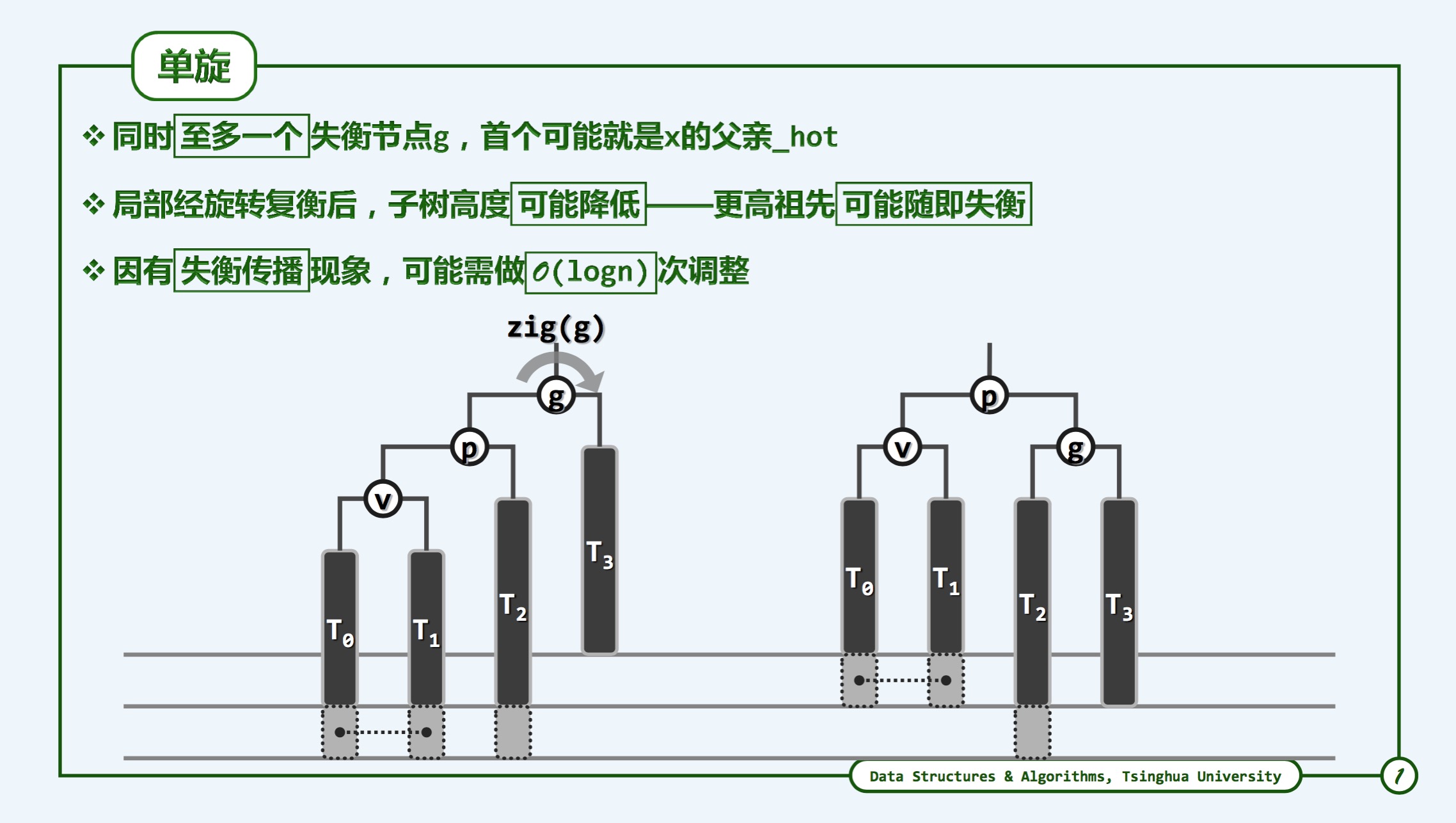
图片转自邓老师pdf，侵权必删

• Q：就图中而言，为什么v的T1, T0俩个后辈一定存在？
  • A：如果v下面的俩个后辈不存在，而T2的后辈存在，那么此时T2高度更高，自然选取T2为v

实现代码如下

bool remove(const T &e)
{
    /* ----- BST 删除操作(缺少一个高度更新，在AVL中更新) ----- */
    BinNodePos(T) x = search(e);
    if(!x)
        return false; // 删除元素必须保证存在
    BST<T>::removeAt(x, _hot);
    --_size;
    /* ----- AVL 删除所特有的 ----- */
    for(BinNodePos(T) g = _hot; g; g = g->parent)
    {
        if(!AvlBalanced(*g)) // 如果不满足avl平衡条件
        {
            g = FromParentTo (*g) = rotateAt(tallerChild(tallerChild(g)));
            updateHeight(g);
        }
    }
    return true;
}

这里简单回忆下removeAt操作

void removeAt(bnp &x, bnp &hot)
{
    bnp w = x;
    bnp succ = nullptr;
    if(!HasLc(x))
        succ = x = x->rc;
    if(!HasRc(x))
        succ = x = x->lc;
    else{
        w = w->succ();
        swap(x->data, w->data);
        bnp u = w->parent;
        ((u == x) ? u->rc : u->lc) = succ = w->rc;
    }
    hot = w->parent;
    //release(w->data);
    if(succ) succ->parent = hot;
    delete(w);
    return  succ;
}

失衡传播:

经过一次删除调整后，原先子树的高度有可能不变，有可能减一。如果发生了减一，那么就相当于从被删除节点

的父亲开始，每次都需要进行AVL平衡条件的检查，一直到树的根部。

树的真正调整

虽然我们已经学习了基本变换，但是我们并不适用，而是仅仅让其帮助我们理解，我们所仍然采用的方式

叫做3+4重构，直接将树的g, p, v拆开，按照a < b < c的方式重新命名，同时其下面的四颗子树也按照

T0 < T1 < T2 < T3 的方式重新命名。最终的状态会达到

T0 < a < T1 < b(root) < T2 < c < T3 的状态

3+4重构在这里非常简洁，所以重点还是这里的rotateAt

template <typename T>
BinNodePos(T)
BST<T>::connect34( // 3+4 重构
        BinNodePos(T) a, BinNodePos(T) b, BinNodePos(T) c,
        BinNodePos(T) T0, BinNodePos(T) T1, BinNodePos(T) T2, BinNodePos(T) T3)
{
    a->lc = T0;     if(T0)  T0->parent = a;
    a->rc = T1;     if(T1)  T1->parent = a;
    updateHeight(a);
    c->lc = T2;     if(T2)  T2->parent = c;
    c->rc = T3;     if(T3)  T3->parent = c;
    updateHeight(c);
    b->lc = a;      a->parent = b;
    b->rc = b;      c->parent = b;
    updateHeight(b);
    return b;
}

// 根据我们之前讨论的四种旋转情况，在不同情况下进行a, b, c 以及T0, T1, T2, T3的排序
template <typename T>
BinNodePos(T)
BST<T>::rotateAt(BinNodePos(T) v) // 传入参数为孙子节点v
{
    BinNodePos(T) g, p;
    p = v->parent;
    g = p->parent;
    if(IsLChild(*p))
    {
        if(IsLChild(*v))
        {
            p->parent = g->parent; // 向上连接
            return connect34(v, p, g, v->lc, v->rc, p->rc, g->rc);
        }
        else{
            v->parent = g->parent;
            return connect34(p, v, g, p->lc, v->lc, v->rc, g->rc);
        }
    }
    else{
        if(IsLChild(*v))
        {
            v->parent = g->parent;
            return connect34(g, v, p, g->lc, v->lc, v->rc, p->rc);
        }
        else{
            p->parent = g->parent;
            return connect34(g, p, v, g->lc, p->lc, v->lc, v->rc);
        }
    }
}

综合评价

AVL树优点：查找，插入，删除均为O(logN)时间复杂度，O(N)的空间

AVL树缺点：

1. 需要借助高度或平衡因子，需要改造元素结构，或额外封装，过于做作
2. 实测和理论尚有差距
3. 最重要的因子，删除操作后，会经过一次旋转调整，但有可能导致整个局部的树高度比未删除之前减1，因此会再次出发调整，最
   
   坏情况下全树需要做logN次调整, 变化量过于大