最小费用最大流模板洛谷P3381

题目描述

如题，给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含四个正整数ui、vi、wi、fi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi），单位流量的费用为fi。

输出格式：

一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。

输入输出样例

输入样例#1：复制

输出样例#1：复制

50 280

说明

时空限制：1000ms,128M

（BYX：最后两个点改成了1200ms）

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=1000，M<=1000

对于100%的数据：N<=5000，M<=50000

样例说明：

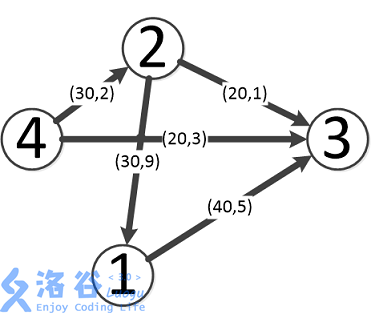
如图，最优方案如下：

第一条流为4-->3，流量为20，费用为3*20=60。

第二条流为4-->2-->3，流量为20，费用为（2+1）*20=60。

第三条流为4-->2-->1-->3，流量为10，费用为（2+9+5）*10=160。

故最大流量为50，在此状况下最小费用为60+60+160=280。

故输出50 280。

#include<bits/stdc++.h>

using namespace std;

const int MAXN=50001;

const int INF=0x3f3f3f3f;

struct Edge{

    int from,to,cap,flow,cost;

    Edge(int u,int v, int c,int f ,int w):from(u),to(v),cap(c),flow(f),cost(w)

    {}

};

struct MCMF

{

    int n,m;

    vector<Edge>edges;

    vector<int>G[MAXN];

    int inq[MAXN];

    int d[MAXN];

    int p[MAXN];

    int a[MAXN];

    void init(int n) {

        this->n=n;

        for (int i=0;i<=n;i++)G[i].clear();

        edges.clear();

    }

    void AddEdge(int from, int to,int cap,int cost)

    {

        edges.push_back(Edge(from,to,cap,0,cost));

        edges.push_back(Edge(to,from,0,0,-cost));

        m=edges.size();

        G[from].push_back(m-2);

        G[to].push_back(m-1);

    }

    bool BellmanFord(int s,int t,int &flow,long long &cost){

        for(int i=0;i<=n;i++)d[i]=INT_MAX;

        memset(inq,0, sizeof(inq));

        d[s]=0;inq[s]=1;p[s]=0;a[s]=INT_MAX;

        queue<int >Q;

        Q.push(s);

        while(!Q.empty()){

            int u=Q.front();Q.pop();

            inq[u]=0;

            int ll=G[u].size();

            for (int i = 0; i <ll ; ++i) {

                Edge& e=edges[G[u][i]];

                if(e.cap>e.flow&&d[e.to]>d[u]+e.cost){

                    d[e.to]=d[u]+e.cost;

                    p[e.to]=G[u][i];

                    a[e.to]=min(a[u],e.cap-e.flow);

                    if(!inq[e.to]){Q.push(e.to);inq[e.to]=1;}

                }

            }

        }

        if(d[t]==INT_MAX) return false;

        flow+=a[t];

        cost+=(long long)d[t]*(long long )a[t];

        for (int u = t; u !=s ; u=edges[p[u]].from) {

            edges[p[u]].flow+=a[t];

            edges[p[u]^1].flow-=a[t];

        }

        return true;

    }

    int MincostMaxflow(int s,int t,long long &cost){

        int flow=0;cost=0;

        while(BellmanFord(s, t, flow, cost));

        return flow;

    }

};

int main()

{

    int n,m,s,t;

    scanf("%d%d%d%d",&n,&m,&s,&t);

    int u,v,f,w;

    MCMF M;

    M.init(n);

    for (int i = 0; i <m ; ++i) {

        scanf("%d%d%d%d",&u,&v,&f,&w);

        M.AddEdge(u,v,f,w);

    }

    long long cost=0;

    long long ans=M.MincostMaxflow(s,t,cost);

    printf("%lld %lld\n",ans,cost);

    return 0;

}