Logistic regression中regularization失败的解决方法探索（文末附解决后code）

在matlab中做Regularized logistic regression

原理：

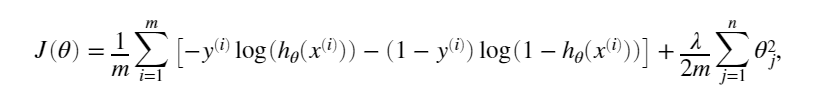
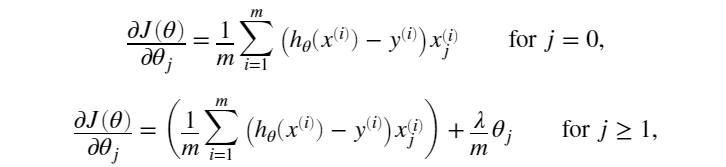
我的代码：

function [J, grad] = costFunctionReg(theta, X, y, lambda)
%COSTFUNCTIONREG Compute cost and gradient for logistic regression with regularization
%   J = COSTFUNCTIONREG(theta, X, y, lambda) computes the cost of using
%   theta as the parameter for regularized logistic regression and the
%   gradient of the cost w.r.t. to the parameters. 

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly
J = 0;
grad = zeros(size(theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta

    h = sigmoid(X*theta);
    theta2=[0;theta(2:end)];

    J_partial = sum((-y).*log(h)+(y-1).*log(1-h))./m;
    J_regularization= (lambda/(2*m)).*sum(theta2.^2);
    J = J_partial+J_regularization;

    grad_partial = sum((h-y).*X)/m;
    grad_regularization = lambda.*theta2./m;
    grad = grad_partial+grad_regularization;

% =============================================================

end

运行结果：

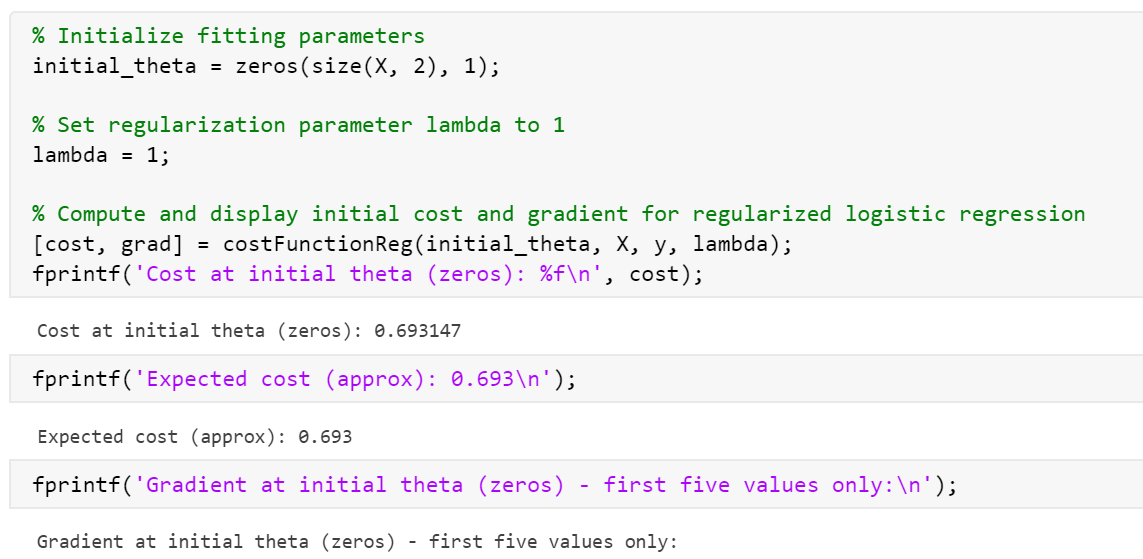
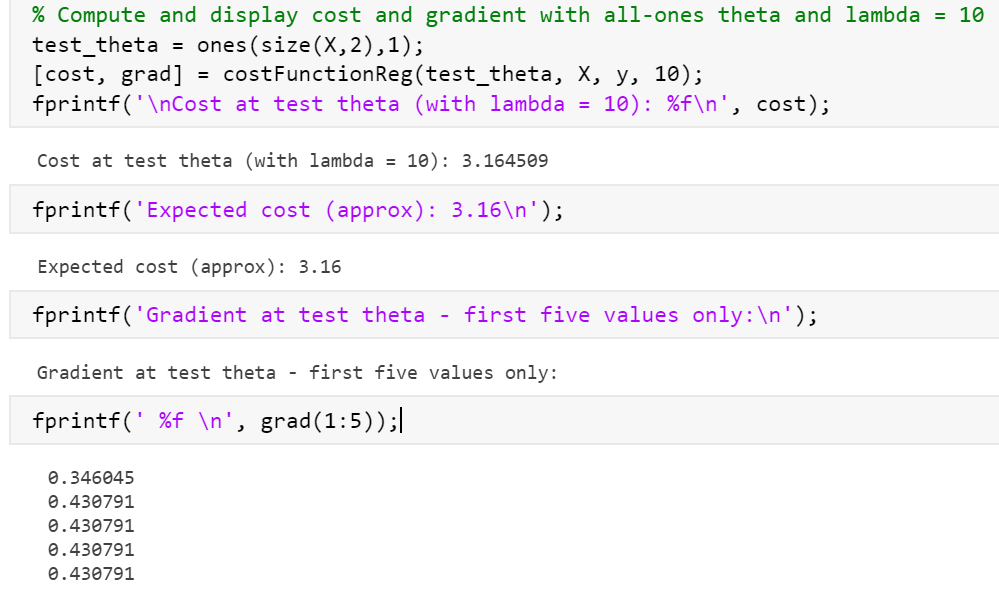
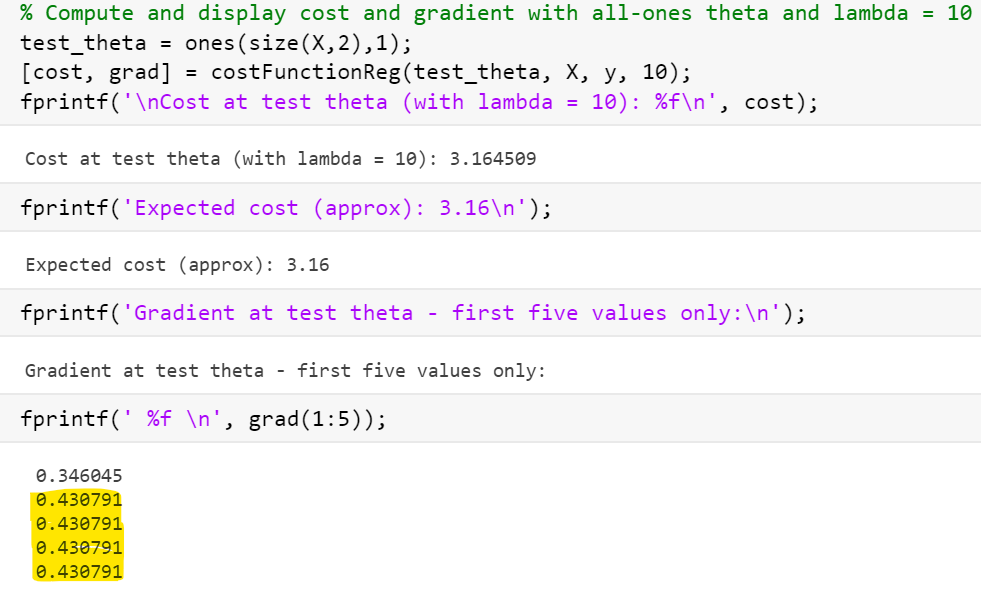
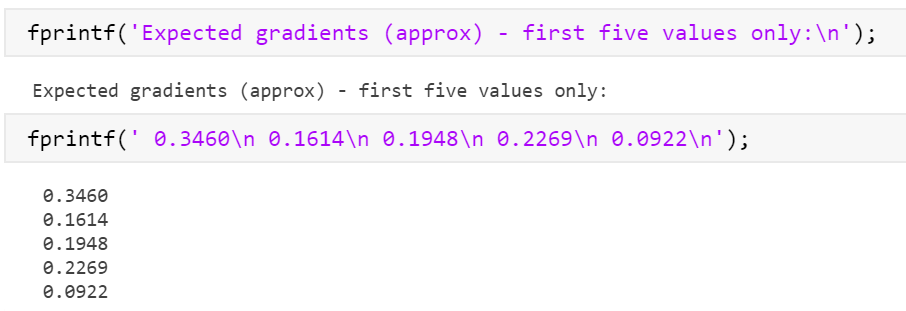
标黄的与下面的预期对比发现不同

尝试删去

+grad_regularization

.rtcContent { padding: 30px }
.lineNode { font-size: 10pt; font-family: Menlo, Monaco, Consolas, "Courier New", monospace; font-style: normal; font-weight: normal }

部分结果符合预期，部分不符合

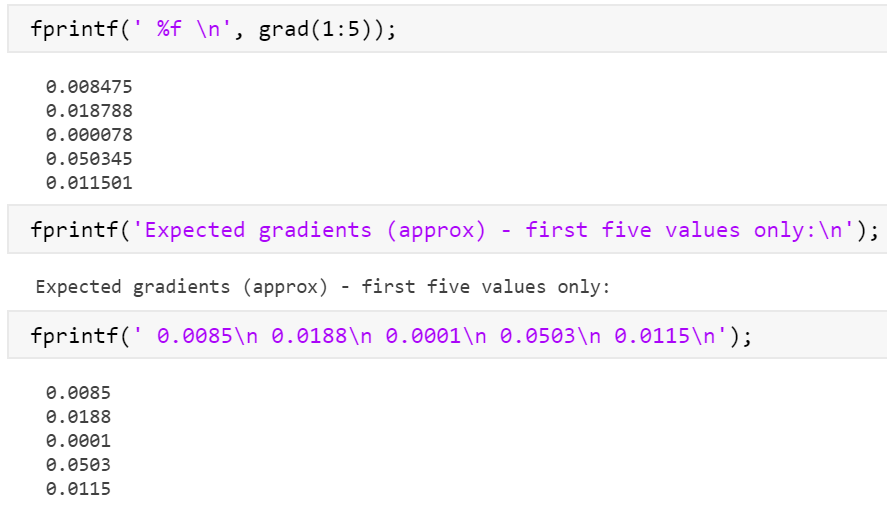
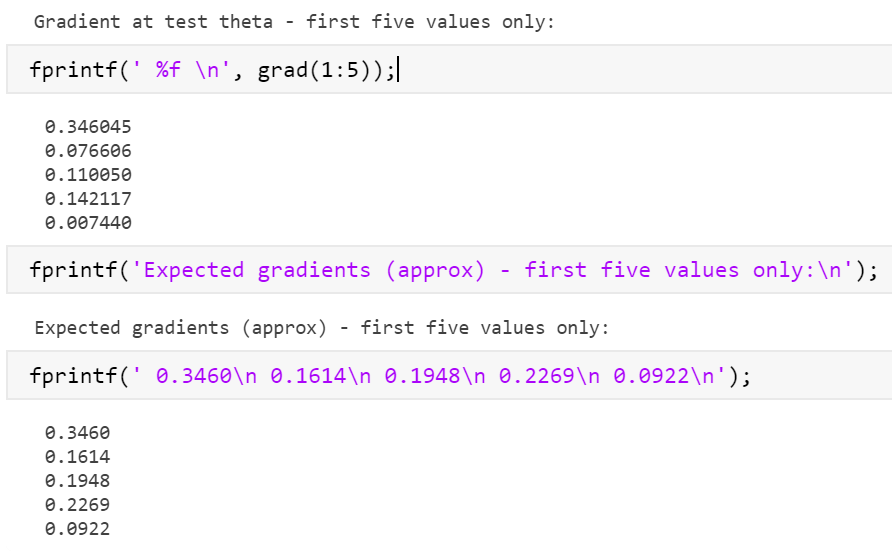
尝试大佬代码

%Hypotheses
hx = sigmoid(X * theta);
%%The cost without regularization
J_partial = (-y' * log(hx) - (1 - y)' * log(1 - hx)) ./ m;
%%Regularization Cost Added
J_regularization = (lambda/(2*m)) * sum(theta(2:end).^2);
%%Cost when we add regularization
J = J_partial + J_regularization;
%Grad without regularization
grad_partial = (1/m) * (X' * (hx -y));
%%Grad Cost Added
grad_regularization = (lambda/m) .* theta(2:end);
grad_regularization = [0; grad_regularization];
grad = grad_partial + grad_regularization;

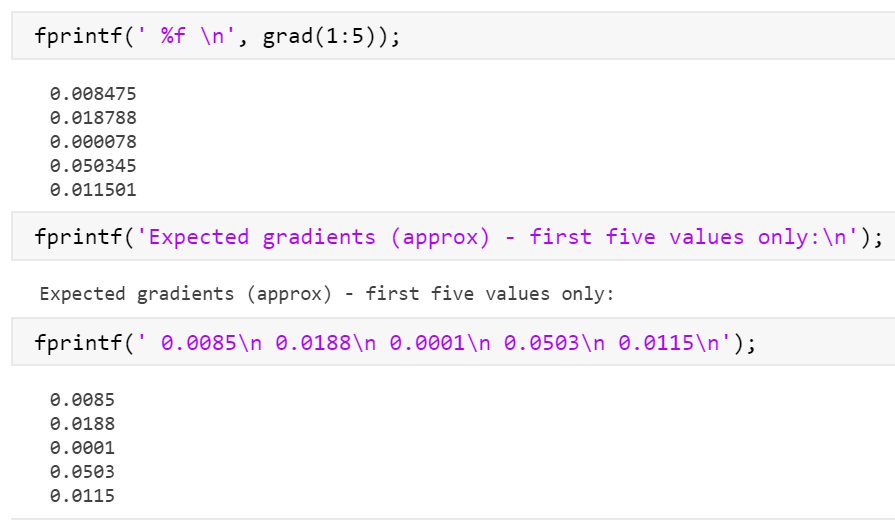
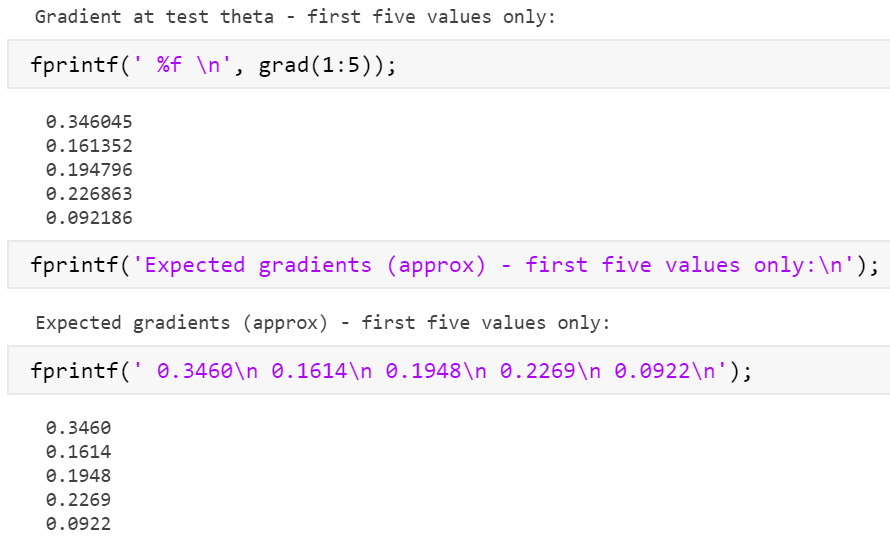
完全成功！？我不李姐……

观察大佬代码发现，我和大佬的区别在于：

最开始的theta向量和计算J(theta)和grad时候使用sum的数目

故尝试修改和大佬数目一样多的sum

    h = sigmoid(X*theta);
    theta2=[0;theta(2:end)];

    J_partial = (-y).*log(h)+(y-1).*log(1-h)./m;
    J_regularization= (lambda/(2*m)).*sum(theta2.^2);
    J = J_partial+J_regularization;

    grad_partial = (h-y).*X/m;
    grad_regularization = lambda.*theta2./m;
    grad = grad_partial+grad_regularization;

结果：incompatible不兼容

文档对该错误的解释如下

事已至此，只好向大佬更近一步！

    h = sigmoid(X*theta);

    J_partial = (-y).*log(h)+(y-1).*log(1-h)./m;
    J_regularization= (lambda/(2*m)).*sum(theta(2:end).^2);
    J = J_partial+J_regularization;

    grad_partial = (h-y).*X/m;
    grad_regularization = lambda.*theta(2:end)./m;
    grad_regularization2=[0;grad_regularization];

    grad = grad_partial+grad_regularization2;

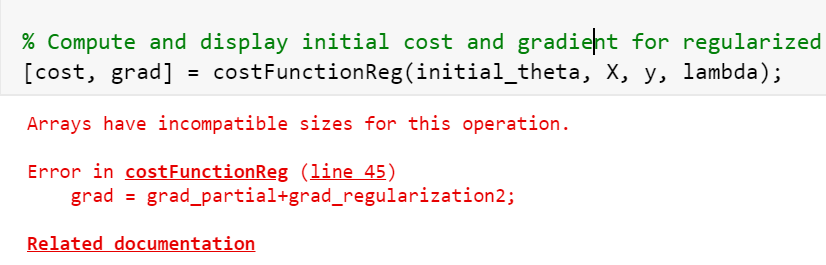
为什么还是不兼容？

到底哪里出了问题？

最后，尝试离大佬更近一步，把grad_partial里的(h-y).*X/m变成了(1/m) * (X' * (h -y))

    h = sigmoid(X*theta);

    J_partial = (1/m).*((-y).*log(h)+(y-1).*log(1-h));
    J_regularization= (lambda/(2*m)).*sum(theta(2:end).^2);
    J = J_partial+J_regularization;

    grad_partial = (1/m) * (X' * (h -y));
    grad_regularization = (lambda/m).*theta(2:end);
    grad_regularization = [0; grad_regularization];
    grad = grad_partial+ grad_regularization;

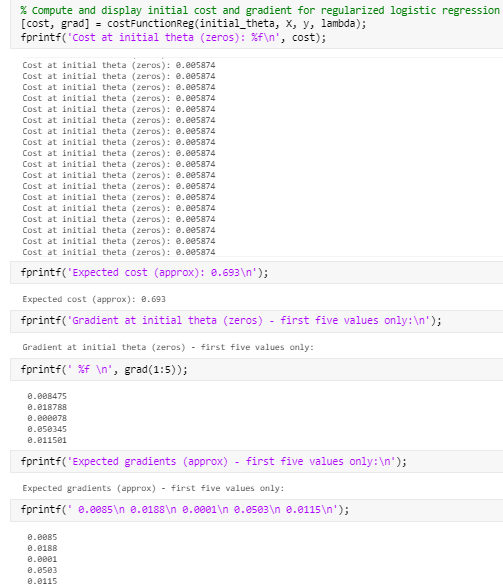
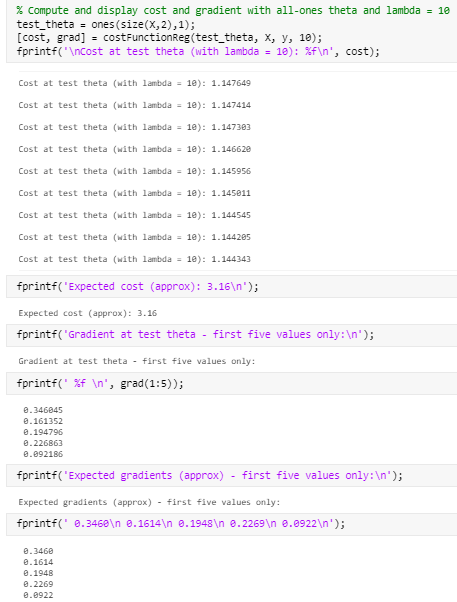
舒服了！

但，等等，上面怎么那么多行，数值还不对？看来不能完全靠大佬，还得自己改！！！

    h = sigmoid(X*theta);

    J_partial = (1/m).*sum((-y).*log(h)+(y-1).*log(1-h));
    J_regularization= (lambda/(2*m)).*sum(theta(2:end).^2);
    J = J_partial+J_regularization;

    grad_partial = (1/m) * (X' * (h -y));
    grad_regularization = (lambda/m).*theta(2:end);
    grad_regularization = [0; grad_regularization];
    grad = grad_partial+ grad_regularization;

最终，得到了满意的答案

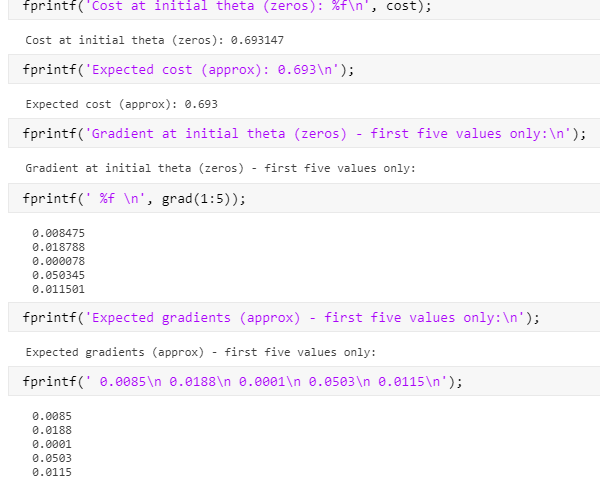
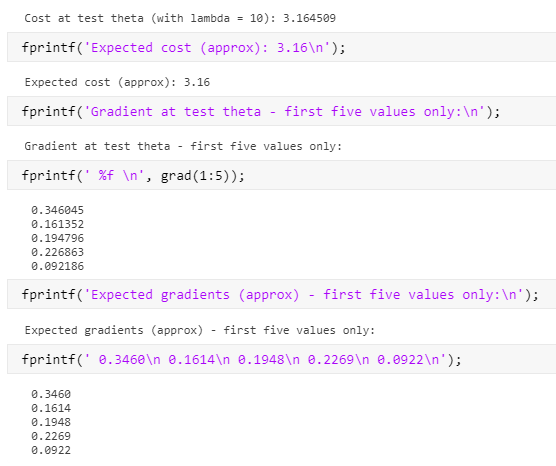
以及

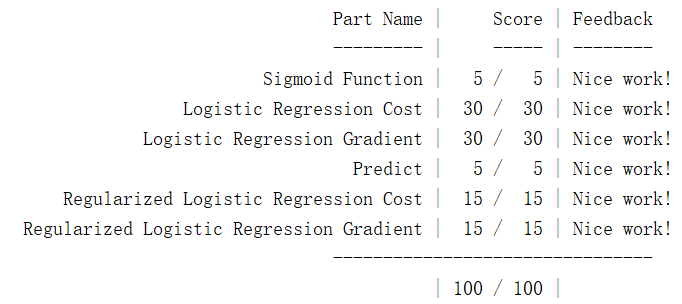
 总结一下出现的问题

01不兼容，就像上面说明的那样，行列不匹配

（解决方法：查看有无sum、是值还是array，把系数往前放，修改两数相乘的顺序）

02加入grad_regularization后，grad(1,5)的后四项都出现了问题（很神奇地值相等），

一旦去掉又与正确值有小范围差距（缺少grad_regularization导致的）

说明grad_regularization存在问题

而如果一开始就将theta变为第一行元素是0的矩阵，很容易出现不兼容的问题

大佬的代码提示我们特殊情况可以分出来特殊处理，也就是：

在计算J(θ)不使用矩阵，而是用除0外、后面的θ直接产出需要的值

在计算grad时，由于输出也是矩阵，所以可以创建一个含0和其他θ的矩阵

这样既可以避免不兼容，也可以得出正确的结果

最终的部分code如下

    h = sigmoid(X*theta);

    J_partial = (1/m).*sum((-y).*log(h)+(y-1).*log(1-h));
    J_regularization= (lambda/(2*m)).*sum(theta(2:end).^2);
    J = J_partial+J_regularization;

    grad_partial = (1/m) * (X' * (h -y));
    grad_regularization = (lambda/m).*theta(2:end);
    grad_regularization = [0; grad_regularization];
    grad = grad_partial+ grad_regularization;