吴恩达老师机器学习课程chapter09——异常检测

本文是非计算机专业新手的自学笔记，高手勿喷。

本文仅作速查备忘之用，对应吴恩达(AndrewNg)老师的机器学期课程第十五章。

吴恩达老师机器学习课程chapter09——异常检测

异常检测指的是用来判断样本是否异常的过程。

一元高斯分布/正态分布

对于随机变量$x \in \mathbb{R}$，服从一个数学期望为μ、方差为σ^2的正态分布，记为 $N(μ，σ^{2})$，如下：

\[\begin{array}{l}
N(μ，σ^{2})=p\left(x ; \mu, \sigma^{2}\right) =\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)
\end{array}
\]

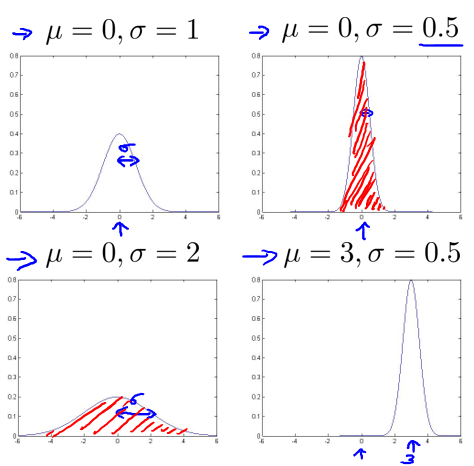
μ影响函数分布中心位置；σ^2越大函数越平。

从样本中计算数学期望为μ、方差为σ^2：

\[\mu=\frac{1}{m} \sum_{i=1}^{m} x^{(i)}\\
\sigma^{2}=\frac{1}{m} \sum_{i=1}^{m} {\left(x^{(i)}-\mu\right)^{2}}
\]

异常检测算法

有训练集$ x^{(1)}, x^{(2)} \cdots x^{(m)} $,认为各样本独立同分布，有：

\[p(x)=p\left(x_{1} ; \mu_{1}, \sigma_{1}^{2}\right) p\left(x_{2} ; \mu_{2}, \sigma_{2}^{2}\right) p\left(x_{3} ; \mu_{3}, \sigma_{3}^{2}\right) \cdots p\left(x_{n} ; \mu_{n}, \sigma_{n}^{2}\right)
=\prod_{j=1}^{n} p\left(x_{j} ; \mu_{j}, \sigma_{j}^{2}\right)
\]

有异常检测算法如下：

以二维空间为例，可视化之后的直观表现如下：

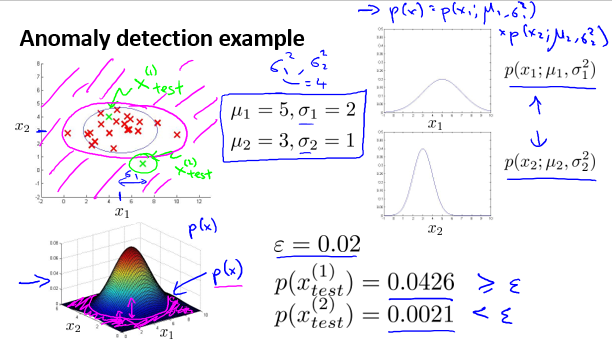
异常检测设计

给定有标签的样本，可以按照一定比例将其分为训练集、交叉验证集、测试集，一般比例可以选择6:2:2。

例如:

设计步骤如下：

如何选择 $\varepsilon $

可以通过设定不同的 $\varepsilon $, 在交叉验证集上考察其F1Score，选择F1Score最高时对应的$\varepsilon $。

如何选择特征

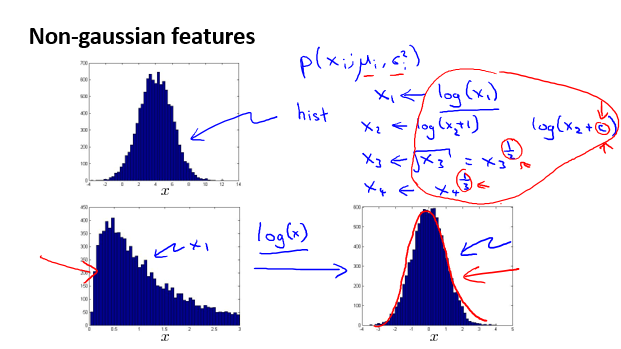
实际操作中，选择接近高斯分布的特征；

如果特征与高斯分布相差很远，可以使用对数函数、幂函数，将特征转变为与高斯分布相近的新特征。

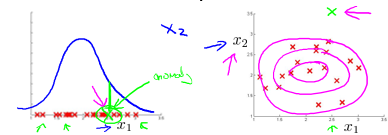
当现有特征不能将异常与非异常的样本区分时，应该寻找新的特征将异常样本剥离出来。

与监督学习的区别

异常检测与监督学习有如下区别：

监督学习通常拥有大量样本，当中包含了许多正样本与负样本；而异常检测中正样本数量通常很少，负样本数量很多。

监督学习中，正样本通常拥有明显的特征，正样本之间很类似；而异常检测中正样本之间可能差异很大，可能会出现从未见过的类型。

多元高斯分布

当特征之间的独立性不够明显，会出现异常样本被淹没的情况：

这时候需要引入协方差矩阵 $\Sigma$ 。对于一组样本， $\mu \in \mathbb{R}^{n}, \Sigma \in \mathbb{R}^{n \times n}$，其高斯分布如下：

\[p(x ; \mu, \Sigma)=
\frac{1}{(2 \pi)^{\frac{}{2}}|\varepsilon|^{\frac{1}{2}}}
\exp \left(-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)\right)
\]

其中，均值向量 $\mu$ 对分布的影响如下：

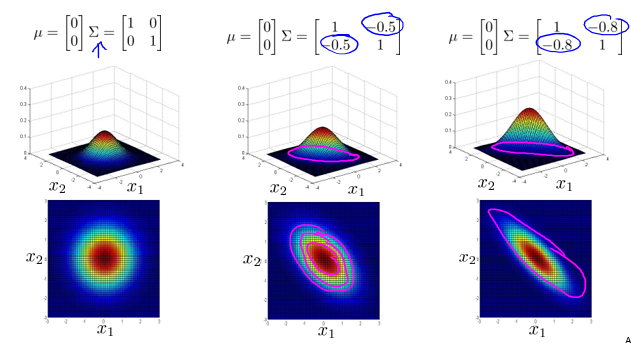
协方差矩阵 $\Sigma $对分布的影响如下：

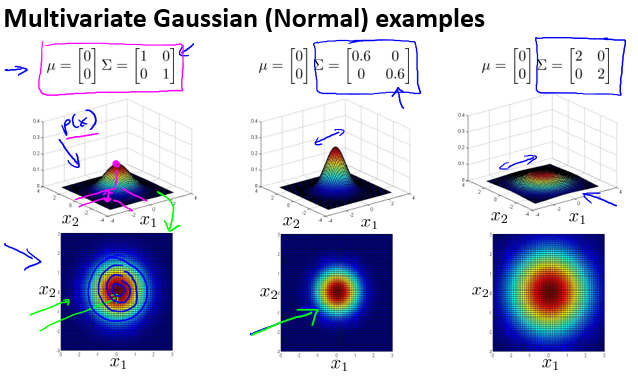
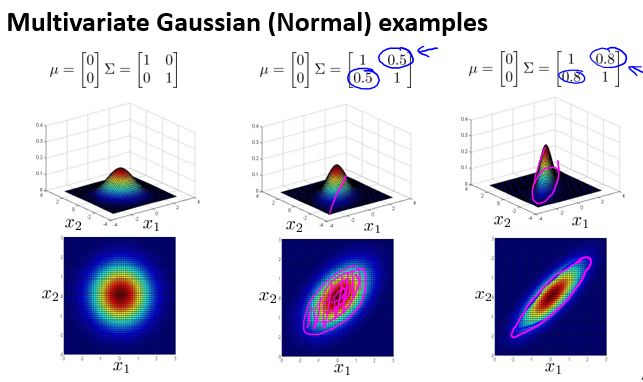
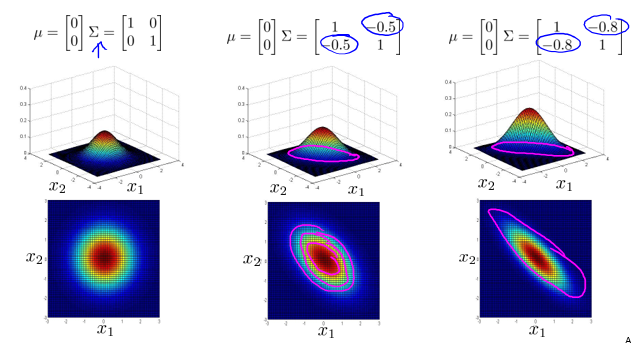
当$\Sigma$满足如下条件时：

\[\Sigma=
\begin{bmatrix}
\sigma_{1}^{2} &0 &\cdots &0 \\
0& \sigma_{2}^{2} &\cdots &0 \\
\vdots &\vdots & \ddots &\vdots \\
0& 0 & \cdots &\sigma_{n}^{2}
\end{bmatrix}
\]

多元高斯分布与一元高斯分布的乘积是一样的（各特征独立）。

引入多元高斯分布之后，异常检测算法也要做出如下修改：

多元高斯分布方法与一元高斯分布方法的比较：