用t-SNE进行流形学习（digits数据集）

流行学习算法：

• 是一类用于可视化的算法，它允许进行更复杂的映射，通常也可以给出更好的可视化。
• t-SNE算法是其中一种。

PCA是用于变换数据的首选方法，也可以进行可视化，但它的性质（先旋转然后减少方向）限制了有效性。因此，我们可以使用流形学习算法进行数据可视化。

1、什么是t-SNE

t-SNE算法：

• 主要思想：找到数据的一种二维表示，尽可能保持数据点之间的距离（高内聚，低耦合）。

  • 这种方法不知道类别标签，是完全无监督的。

  • 它只能变换用于训练的数据，不支持新数据（没有transform方法），即不能用于测试集。

  • 具有调节参数（perplexity、early_exaggeration），通常默认参数的效果就很好。

2、将t-SNE应用于手写数字数据集

（1）了解一下digits数据集

  from sklearn.datasets import load_digits
  from matplotlib import pyplot as plt
  from sklearn.decomposition import PCA
  from sklearn.model_selection import train_test_split
  import numpy as np

  digits = load_digits()

  fig,axes = plt.subplots(2,5,figsize=(10,5),subplot_kw={'xticks':(),'yticks':()})

  #展示前10张图片
  for ax,img in zip(axes.ravel(),digits.images):
      ax.imshow(img)

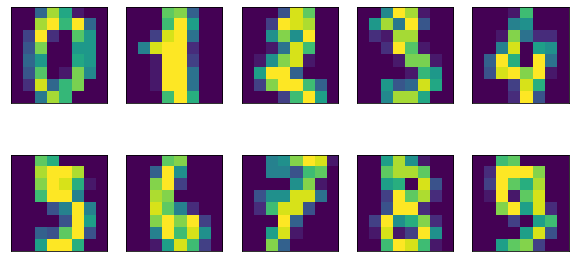
  print(digits.images.shape)
  print(digits.data.shape)
  print(digits.target_names.shape)

  输出：
  (1797, 8, 8)
  (1797, 64)
  (10,)

在这个数据集中，包含1797张8*8灰度的图像。每个数据点都是一个数字，共有10种类别（数字0~9）

（2）使用PAC作为一个对比

• 使用PCA将数据集将至二维，并将其可视化。对pca变换后的数据的前两个主成分作图

  pca = PCA(n_components=2)
  pca.fit(digits.data) #t-SNE只能用于训练集
  
  #将数据样本用pca进行转换
  digits_pca = pca.transform(digits.data)
  
  plt.figure(figsize=(10,10))
  plt.xlim(np.min(digits_pca[:,0]),np.max(digits_pca[:,0]))
  plt.ylim(np.min(digits_pca[:,1]),np.max(digits_pca[:,1]))
  
  #将数据点绘制成文本
  for i in range(len(digits.data)):
      plt.text(digits_pca[i,0],digits_pca[i,1],str(digits.target[i]))
  
  plt.xlabel("First Principal component")
  plt.ylabel("Second Principal cpmponent")
  

• 用pca可以将数据digits.data降到2维，没分别利用主成分1和主成分2，将数据点可视化至平面（只有两个特征才可作图到二维平面，便于观察）

• 利用pca前两个主成分可以把数字0,6,4相对较好地分开，但仍有重叠，其他大部分数字大量重叠。

（3）使用t-SNE

  from sklearn.manifold import TSNE

  tsne = TSNE(random_state=42)

  digits_tsne = tsne.fit_transform(digits.data)

  plt.figure(figsize=(10,10))
  plt.xlim(np.min(digits_tsne[:,0]),np.max(digits_tsne[:,0])+1)
  plt.ylim(np.min(digits_tsne[:,1]),np.max(digits_tsne[:,1])+1)

  #将数据点绘制成文本
  for i in range(len(digits.data)):
      plt.text(digits_tsne[i,0],digits_tsne[i,1],str(digits.target[i]))

  plt.xlabel("t-SNE feature 0")
  plt.ylabel("t-SNE feature 1")

• 可以发现t-SNEde结果很棒，所有的类别都被明确地分开，形成密集的组

• 找到数据的一种二维表示，仅根据原始空间中数据点之间的靠近程度就能将各个类别明确分开

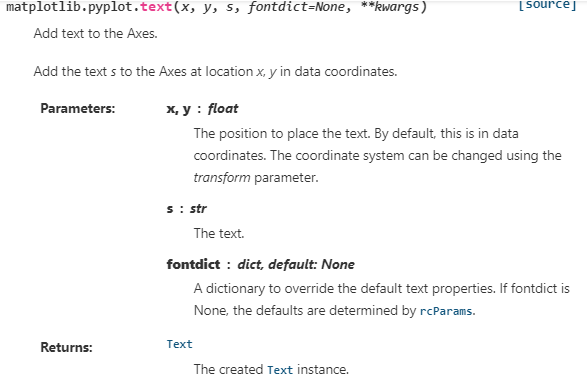
（4）关于matplotlib.pylot.text

在本次实验代码中，用到了plt.text（）方法将降维后的数据在二维平面上用文本画出。

• 用法详见plt.text官方文档

ps：

利用散点图也能可视化我们上述的二维数据，但是不直观，因为类别太多了。