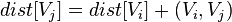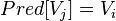Bellman-Ford算法及其队列优化(SPFA)
一、算法概述
Bellman-Ford算法解决的是一般情况下的单源最短路径问题。所谓单源最短路径问题:给定一个图G=(V,E),我们希望找到从给定源结点s属于V到每个结点v属于V的最短路径。单源最短路径问题可以用来解决许多其他问题,其中包括下面几个最短路径的变体问题。包括单目的最短路径问题、单结点最短路径问题、所有结点对最短路径问题,这里不详细介绍。回到bellman-Ford,在这里,边的权重可以为负值。给定带权重的有向图G=(V,E)和权重函数W
: E-->R,Bellman-Ford算法返回一个布尔值,以表明是否存在一个从源点可以到达的权重为负值的环路。如果存在这样的环路,算法将告诉我们不存在解决方案。如果没有这种环路存在,算法将给出最短路径和它们的权重。边的权值可以为负数、实现简单,缺点是时间复杂度过高,高达O(VE)。但算法可以进行若干种优化,提高了效率。
自然语言描述
对有向图 ,用贝尔曼-福特算法求以
,用贝尔曼-福特算法求以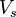 为源点的最短路径的过程:
为源点的最短路径的过程:
- 建立
 ,表示目前已知源点到各个节点的最短距离,起始值
,表示目前已知源点到各个节点的最短距离,起始值 ,其余皆为
,其余皆为 。
。 - 建立
 ,
, 表示某节点路径上的父节点,起始值皆为NULL。
表示某节点路径上的父节点,起始值皆为NULL。 - 对
 ,比较
,比较 和
和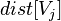 ,并将小的赋给
,并将小的赋给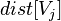 ,如果修改了
,如果修改了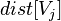 则
则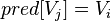 (松弛操作)
(松弛操作) - 重复以上操作
 次
次 - 再重复操作一次,如
 ,则此图存在负权环。
,则此图存在负权环。
伪代码表示
BellmanFord(G,s)
for i = 0 to n-1 do
dist[i]= ∞
Pred[i]= 0
dist[s]=0
for k = 1 to n-1 do
foreach∈
do
ifdo
foreach∈
do
ifdo
return "No Shortest Path"
return dist[]
二、原理
为什么说最短路径不存在负环呢?
如果图G包含从s可以达到的权重为负值的环路,则最短路径权重无定义。从s到该环路上的任意结点的路径都不可能是最短路径,因为我们只要沿着任何“最短”路径再遍历一次权重为负值的环路,则总是可以找到一条权重更小的路径。如果从结点s到结点v的某条路径上存在权重为负值的环路,我们定义s到v的最短路径等于负无穷。
松弛操作
它的原理是对图进行V-1次松弛操作,得到所有可能的最短路径。对于一条边(u,v)的松弛过程为:首先测试一下是否可以对源点s到v的最短路径进行改善。测试的方法是,将从结点s到结点u之间的最短路径距离加上结点u与v之间的权重,并与当前的s到v的最短路径估计进行比较,如果前者更小,则对v.d(源点s到v的最短路径) 和v.π(前驱结点)进行更新。
每次松弛操作实际上是对相邻节点的访问,第 次松弛操作保证了所有深度为n的路径最短。由于图的最短路径最长不会经过超过
次松弛操作保证了所有深度为n的路径最短。由于图的最短路径最长不会经过超过 条边,所以可知贝尔曼-福特算法所得为最短路径。
条边,所以可知贝尔曼-福特算法所得为最短路径。
负边权操作
与迪科斯彻算法不同的是,迪科斯彻算法的基本操作“拓展”是在深度上寻路,用于有向无环图的最短路径算法对每条边仅松弛一次。Bellman-Ford“松弛”操作则是在广度上寻路,这就确定了贝尔曼-福特算法可以对负边进行操作而不会影响结果。
负权环判定
因为负权环可以无限制的降低总花费,所以如果发现第 次操作仍可降低花销,就一定存在负权环。
次操作仍可降低花销,就一定存在负权环。
三、队列优化——SPFA
求单源最短路的SPFA算法的全称是:Shortest Path Faster Algorithm。松弛操作必定只会发生在最短路径前导节点松弛成功过的节点上,用一个队列记录松弛过的节点,可以避免了冗余计算。复杂度可以降低到O(kE),k是个比较小的系数(并且在绝大多数的图中,k<=2,然而在一些精心构造的图中可能会上升到很高)
参考:算法导论、http://zh.wikipedia.org/zh-cn/%E8%B4%9D%E5%B0%94%E6%9B%BC-%E7%A6%8F%E7%89%B9%E7%AE%97%E6%B3%95#.E6.9D.BE.E5.BC.9B
版权声明:本文为博主原创文章,未经博主允许不得转载。
Bellman-Ford算法及其队列优化(SPFA)的更多相关文章
- Bellman—Ford算法思想
---恢复内容开始--- Bellman—Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题.对于给定的带权(有向或无向)图G=(V,E),其源点为s,加权函数w是边集E的映射.对图G ...
- Bellman - Ford 算法解决最短路径问题
Bellman - Ford 算法: 一:基本算法 对于单源最短路径问题,上一篇文章中介绍了 Dijkstra 算法,但是由于 Dijkstra 算法局限于解决非负权的最短路径问题,对于带负权的图就力 ...
- 基于bellman-ford算法使用队列优化的spfa求最短路O(m),最坏O(n*m)
acwing851-spfa求最短路 #include<iostream> #include<cstring> #include<algorithm> #inclu ...
- Dijkstra算法与Bellman - Ford算法示例(源自网上大牛的博客)【图论】
题意:题目大意:有N个点,给出从a点到b点的距离,当然a和b是互相可以抵达的,问从1到n的最短距离 poj2387 Description Bessie is out in the field and ...
- 最短路径之Bellman-Ford算法的队列优化及邻接表
参考链接:https://blog.csdn.net/qq_40626497/article/details/81139344
- poj1860 bellman—ford队列优化 Currency Exchange
Currency Exchange Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 22123 Accepted: 799 ...
- 关于SPFA的双端队列优化
7.11 Update 我做题的时候发现这样写会RE 因为在使用双端队列优化SPFA的时候 在将一个点加入队列的时候,如果队列已经空了 那么一旦出现dis[Q.front()]就会RE 可以这样修改 ...
- SPFA(Bellman-Ford队列优化)
原理:队列+松弛操作 将源点加入队尾,每一步读取队头顶点u,并将队头顶点u出队(记得消除标记):将与点u相连的所有点v进行松弛操作,如果能更新距离(即令d[v]变小),那么就更新,另外,如果点v没有在 ...
- uva 558 - Wormholes(Bellman Ford判断负环)
题目链接:558 - Wormholes 题目大意:给出n和m,表示有n个点,然后给出m条边,然后判断给出的有向图中是否存在负环. 解题思路:利用Bellman Ford算法,若进行第n次松弛时,还能 ...
随机推荐
- 怎样查看电脑登录过的wifi密码?
https://jingyan.baidu.com/album/fcb5aff770f7e6edaa4a71d9.html?picindex=7
- java.time.ZonedDateTime
Java的日期与时间 ZonedDateTime类是Java 8中日期时间功能里,用于表示带时区的日期与时间信息的类.可以用于表示一个真实事件的开始时间,如某火箭升空时间等等. ZonedDateTi ...
- Django 动态导入配置文件的类
导入配置文件的类 #如何用字符串的形式动态导入模块 from importlib import import_module path=''api.cors.CORSMiddleware' #CORSM ...
- The given 'driver' ] is unknown, Doctrine currently supports only the follo wing drivers: pdo_mysql, pdo_sqlite, pdo_pgsql, pdo_oci, oci8, ibm_db2, pdo
[Doctrine\DBAL\DBALException] The given 'driver' ] ...
- 安装了包,pycharm却提示找不到包
这段时间,我爬虫爬到了一个论坛的数据,有个分析需要知道他的字符编码,因此使用到了 chardet,我在终端很顺利的安装了这个,但是在pycharm里使用的时候老是提示有错误,向下面这样: 其实这个是因 ...
- SM30 表格维护生成器
1)SE11创建自建表,结构如下: 2) 创建表维护 3) 针对上面创建的函数组ZMM_MAT_DESC,做以下增强处理 添加的Module 代码如下: module mod_customize in ...
- Python socket TCPServer Demo
#coding:utf-8 from SocketServer import TCPServer,BaseRequestHandler import traceback class MyBaseReq ...
- LRC歌词文件读取代码
/**************************************************/ /*******************-main文件-******************* ...
- mysql sql语句:行转列问题
存在表score,记录学生的考试成绩,如下图所示: 现要求以 学生姓名,语文,数学,英语 这种格式显示学生成绩,如下图所示 具体步骤如下: 1.首先,使用case when函数输出单个课程的成绩 ca ...
- Python 3 接口与归一化设计
一.接口与归一化设计: 1.归一化让使用者无需关心对象的类是什么,只需要知道这些对象都具备某些功能就可以了,这极大地降低了使用者的使用难度. 2.归一化使得高层的外部使用者可以不加区分的处理所有接口兼 ...