【bzoj1001】【最短路】【对偶图】【最大流转最小割】狼抓兔子题解

【BZOJ1001】狼抓兔子

1001: [BeiJing2006]狼抓兔子

Time Limit: 15 Sec  Memory Limit: 162 MB
Submit: 18872  Solved: 4647
[Submit][Status][Discuss]

Description

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，

而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路 

1:(x,y)<==>(x+1,y) 

2:(x,y)<==>(x,y+1) 

3:(x,y)<==>(x+1,y+1) 

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，

开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击

这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，

才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的

狼的数量要最小。因为狼还要去找喜羊羊麻烦.

Input

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值. 

第二部分共N-1行，每行M个数，表示纵向道路的权值. 

第三部分共N-1行，每行M-1个数，表示斜向道路的权值. 

输入文件保证不超过10M

Output

输出一个整数，表示参与伏击的狼的最小数量.

Sample Input

3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6

 

 

题目大意：如和将一张无向图割成完全不相连的两部分，并使被割的边总权值最小。

题解：刚看这道题的时候满脑子暴力，直到某大佬让我去学学对偶图然后给我说这是最短路问题后，才渐渐开始有了思路。在进入正题前我们得先了解对偶图是啥。

　　维基百科对对偶图（Dual Graph）的解释如下：

　　“In the mathematical discipline of graph theory, the dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge whenever two faces of G are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs (graphs that are already embedded in the plane) rather than planar graphs (graphs that may be embedded but for which the embedding is not yet known).”

　　根据维基百科的解释，对偶图中的每一个点即为平面图中的某一个面，对偶图中任意两点间的线都是平面图中对应两平面公共边的割线，如果平面图中某一条边只属于一个面，那么在对偶图中就是一个环边，注意平面图周围无边界的面也是对偶图中的一个点。

　　首先这是一个普通的平面图：

　　此平面图对应的对偶图即为：

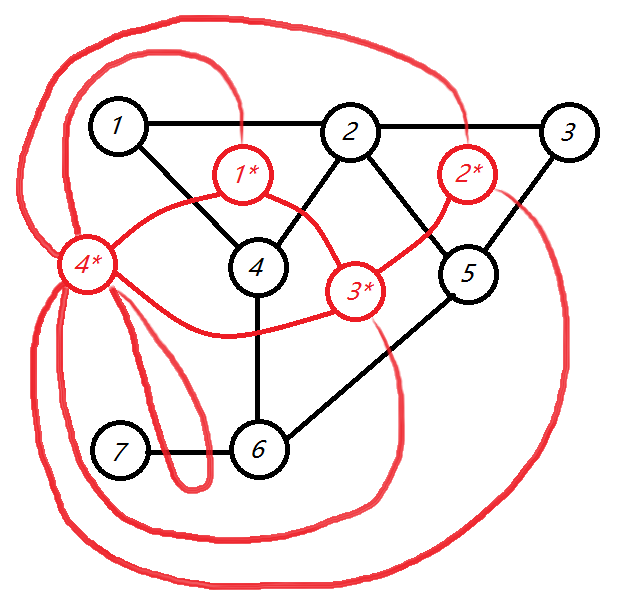
　　如图所示，对偶图的边数等于平面图的边数，对偶图的点数等于平面图的面数。

　　那么对偶图和这道题又有什么关系呢？

　　首先我们把起点和终点不与其他边交叉地连接起来构成一个新面，然后做出这个新平面图的对偶图，把对偶图中新面的点和无边界面的点之间的连线删去，求新面的点到无边界面的点的最短路即可（注意割线的权值即为被割边的权值）。这样求得的最短路就是原平面图的最小割。如下图所示（图源自网络）：

　　这样我们就可以将最大流问题转化为一个最小割问题，也就可以当成是最短路问题了。所以到这里这道题唯一的难点就在输入时处理平面图和对偶图并加边上了，用数学推导推导就好了，这里不再赘述。

　　下面贴AC代码：

 #include <cstdio>
 int N,M,cnt,end_pos,minn=1e9,star,ass,t;
 int pre[],dist[],quq[];//bzoj数据有毒，随意开上几百万别MLE了就行
 bool vis[];//最好别用int存，有可能超内存或者开内存的时候超时什么的
 struct pack {int to,next,len;} E[];
 void add_edge(int x,int y,int v){
     E[++cnt].to=x;E[cnt].next=pre[y];E[cnt].len=v;pre[y]=cnt;
     E[++cnt].to=y;E[cnt].next=pre[x];E[cnt].len=v;pre[x]=cnt;
 }
 int spfa(){
      while (star<=ass)
     {
         int x=quq[star];
         vis[quq[star++]]=false;
         for (int i=pre[x];i!=;i=E[i].next)
         {
             int y=E[i].to;
             if (dist[y]>dist[x]+E[i].len)
             {
                 dist[y]=dist[x]+E[i].len;
                 if (vis[y]==false)
                 {
                     quq[++ass]=y;
                     vis[y]=true;
                 }
             }
         }
     }
 }
 void input_adt(){
     scanf("%d%d",&N,&M); end_pos=*(N-)*(M-)+;
     if(N==){
         for(int i=;i<M;++i){
             scanf("%d",&t);
             if(t<minn) minn=t;
         }
         return ;
     }
     else if(M==){
         for(int i=;i<N;++i){
             scanf("%d",&t);
             if(t<minn) minn=t;
         }
         return ;
     }

     for(int i=;i<=end_pos;++i) dist[i]=1e9;

     for(int i=;i<=*(N-)+;i+=)
         for(int j=;j<M;++j){
             scanf("%d",&t);
 /*            if(N==1){
                 if(t<minn) minn=t;
             }*/
             if(i==) add_edge(j,,t);
             else if(i==*(N-)+) add_edge(end_pos-(M-j),end_pos,t);
             else add_edge((i-)*(M-)+j,(i-)*(M-)+j,t);
         }
 //    if(minn!=1e9) return ;

     for(int i=;i<*(N-)+;i+=)
         for(int j=;j<=M;++j){
             scanf("%d",&t);
 /*            if(M==1){
                 if(t<minn) minn=t;
             }*/
             if(j==) add_edge(i*(M-)+,end_pos,t);
             else if(j==M) add_edge(i*(M-),,t);
             else add_edge(i*(M-)+j,(i-)*(M-)+j-,t);
         }
 //    if(minn!=1e9) return ;

     for(int i=;i<*(N-)+;i+=)
         for(int j=;j<M;++j){
             scanf("%d",&t);
             add_edge((i-)*(M-)+j,i*(M-)+j,t);
         }
 }
 int main(){
     input_adt();
     if(minn==1e9){
         spfa();
         printf("%d",dist[end_pos]);
     }
     else printf("%d",minn);
     return ;
 }