【BZOJ3309】DZY Loves Math 莫比乌斯反演+线性筛（好题）

【BZOJ3309】DZY Loves Math

Description

对于正整数n，定义f(n)为n所含质因子的最大幂指数。例如f(1960)=f(2^3 * 5^1 * 7^2)=3, f(10007)=1, f(1)=0。
给定正整数a,b，求sigma(sigma(f(gcd(i,j)))) (i=1..a, j=1..b)。

Input

第一行一个数T，表示询问数。
接下来T行，每行两个数a,b，表示一个询问。

Output

对于每一个询问，输出一行一个非负整数作为回答。

Sample Input

4
7558588 9653114
6514903 4451211
7425644 1189442
6335198 4957

Sample Output

35793453939901
14225956593420
4332838845846
15400094813

HINT

【数据规模】
T<=10000
1<=a,b<=10^7

题解：其实如果熟悉了这类题的套路，本题也不是特别难的~

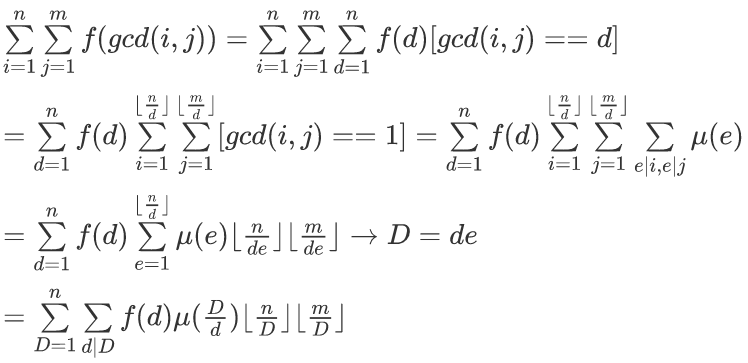
然后我们设$g(D)=\sum\limits_{d|D}f(d)\mu({D\over d})$，那么只要g能线性筛出来问题就解决了。

但是如何筛呢？我们还是先找个规律吧~

先从简单的开始，如果$D=p_1^{e_1}$，那么我们将和式展开，它等于：$f(p_1^{e_1})\times \mu(1)+f(p_1^{e_1-1})\times \mu(p_1)$，余下的项呢？剩下的都是mu=0啦！所以$g(D)=e_1-(e_1-1)=1$。

我们继续，如果$D=p_1^{e_1}*p_2^{e_2}$，那么$g(D)=max(e_1,e_2)-max(e_1-1,e_2)-max(e_1,e_2-1)+max(e_1-1,e_2-1)$，先假设${e_1=e_2}$，那么原式=$e_1-e_1-e_1+(e_1-1)=-1$；那如果$e_1<e_2$呢？原式=$e_2-e_2-(e_2-1)+(e_2-1)=0$。

接下来，如果$D=p_1^{e_1}*p_2^{e_2}$，还是先假设$e_1=e_2=e_3$，那么$g(D)=max(e_1,e_2,e_3)-max(e_1-1,e_2,e_3)-max(e_1,e_2-1,e_3)-max(e_1,e_2,e_3-1)+max(e_1-1,e_2-1,e_3)-max(e_1-1,e_2,e_3-1)-max(e_1,e_2-1,e_3-1)+max(e_1-1,e_2-1,e_3-1)=e_1-e_1-e_1-e_1+e_1+e_1+e_1-(e_1-1)=1$，唉？看出什么模式了吗？

如果$g(D)=\prod\limits_{i=1}^kp_i^{e_i}$，其中$e_1=e_2=...=e_k$，那么$g(D)=(-1)^{k+1}$，这个猜想是正确的吗？显然，因为在上面的式子中，只要max里有一个ei，那么整个max的值就是$e_1$，也就意味着除了最后一项的绝对值是$e_1-1$，其余所有项的绝对值都是$e_1$。并且，如果我们将原式看成：在k个物品中取出若干个，并用$e_i$表示取，用$e_i-1$表示不取，那么显然取出奇数个物品和取出偶数个物品的方案数是相同的，也就意味着在这些max的符号中，正号和负号的个数是相同的，所以我们只需要考虑最后一项$e_i-1$的符号就行了。显然，它的符号只取决于k的奇偶性。

好了，我们已经处理完$e_1=e_2=...=e_k$的情况了，现在处理它们不完全相等的情况。上面已经有例子证明当k=2时，g(D)=0了，那么是不是所有这样的g(D)都等于0呢？答案：是的。我们不妨设$e_1<e_2=e_3=...=e_k$，那么因为$e_1$比所有$e_i(i>2)$都小，所以$e_1$一定也不超过任何的$e_i-1(i>2)$。也就是说，如果在上面的max式中将$e_1$去掉，max式的值是不发生改变的。那么上面的max式的值都变成了什么呢？除了$max(e_1-1,e_2-1,e_3-1...e_k-1)$和$max(e_1-1,e_2,e_3...e_k)$的绝对值等于$e_2-1$以外，其余的max式的绝对值都是$e_2$。并且，因为形如$max(e_1,...)$和$max(e_1-1,...)$的式子的个数是相等的，它们的正负号也一定是一一对应的。既然绝对值都相等，符号都相对了，答案自然是等于0的。

然后就没啦！我们可以开始线性筛g数组啦！具体怎么筛呢？这里只提供大致方法：维护mn[i]表示i的最小质因子的次数，mx[i]表示i的出现次数最多的质因子的次数，xp[i]表示出现次数最多的质因子有多少个（如果有出现次数不相同的质因子，那么xp=0）。此时的线性筛已经不再是线性筛，而是一个DP...

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int maxn=10000010;
const int N=10000000;
typedef long long ll;
int pri[maxn/10],mx[maxn],mn[maxn],xp[maxn],f[maxn];
bool np[maxn];
int n,a,b,num;
ll ans;
inline int rd()
{
	int ret=0,f=1;	char gc=getchar();
	while(gc<'0'||gc>'9')	{if(gc=='-')f=-f;	gc=getchar();}
	while(gc>='0'&&gc<='9')	ret=ret*10+gc-'0',gc=getchar();
	return ret*f;
}
int main()
{
	int i,j,k;
	f[1]=0;
	for(i=2;i<=N;i++)
	{
		if(!np[i])	pri[++num]=i,mn[i]=1,f[i]=1;
		else
		{
			if(xp[i]==-1||(xp[i]&&mn[i]!=mx[i]))	f[i]=0;
			else	f[i]=(xp[i]&1)?-1:1;
		}
		f[i]+=f[i-1];
		for(j=1;j<=num&&i*pri[j]<=N;j++)
		{
			k=i*pri[j],np[k]=1;
			if(xp[i]==-1)	xp[k]=-1;
			else	if(i%pri[j]==0)
			{
				mn[k]=mn[i]+1,xp[k]=xp[i],mx[k]=mx[i];
				break;
			}
			else
			{
				if(!xp[i])	xp[k]=1,mx[k]=mn[i],mn[k]=1;
				else	if(mn[i]!=mx[i])	xp[k]=-1;
				else	xp[k]=xp[i]+1,mn[k]=1,mx[k]=mn[i];
			}
		}
	}
	int T=rd(),last,n,m;
	while(T--)
	{
		ans=0,n=rd(),m=rd();
		if(n>m)	swap(n,m);
		for(i=1;i<=n;i=last+1)
		{
			last=min(n/(n/i),m/(m/i));
			ans+=(ll)(f[last]-f[i-1])*(n/i)*(m/i);
		}
		printf("%lld\n",ans);
	}
	return 0;
}