Cayley凯莱定理——一一对应

定理

过$n$个有标志顶点的树的数目等于$n^{n-2}$。

此定理说明用$n-1$条边将$n$个已知的顶点连接起来的连通图的个数是$n^{n-1}$。也可以这样理解，将n个城市连接起来的树状网络有$n^{n-1}$种可能方案.所谓树状，指的是用$n-1$条边将$n$个城市连接起来，即无环。当然，建造一个树状网络一般是求其长度最短或造价最少等.Cayley定理只能说明可能方案的数目。

证明

Cayley定理的证明方法很多，下面采用最聪明也是最容易理解的一一对应法。不失一般性，假定已知的n个顶点标志为1,2,..n.

假设$T$是其中一棵树，树叶中有标号最小的，设为$a_1$，$a_1$的临界点为$b_1$，从图中消去$a_1$点和边$(a_1,b_1)$，$b_1$点便成为消去后余下的树$T_1$的顶点。在余下的树$T_1$中继续寻找标号最小的树叶，设为$a_2$，$a_2$的邻接点为$b_2$，从$T_1$中消去$a_2$及边$(a_2,b_2)$。如此步骤共执行n-2次，直到最后只剩下一条边为止.于是一棵树对应一序列

$$b_1,b_2,\cdots ,b_{n-2}$$

$b_1,b_2,\cdots ,b_{n-2}$是1到n的数，并且允许重复。

反过来从$b_1 b_2 \cdots b_{n-2}$可以恢复树$T$本身，方法如下：

一个是顶点标号的有序序列

$$1,2, \cdots ,n  \tag{1} $$

另一个是生成的序列

$$b_1,b_2,\cdots ,b_{n-2} \tag{2}$$

过程：在序列(1)中找出第一个不出现在序列(2)中的数，这个数显然便是$a_1$，同时形成的边$(a_1,b_1)$，并从(1)中消去$a_1$，从(2)中消去$b_1$，在余下的序列(1)、(2)中继续以上的步骤n-2次，直到序列(2)为空集为止。这时序列(1)剩下的两个数$a_k$，$b_k$，边$(a_k,b_k)$是树T的最后一条边。

以下图说明上述步骤：

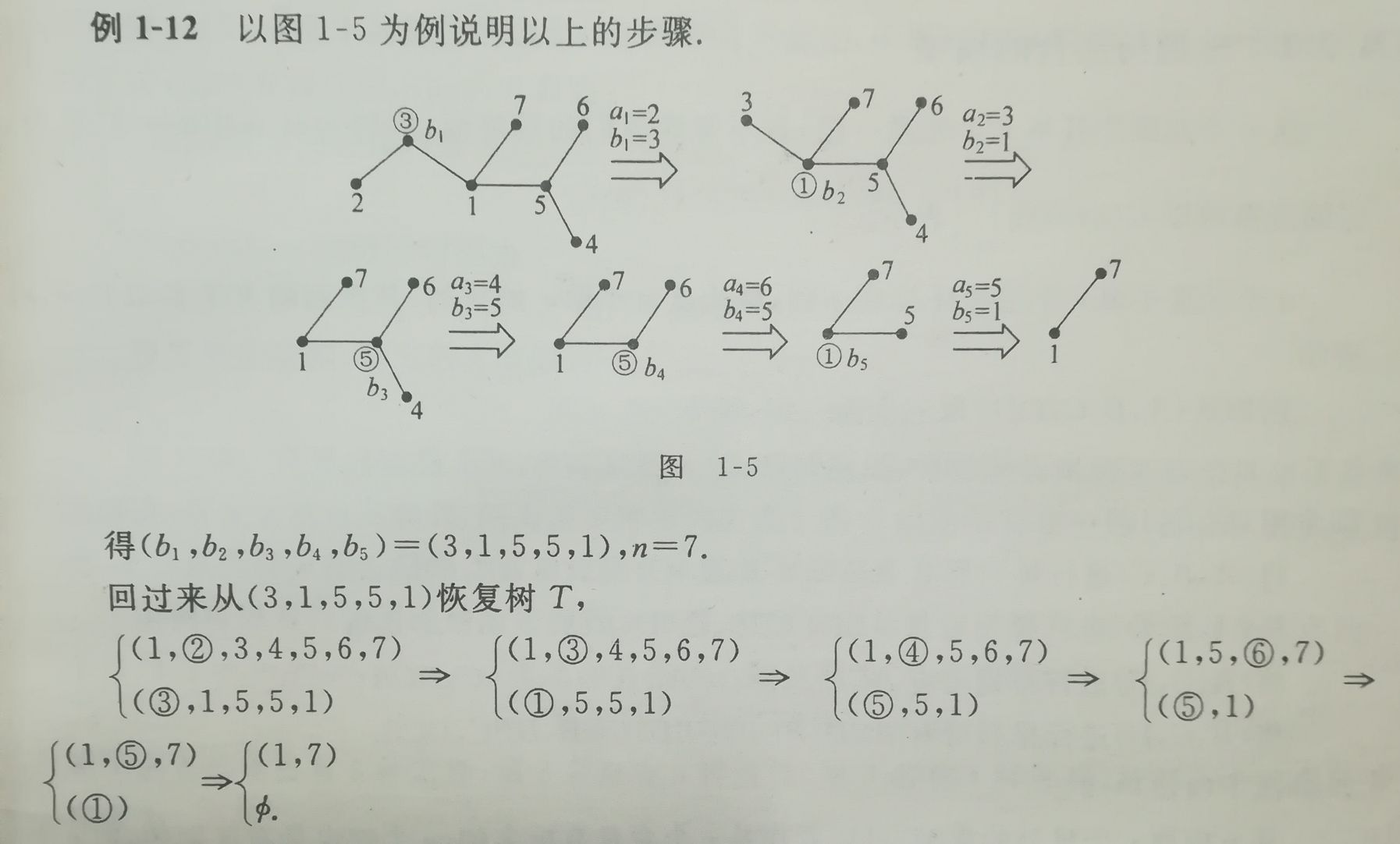
上面的过程说明过n个已知标号的顶点的树和序列$b_1b_2 \cdots b_{n-2}$一一对应，根据乘法法则可得，过n个有标号（相当于互异）的顶点的树的数目，由于$1\leq b_i\leq n,i=1,2,\cdots,n-2$，故为$n^{n-2}$个.

Cayley定理的证明过程实际上是提供了构造过n个有标号顶点的树的方法。

（参考书：组合数学   卢开澄、卢华明等编著）