【思维题 线段树】cf446C. DZY Loves Fibonacci Numbers

我这种maintain写法好zz。考试时获得了40pts的RE好成绩

In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation

F1 = 1; F2 = 1; Fn = Fn - 1 + Fn - 2 (n > 2).

DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of n integers: a1, a2, ..., an. Moreover, there are mqueries, each query has one of the two types:

1. Format of the query "1 l r". In reply to the query, you need to add Fi - l + 1 to each element ai, where l ≤ i ≤ r.
2. Format of the query "2 l r". In reply to the query you should output the value of 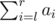 modulo 1000000009 (109 + 9).

Help DZY reply to all the queries.

Input

The first line of the input contains two integers n and m (1 ≤ n, m ≤ 300000). The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — initial array a.

Then, m lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1 ≤ l ≤ r ≤ n holds.

Output

For each query of the second type, print the value of the sum on a single line.

---

题目分析

注意到形如Fib的数列$a_{n+2}=a_{n+1}+a_n$有相当好的性质。

1. $a_n=F_{n−2}a_1+F_{n−1}a_2$
2. $\sum_{i=1}^na_i=a_{n+2}−a_2$

第一条可以用数学归纳法证明；第二条就是将$2\sum_{i=1}^na_i$展开，得到$\sum_{i=1}^na_i+a_{n+2}-a_2$.

回到这一道题上，利用了这两条性质，那么对于每一个修改的区间只需要保留区间前两项增加的Fib值就可以记录下这个操作。所以现在就可以用线段树来维护这一系列询问了。

 #include<bits/stdc++.h>
 #define MO 1000000009
 typedef long long ll;
 const int maxn = ;

 struct node
 {
     ll tag1,tag2,sum;
 }f[maxn<<];
 int n,m;
 ll sum[maxn],fib[maxn];

 int read()
 {
     char ch = getchar();
     int num = , fl = ;
     for (; !isdigit(ch); ch=getchar())
         if (ch=='-') fl = -;
     for (; isdigit(ch); ch=getchar())
         num = (num<<)+(num<<)+ch-;
     return num*fl;
 }
 void maintain(int rt, int lens)
 {
     f[rt].tag1 %= MO, f[rt].tag2 %= MO;
     f[rt].sum = f[rt<<].sum+f[rt<<|].sum;
     f[rt].sum = (f[rt].sum+f[rt].tag1*fib[lens]+f[rt].tag2*fib[lens+]-f[rt].tag2)%MO;
 }
 void pushdown(int rt, int l, int r)
 {
     if (!f[rt].tag1&&!f[rt].tag2) return;
     int mid = (l+r)>>, ls = rt<<, rs = rt<<|;
     f[ls].tag1 += f[rt].tag1, f[ls].tag2 += f[rt].tag2;
     f[rs].tag1 += f[rt].tag1*fib[mid-l]+f[rt].tag2*fib[mid-l+];
     f[rs].tag2 += f[rt].tag1*fib[mid-l+]+f[rt].tag2*fib[mid-l+];
     f[rt].tag1 = f[rt].tag2 = ;
     maintain(ls, mid-l+);
     maintain(rs, r-mid);
 }
 void modify(int rt, int L, int R, int l, int r)
 {
     if (L <= l&&r <= R){
         f[rt].tag1 += fib[l-L+];
         f[rt].tag2 += fib[l-L+];
         maintain(rt, r-l+);
         return;
     }
     int mid = (l+r)>>;
     pushdown(rt, l, r);
     if (L <= mid) modify(rt<<, L, R, l, mid);
     if (R > mid) modify(rt<<|, L, R, mid+, r);
     maintain(rt, r-l+);
 }
 ll query(int rt, int L, int R, int l, int r)
 {
     if (L <= l&&r <= R) return f[rt].sum;
     pushdown(rt, l, r);
     int mid = (l+r)>>;
     ll ret = ;
     if (L <= mid) ret += query(rt<<, L, R, l, mid);
     if (R > mid) ret += query(rt<<|, L, R, mid+, r);
     return ret%MO;
 }
 int main()
 {
     n = read(), m = read(), fib[] = fib[] = ;
     for (int i=; i<=n; i++) sum[i] = (sum[i-]+read())%MO;
     for (int i=; i<=; i++) fib[i] = (fib[i-]+fib[i-])%MO;
     for (int i=; i<=m; i++)
     {
         int opt = read(), l = read(), r = read();
         if (opt==) modify(, l, r, , n);
         else printf("%lld\n",(query(, l, r, , n)+(sum[r]-sum[l-])%MO+MO)%MO);
     }
     return ;
 }

END