【算法day3】小和、荷兰国旗、快排

小和问题

现有数组[1,3,4,2,5]

1左边是0（小于1），所以1的小和为0

3左边是1（小于3），所以3的小和为1

4左边是1、3（均小于4），所以4的小和为1+3=4

2左边是1、3、4（只有1小于2），所以2的小和为1

5左边是1、3、4、2（均小于5），所以5的小和为1+3+4+2=10

数组的小和为0+1+4+1+10=16

上述方法是从“左边有几个数比当前数小”的角度去解决

还可以转化为“右边有几个数比当前数大”来解

现有数组[1,3,4,2,5]

1右边有4个数大于1，有4个小和（4）；

3右边有2个数大于3，有2个小和（6）；

4右边有1个数大于4，有1个小和（4）；

2右边有1个数大于2，有1个小和（2）；

5右边没有（0）

4+6+4+2+0=16

荷兰国旗问题

问题一

给定一个数组arr，和一个数num，请把小于等于num的数放在数组的左边，大于num的数放在数组的右边。要求额外空间复杂度0(1)，时间复杂度O(N)

思路：

准备一个变量表示小于等于num的右边界【num定为5算了】

≤)[3,5,6,7,4,3,5,8]
  ↑
  i

此时有两种逻辑：

1、 当前数[i]≤num，则把当前的数[i]和小于等于区域"≤)"中的下一个数交换，然后"≤)"向右扩，i++；

2、当前数[i]＞num，直接跳下一个数，i++；

≤)[3,5,6,7,4,3,5,8]
   ↑
   i

当指针来到3时，3≤5，区域"≤)"向右扩，i++

≤[3),5,6,7,4,3,5,8]
     ↑
     i
≤[3,5),6,7,4,3,5,8]
       ↑
       i

到5时同理

到6时满足第二种条件，直接跳下一个数，i++

≤[3,5),6,7,4,3,5,8]
         ↑
         i
≤[3,5),6,7,4,3,5,8]
           ↑
           i

到7时同理，直接跳下一个数，i++

到4时满足条件1，把4与"≤)"区域的下一个数交换，4与6交换，区域"≤)"向右扩，i++

≤[3,5),4,7,6,3,5,8]
           ↑
           i
≤[3,5,4),7,6,3,5,8]
           ↑
           i
≤[3,5,4),7,6,3,5,8]
             ↑
             i

以此类推，当区域"≤)"扩到整个数组范围时结束

问题二(荷兰国旗问题)

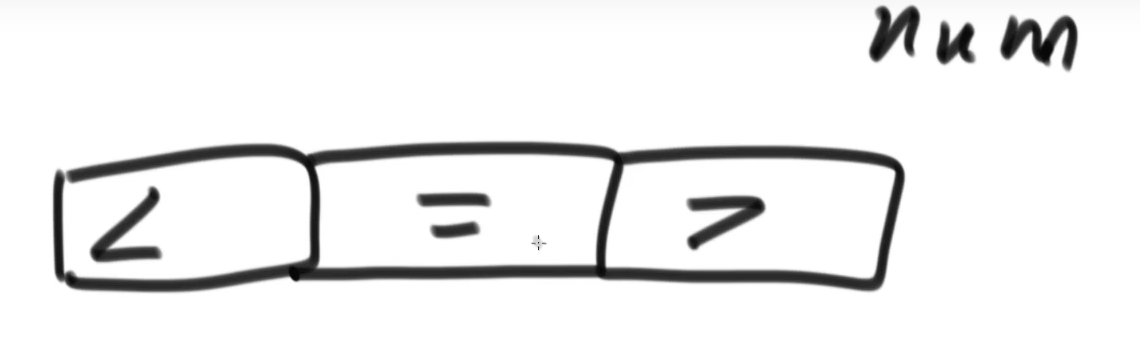
给定一个数组arr，和一个数num，请把小于num的数放在数组的左边，等于num的数放在数组的中间，大于num的数放在数组的右边。要求额外空间复杂度0(1)，时间复杂度0(N)

思路：

还是跟前一个问题类似，准备两个变量，一个表示小于5的右边界，另一个表示大于5的左边界

＜)[3,5,6,3,4,5,2,6,9,0](＞
  ↑
  i

此时每来到一个置就会有3种情况

1、当前数[i]＜num，则把当前的数[i]和小于区域"＜)"中的下一个数交换，然后"＜)"向右扩，i++；

2、当前数[i]=num，，直接跳下一个数，i++；

3、当前数[i]＞num，则把当前的数[i]和大于区域"＞)"中的前一个数交换，然后"＞)"向左扩，i++；

当指针来到3时，3＜5，区域"＜)"向右扩，i++

＜[3),5,6,3,4,5,2,6,9,0](＞
   ↑
   i
＜[3),5,6,3,4,5,2,6,9,0](＞
      ↑
      i

当指针来到5时，等于5，直接跳下一个

＜[3),5,6,3,4,5,2,6,9,0](＞
        ↑
        i
＜[3),5,0,3,4,5,2,6,9,6](＞
        ↑
        i
＜[3),5,0,3,4,5,2,6,9,(6]＞
        ↑
        i

当指针来到6时，6＞5，6和大于区域"＞)"中的前一个数交换，6和0交换，i原地不动（因为还没检查过它）

此时，检查新交换到i位置的数，发现其＜5，则0和小于区域"＜)"中的下一个数交换，然后"＜)"向右扩，i++；

＜[3),5,0,3,4,5,2,6,9,(6]＞
        ↑
        i
＜[3),0,5,3,4,5,2,6,9,(6]＞
        ↑
        i
＜[3,0),5,3,4,5,2,6,9,(6]＞
          ↑
          i

以此类推，当i遇到大于区域的边界时停止

最后两边就剩下大于小于的区域，而中间是等于的

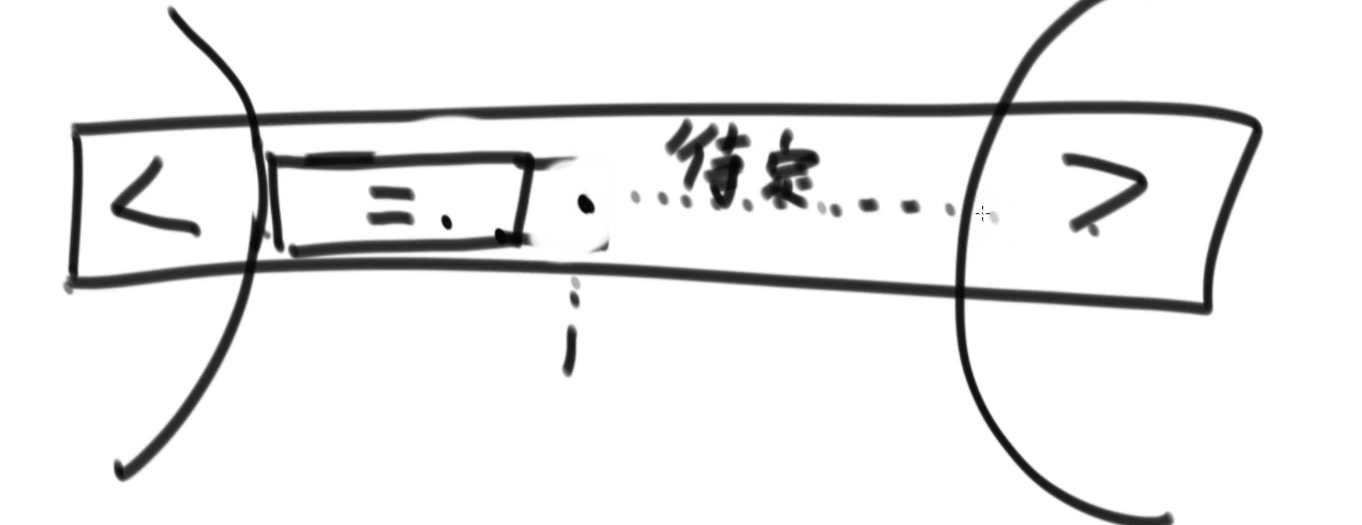
结束

快排

1.0版

例如

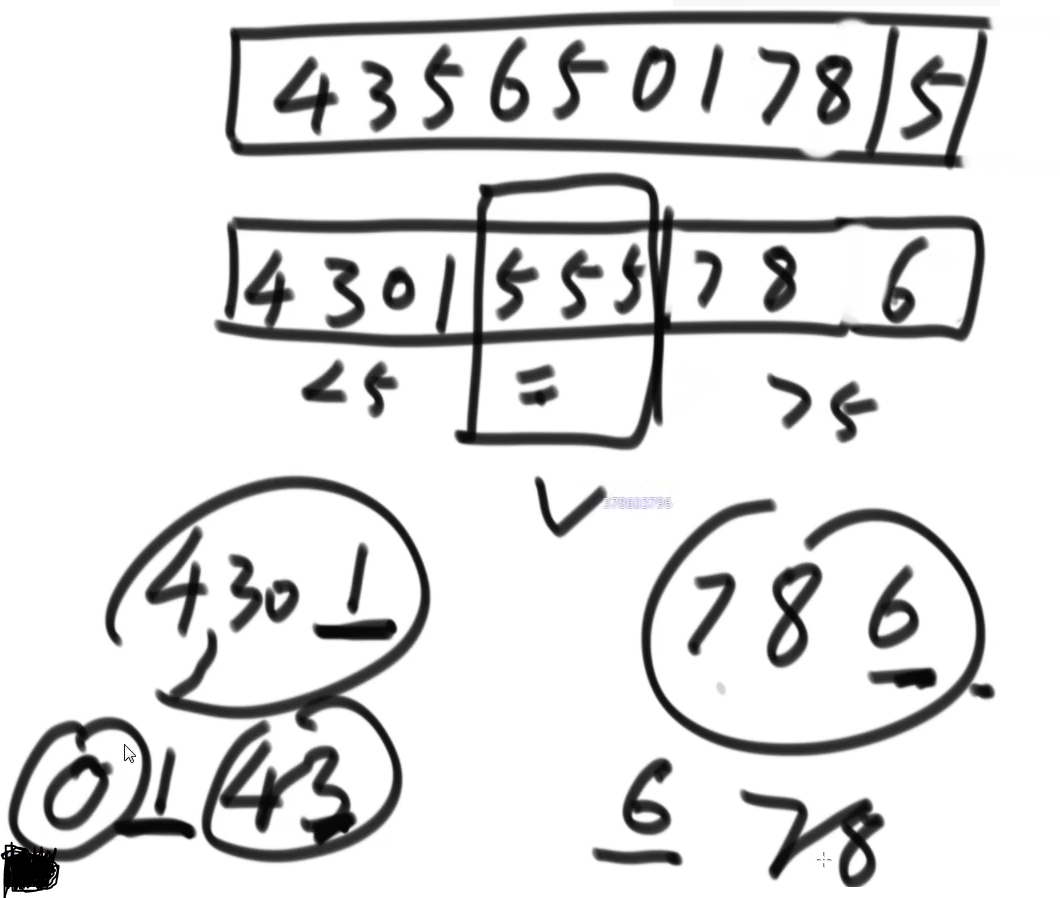
现在有一个数组，拿数组的最后一个数作为划分值

然后让它前面的一段做到左边的为≤num，右边的为＞num，设num为5吧

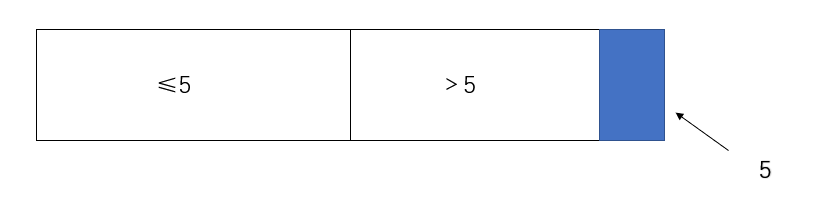
然后5和大于区域的第一个数做交换

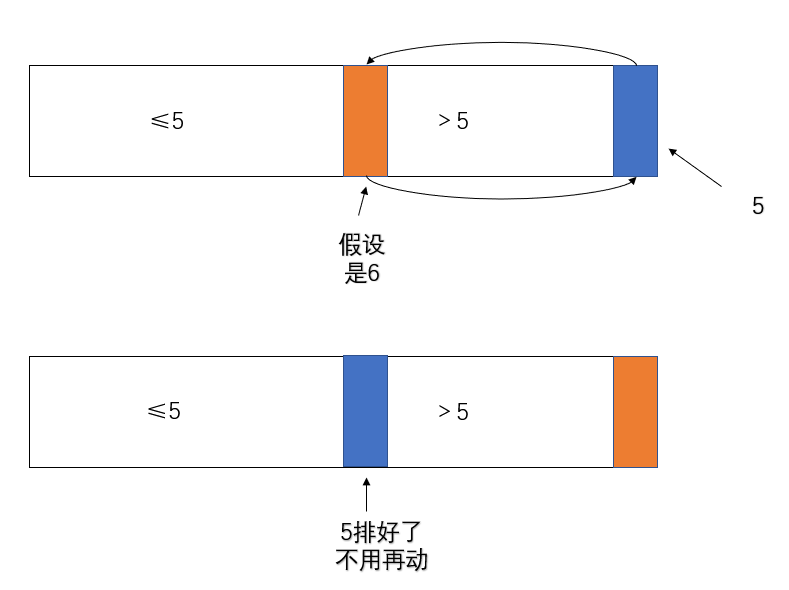
然后再把圈上的区域再重复进行之前的操作（拿最后一个数作为划分值）

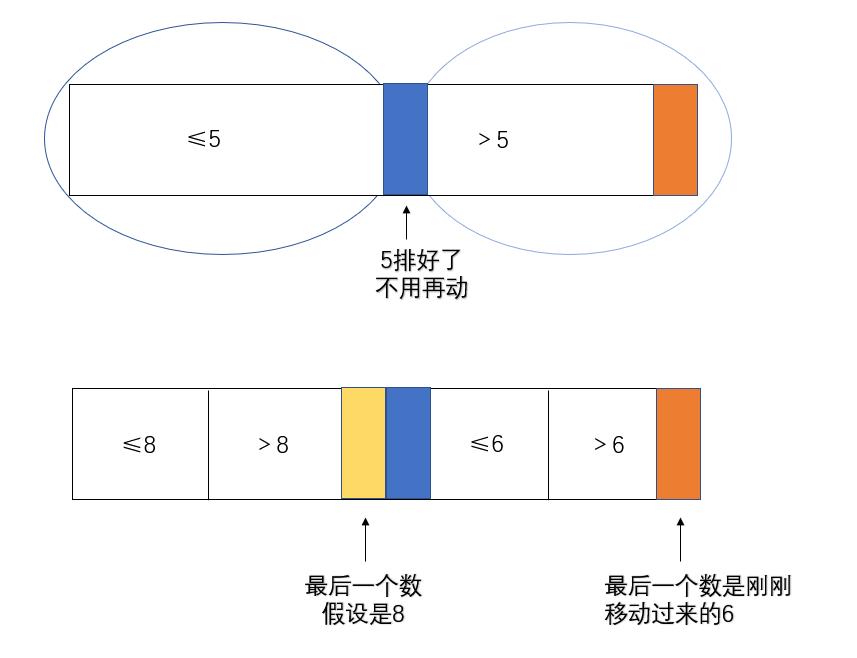
例如：

因为每次只保证一个数排好，所以递归到最后一定是有序的

2.0版

是以荷兰国旗问题为基础，也是最开始选数组的最后一个数作为划分值，不同的是，每次排完数组中间都是等于划分值的数，相当于每次搞定一批数的排序。

然后再在小于和大于区域重复上述操作直到排序结束

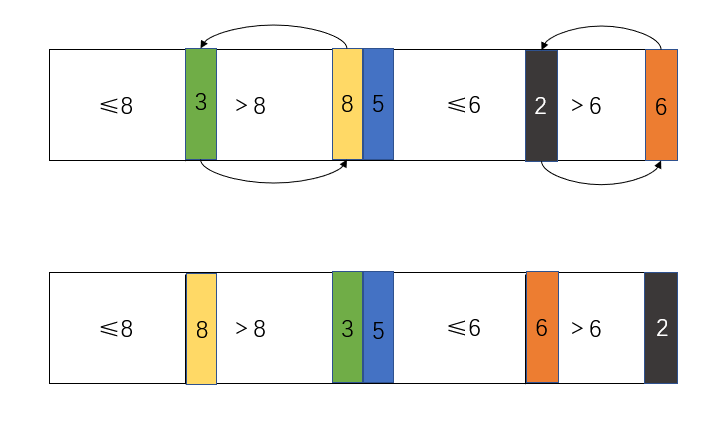
以5为例子

2.0和1.0在一些人为构建的数据中有可能会存在复杂度降低（好情况）或变高（坏情况）的情况

3.0版

在数组中随机选一个数作为划分值，将该数与数组最后一个数做交换再划分

由此，划分时出现好情况和坏情况就变成了概率事件，而且是等概率事件，因此该算法通过数学计算后的显示复杂度为O(Nlog₂N)