集成学习的不二法门bagging、boosting和三大法宝<结合策略>平均法，投票法和学习法（stacking）

单个学习器要么容易欠拟合要么容易过拟合，为了获得泛化性能优良的学习器，可以训练多个个体学习器，通过一定的结合策略，最终形成一个强学习器。这种集成多个个体学习器的方法称为集成学习(ensemble learning)。

集成学习通过组合多种模型来改善机器学习的结果，与单一的模型相比，这种方法允许产生更好的预测性能。

集成学习属于元算法，即结合数个“好而不同”的机器学习技术，形成一个预测模型，以此来降方差（bagging），减偏差（boosting），提升预测准确性（stacking）。

1. 集成学习之个体学习器

个体学习器（又称为“基学习器”）的选择有两种方式：

• 集成中只包含同种类型的个体学习器，称为同质集成 。
• 集成中包含不同类型的个体学习器，为异质集成 。

目前同质集成 的应用最广泛，而基学习器使用最多的模型是CART决策树和神经网络。

按照个体学习器之间是否存在依赖关系可以分为两类：

• 个体学习器之间存在强依赖关系，一系列个体学习器基本必须串行生成，代表是boosting系列算法。
• 个体学习器之间不存在强依赖关系 ，一系列个体学习器可以并行生成，代表是bagging系列算法。

1.1 boosting算法原理

boosting的算法原理如下所示：

Boosting算法的工作机制是：

（1）先从初始训练集训练出一个基学习器；

（2）再根据基学习器的表现对样本权重进行调整，增加基学习器误分类样本的权重（又称重采样）；

（3）基于调整后的样本分布来训练下一个基学习器；

（4）如此重复进行，直至基学习器数目达到事先指定的个数  ，将这  个基学习器通过集合策略进行整合，得到最终的强学习器。

Boosting系列算法里最著名算法主要有AdaBoost算法和提升树(boosting tree)系列算法。提升树系列算法里面应用最广泛的是梯度提升树(Gradient Boosting Tree)<GDBT>。

1.1.1以adaboost算法为例

“强学习”和“弱学习”的概念：一个分类，如果存在一个多项式算法能够学习他，并得到很高的正确率，那么这个算法称为强学习器，反之如果正确率只是稍大于随机猜测（50%），则称为弱学习器。

在实际情况中，我们往往会发现弱学习器比强学习器更容易获得，所以就有了能否把弱学习器提升（boosting）为强学习器的疑问。

于是提升类方法应运而生，它代表了一类从弱学习器出发，反复训练，得到一系列弱学习器，然后组合这些弱学习器，构成一个强学习器的算法。

大多数boost方法会改变数据的概率分布（改变数据权值），具体而言就是提高前一轮训练中被错分类的数据的权值，降低正确分类数据的权值，使得被错误分类的数据在下轮的训练中更受关注；

然后根据不同分布调用弱学习算法得到一系列弱学习器实现的，再将这些学习器线性组合，具体组合方法是误差率小的学习器会被增大权值，误差率大的学习器会被减小权值，典型代表adaboost算法。

1.2. 集成学习之Bagging 算法原理

Bagging的算法原理如下：

bagging算法的工作机制为：

（1）对训练集利用自助采样法进行次随机采样，每次采样得到  个样本的采样集；

（2）对于这  个采样集，我们可以分别独立的训练出  个基学习器；

（3）再对这  个基学习器通过集合策略来得到最终的强学习器。

值得注意的是这里的随机采样采用的是自助采样法（Bootstrap sampling），自助采样法是一种有放回的采样。

即对于  个样本的原始训练集，我们每次先随机采集一个样本放入采样集，接着把该样本放回，这样采集  次，最终可以得到  个样本的采样集，由于是随机采样，这样每次的采样集是和原始训练集不同的，和其他采样集也是不同的。

对于一个样本，它每次被采集到的概率是  。不被采集到的概率为  。如果次采样都没有被采集中的概率是  。则  ，

即当抽样的样本量足够大时，在bagging的每轮随机采样中，训练集中大约有36.8%的数据没有被采集中。对于这部分大约36.8%的没有被采样到的数据，

我们常常称之为袋外数据（Out Of Bag, 简称OOB）。这些数据未参与训练集模型的拟合，可以用来检测模型的泛化能力。

bagging对于弱学习器最常用的一般也是决策树和神经网络。bagging的集合策略也比较简单，对于分类问题，通常使用相对多数投票法。对于回归问题，通常使用算术平均法。

2. 集成学习之结合策略

上面几节主要关注于学习器，下面就对集成学习之结合策略做一个总结。我们假定我得到的T个弱学习器是 

2.1 平均法

平均法通常用于回归问题。

最简单的平均是算术平均，即：
 
也可以是每个个体学习器的加权平均，即 ：
 
其中  是个体学习器  的权重，  。

2.2 投票法

对于分类问题通常使用投票法。

假设我们的预测类别是  ，对于任意一个预测样本  ，我们的  个弱学习器的预测结果分别是  。主要有以下三种：

• 相对多数投票法：也就是少数服从多数，即预测结果中票数最高的分类类别。如果不止一个类别获得最高票，则随机选择一个作为最终类别。
• 绝对多数投票法：即不光要求获得最高票，还要求票过半数。
• 加权投票法：每个弱学习器的分类票数要乘以一个权重，最终将各个类别的加权票数求和，最大的值对应的类别为最终类别。

2.3 Stacking

平均法和投票法仅是对弱学习器的结果做简单的逻辑处理，而stacking是再加上一层权重学习器（Meta Learner），基学习器（Base learner）的结果作为该权重学习器的输入，得到最终结果。

以两层为例，第一层由多个基学习器组成，其输入为原始训练集，第二层的模型则是以第一层基学习器的输出作为训练集进行再训练，从而得到完整的stacking模型。

如下图所示为Stacking的工作原理：

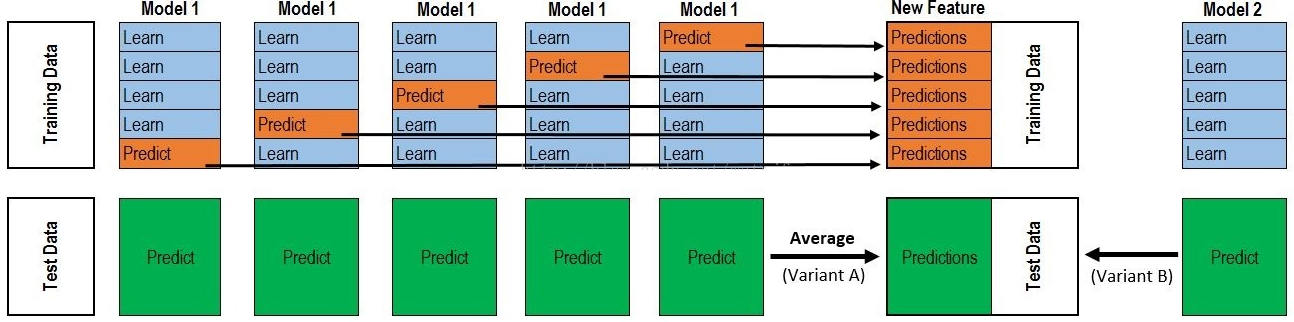
其中基学习器（Base learner）称为初级学习器，用于结合的学习器（Meta Learner）称为次级学习器。对于测试集，我们首先用初级学习器预测一次，将其输入次级学习器预测，得到最终的预测结果。

以5折划分为例，我们将原始训练集分为5折，分别记为fold1、fold2、fold3、fold4和fold5。此时我们使用fold2-fold5的数据来训练基模型1，并对fold1进行预测，该预测值即作为基模型1对fold1生成的元特征；

同样地，使用fold1、fold3-fold5的数据来训练基模型1，并对fold2进行预测，该预测值即作为基模型1对fold2生成的元特征；以此类推，得到基模型1对整个原始训练集生成的元特征。

同样地，对其他基模型也采用相同的方法生成元特征，从而构成用于第二层模型（下记为元模型，meta model）训练的完整元特征集。对于测试集，我们可以在每次基模型训练好时预测，再将预测值做均值处理；

也可以将基模型拟合全部的训练集之后再对测试集进行预测。

需要注意的是，在生成第二层特征的时候，各个基模型要采用相同的Kfold，这样得到的元特征的每一折（对应于之前的K折划分）都将不会泄露进该折数据的目标值信息 ，

从而尽可能的降低过拟合的风险。虽然如此，实际上我们得到的元特征还是存在一定程度上的信息泄露，比如我们在预测第二折的时候，是利用了第一折的目标值信息用于训练基模型的，

也就是说第一折的目标值信息杂糅在对第二折进行预测的基模型里。但是，实践中，这种程度的信息泄露所造成的过拟合程度很小。

可能还是比较抽象，那我们用案例描述一下：

上半部分是用一个基础模型进行5折交叉验证，如：用XGBoost作为基础模型Model1，5折交叉验证就是先拿出四折作为training data，另外一折作为testing data。

注意：在stacking中此部分数据会用到整个traing set。如：假设我们整个training set包含10000行数据，testing set包含2500行数据，那么每一次交叉验证其实就是对training set进行划分，在每一次的交叉验证中training data将会是8000行，testing data是2000行。

每一次的交叉验证包含两个过程，1. 基于training data训练模型；2. 基于training data训练生成的模型对testing data进行预测。

在整个第一次的交叉验证完成之后我们将会得到关于当前testing data的预测值，这将会是一个一维2000行的数据，记为a1。

注意！在这部分操作完成后，我们还要对数据集原来的整个testing set进行预测，这个过程会生成2500个预测值，

这部分预测值将会作为下一层模型testing data的一部分，记为b1。

因为我们进行的是5折交叉验证，所以以上提及的过程将会进行五次，最终会生成针对trainning set数据预测的5列2000行的数据a1,a2,a3,a4,a5，对testing set的预测会是5列2500行数据b1,b2,b3,b4,b5。

在完成对Model1的整个步骤之后，我们可以发现a1,a2,a3,a4,a5其实就是对原来整个training set的预测值，将他们拼凑起来，会形成一个10000行一列的矩阵，记为A1。

而对于b1,b2,b3,b4,b5这部分数据，我们将各部分相加取平均值，得到一个2500行一列的矩阵，记为B1。

以上就是stacking中一个模型的完整流程，stacking中同一层通常包含多个模型，假设还有Model2: LR，Model3：RF，Model4: GBDT，Model5：SVM，

对于这四个模型，我们可以重复以上的步骤，在整个流程结束之后，我们可以得到新的A2,A3,A4,A5,B2,B3,B4,B5矩阵。

在此之后，我们把A1,A2,A3,A4,A5并列合并得到一个10000行五列的矩阵作为training data，B1,B2,B3,B4,B5并列合并得到一个2500行五列的矩阵作为testing data。让下一层的模型，基于他们进一步训练。

其实西瓜书里讲的比较粗，我也不清楚到底是上面的博客讲错了，还是西瓜没有讲细节，吐血三升。

西瓜书内容如下：