[Scikit-learn] 2.5 Dimensionality reduction - Probabilistic PCA & Factor Analysis
2.5.4. Factor Analysis
PPCA的基本性质以及人肉推导：
以上假设z是标准正态分布的情况。以下是对z的分布的扩展，为general normal distribution。
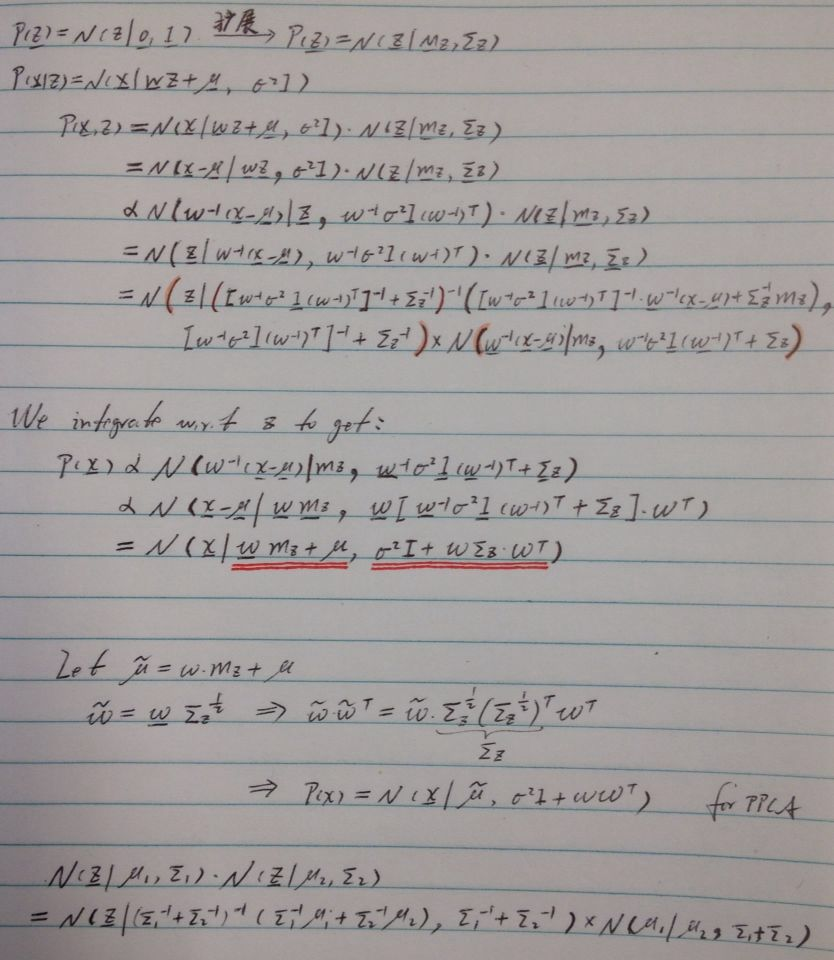
From: http://cs.brown.edu/courses/cs195-5/spring2012/lectures/2012-04-24_factorEM.pdf
PPCA可以选择input data，保持不变性；FA不能这么搞。
但它俩都可以选择latent variables。
From: https://www.cs.ubc.ca/~schmidtm/Courses/540-W16/L12.pdf
此处可见对x的分布的估计。
主成分分析和因子分析十大不同
一般情况下主成分用于探索性分析，很少单独使用，用主成分来分析数据，可以让我们对数据有一个大致的了解。
几个常用组合：
- 主成分分析+判别分析，适用于变量多而记录数不多的情况；
- 主成分分析+多元回归分析，主成分分析可以帮助判断是否存在共线性，并用于处理共线性问题；
- 主成分分析+聚类分析，不过这种组合因子分析可以更好的发挥优势。
因子分析：
- 首先，因子分析+多元回归分析，可以利用因子分析解决共线性问题；
- 其次，可以利用因子分析，寻找变量之间的潜在结构；
- 再次，因子分析+聚类分析，可以通过因子分析寻找聚类变量，从而简化聚类变量；
- 此外，因子分析还可以用于内在结构证实
Model selection with Probabilistic PCA and Factor Analysis (FA)
http://scikit-learn.org/stable/auto_examples/decomposition/plot_pca_vs_fa_model_selection.html
[Scikit-learn] 2.5 Dimensionality reduction - Probabilistic PCA & Factor Analysis的更多相关文章
- 机器学习课程-第8周-降维(Dimensionality Reduction)—主成分分析(PCA)
1. 动机一:数据压缩 第二种类型的 无监督学习问题,称为 降维.有几个不同的的原因使你可能想要做降维.一是数据压缩,数据压缩不仅允许我们压缩数据,因而使用较少的计算机内存或磁盘空间,但它也让我们加快 ...
- [UFLDL] Dimensionality Reduction
博客内容取材于:http://www.cnblogs.com/tornadomeet/archive/2012/06/24/2560261.html Deep learning:三十五(用NN实现数据 ...
- [Scikit-learn] 4.4 Dimensionality reduction - PCA
2.5. Decomposing signals in components (matrix factorization problems) 2.5.1. Principal component an ...
- Scikit Learn: 在python中机器学习
转自:http://my.oschina.net/u/175377/blog/84420#OSC_h2_23 Scikit Learn: 在python中机器学习 Warning 警告:有些没能理解的 ...
- Stanford机器学习笔记-10. 降维(Dimensionality Reduction)
10. Dimensionality Reduction Content 10. Dimensionality Reduction 10.1 Motivation 10.1.1 Motivation ...
- 可视化MNIST之降维探索Visualizing MNIST: An Exploration of Dimensionality Reduction
At some fundamental level, no one understands machine learning. It isn’t a matter of things being to ...
- 海量数据挖掘MMDS week4: 推荐系统之数据降维Dimensionality Reduction
http://blog.csdn.net/pipisorry/article/details/49231919 海量数据挖掘Mining Massive Datasets(MMDs) -Jure Le ...
- 第八章——降维（Dimensionality Reduction）
机器学习问题可能包含成百上千的特征.特征数量过多,不仅使得训练很耗时,而且难以找到解决方案.这一问题被称为维数灾难(curse of dimensionality).为简化问题,加速训练,就需要降维了 ...
- 壁虎书8 Dimensionality Reduction
many Machine Learning problems involve thousands or even millions of features for each training inst ...
随机推荐
- java_赋值与初始化
一.赋值(是给变量指定一个值或者是改变 一个变量的值) 变量类型 变量名=表达式 int i=10; 二.初始化 生成一个变量以后,必须通过明确的赋值语句进行初始化,然后在使用这个变量. 局部变量: ...
- opengl 4.5 中文api 链接
https://www.cnblogs.com/wiki3d/p/opengl_a.html
- Ubuntu系统---进行C++项目开发的工具
Ubuntu系统---进行C++项目开发的工具 在Ubuntu系统下进行C++工作任务,还没接触过.像 Windows + vs 一样,Ubuntu应该也有自己的C++开发工具.网上搜罗了一圈,发现有 ...
- Python3+Appium学习笔记09-元素定位android_uiautomator
appium是使用了uiautomator的框架的,所以uiautomator所带的定位方式.appium也是支持的 需要使用appium中find_element_by_android_uiauto ...
- bitset 来计算位
在stl中提供了 bitset<N> 来计算位,非常方便. 尤其是计算键盘的状态时游泳 ; bitset<> bs = s; cout<<bs[]<<e ...
- window open（） 方法
open() 方法用于打开一个新的浏览器窗口或查找一个已命名的窗口. 语法 window.open(URL,name,specs,replace) 参数 说明 URL 可选.打开指定的页面的URL.如 ...
- 使用selenium实现站长素材图片采集
from selenium import webdriver import requests,os from lxml import etree from selenium.webdriver.chr ...
- node.js的iconv模块----在linux上读取windows编码文件
有时候我们在windows上会保存一些中文文字信息文件,然而由于编码集的差异,这文件在linux上显示为乱码,其中一种解决方法是node.js的iconv模块 var fs = require('fs ...
- ACM-ICPC 2018 沈阳赛区现场赛 E. The Kouga Ninja Scrolls （切比雪夫距离+线段树）
题目链接: 题意:在二维平面上有 n 个人,每个人有一个位置(xi, yi)和门派 ci,m 个操作:①改变第 k 个人的位置:②改变第 k 个人的门派:③询问区间[l,r]之间不同门派的两个人的最大 ...
- How to connect oracle databse
1. 下載客戶端Oracle Developer Tools for Visual Studio_32bit 安裝后通過配置tnsnames.ora指定連接 C:\app\user name\prod ...