Java 平衡二叉树和AVL
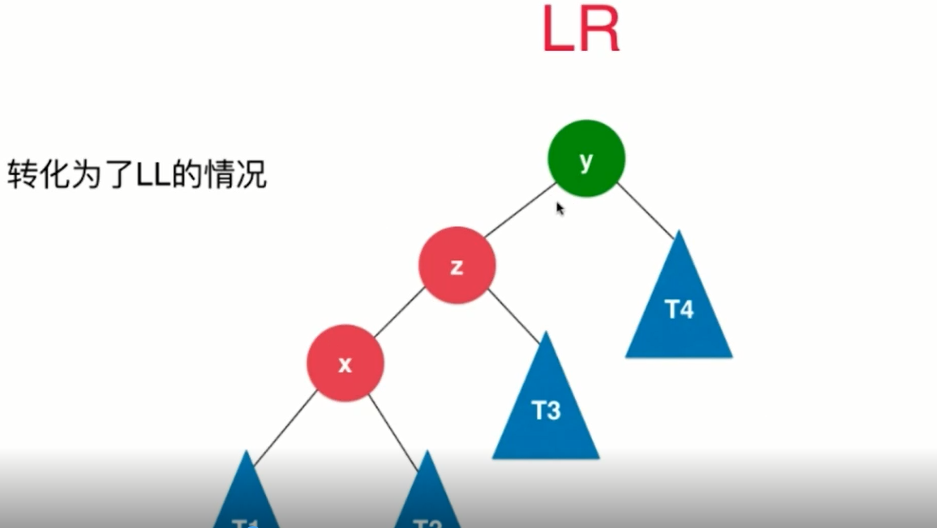
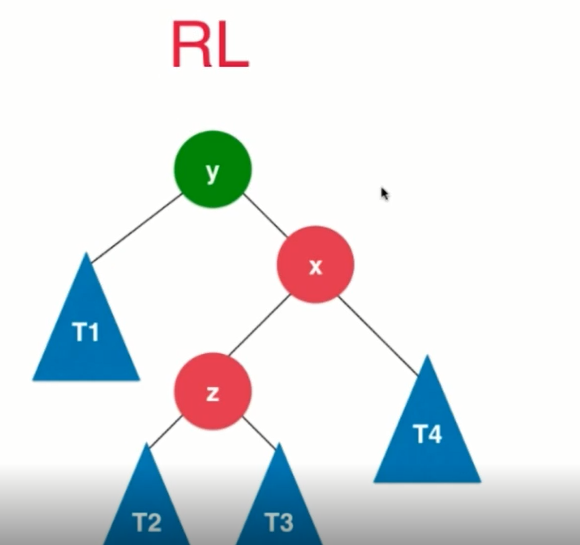
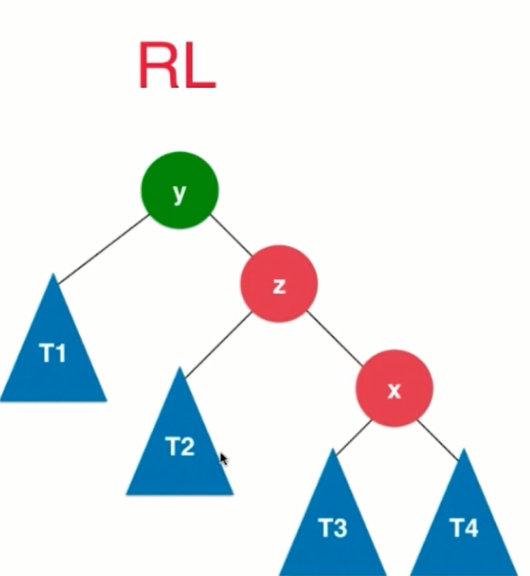
与BST<> 进行对比
import java.util.ArrayList;
import java.util.Collections; public class Main { public static void main(String[] args) { System.out.println("Pride and Prejudice"); ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size()); // Collections.sort(words); // Test BST
long startTime = System.nanoTime(); BST<String, Integer> bst = new BST<>();
for (String word : words) {
if (bst.contains(word))
bst.set(word, bst.get(word) + 1);
else
bst.add(word, 1);
} for(String word: words)
bst.contains(word); long endTime = System.nanoTime(); double time = (endTime - startTime) / 1000000000.0;
System.out.println("BST: " + time + " s"); // Test AVL Tree
startTime = System.nanoTime(); AVLTree<String, Integer> avl = new AVLTree<>();
for (String word : words) {
if (avl.contains(word))
avl.set(word, avl.get(word) + 1);
else
avl.add(word, 1);
} for(String word: words)
avl.contains(word); endTime = System.nanoTime(); time = (endTime - startTime) / 1000000000.0;
System.out.println("AVL: " + time + " s");
} System.out.println();
}
}
import java.util.ArrayList;
public class AVLTree<K extends Comparable<K>, V> {
private class Node{
public K key;
public V value;
public Node left, right;
public int height;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
height = 1;
}
}
private Node root;
private int size;
public AVLTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// 判断该二叉树是否是一棵二分搜索树
public boolean isBST(){
ArrayList<K> keys = new ArrayList<>();
inOrder(root, keys);
for(int i = 1 ; i < keys.size() ; i ++)
if(keys.get(i - 1).compareTo(keys.get(i)) > 0)
return false;
return true;
}
private void inOrder(Node node, ArrayList<K> keys){
if(node == null)
return;
inOrder(node.left, keys);
keys.add(node.key);
inOrder(node.right, keys);
}
// 判断该二叉树是否是一棵平衡二叉树
public boolean isBalanced(){
return isBalanced(root);
}
// 判断以Node为根的二叉树是否是一棵平衡二叉树，递归算法
private boolean isBalanced(Node node){
if(node == null)
return true;
int balanceFactor = getBalanceFactor(node);
if(Math.abs(balanceFactor) > 1)
return false;
return isBalanced(node.left) && isBalanced(node.right);
}
// 获得节点node的高度
private int getHeight(Node node){
if(node == null)
return 0;
return node.height;
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node){
if(node == null)
return 0;
return getHeight(node.left) - getHeight(node.right);
}
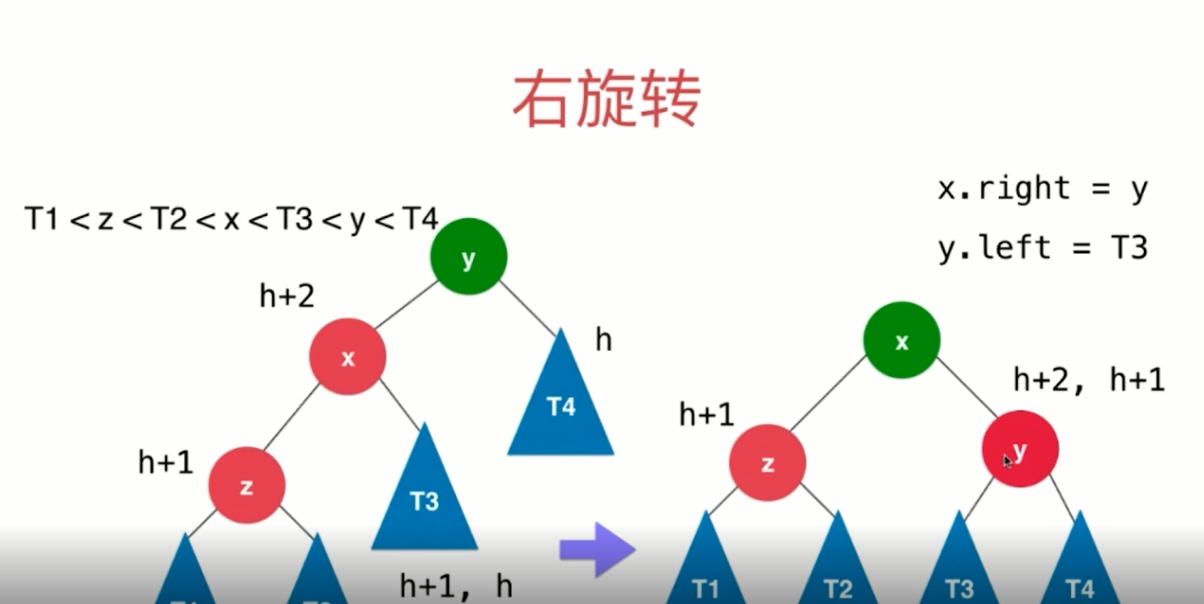
// 对节点y进行向右旋转操作，返回旋转后新的根节点x
// y x
// / \ / \
// x T4 向右旋转 (y) z y
// / \ - - - - - - - -> / \ / \
// z T3 T1 T2 T3 T4
// / \
// T1 T2
private Node rightRotate(Node y) {
Node x = y.left;
Node T3 = x.right;
// 向右旋转过程
x.right = y;
y.left = T3;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
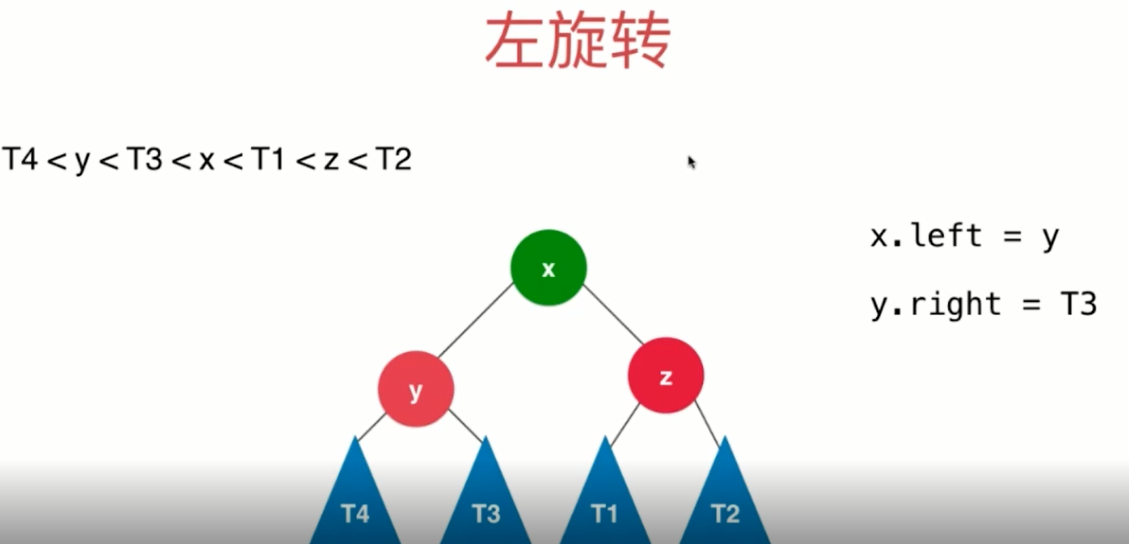
// 对节点y进行向左旋转操作，返回旋转后新的根节点x
// y x
// / \ / \
// T1 x 向左旋转 (y) y z
// / \ - - - - - - - -> / \ / \
// T2 z T1 T2 T3 T4
// / \
// T3 T4
private Node leftRotate(Node y) {
Node x = y.right;
Node T2 = x.left;
// 向左旋转过程
x.left = y;
y.right = T2;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
// 向二分搜索树中添加新的元素(key, value)
public void add(K key, V value){
root = add(root, key, value);
}
// 向以node为根的二分搜索树中插入元素(key, value)，递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
// 更新height
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
// 平衡维护
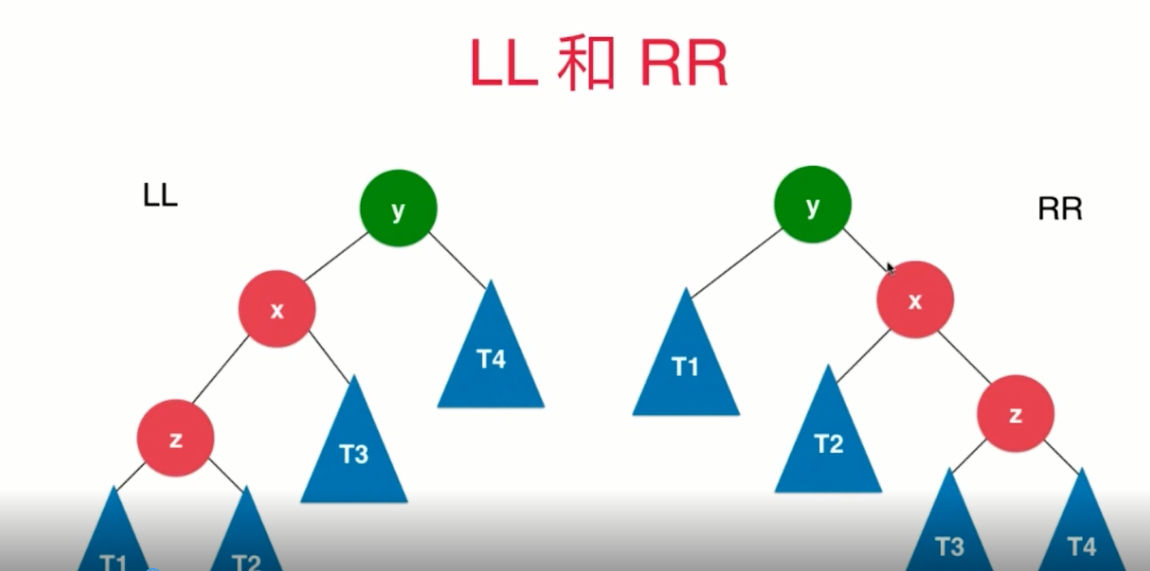
// LL
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
return rightRotate(node);
// RR
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0)
return leftRotate(node);
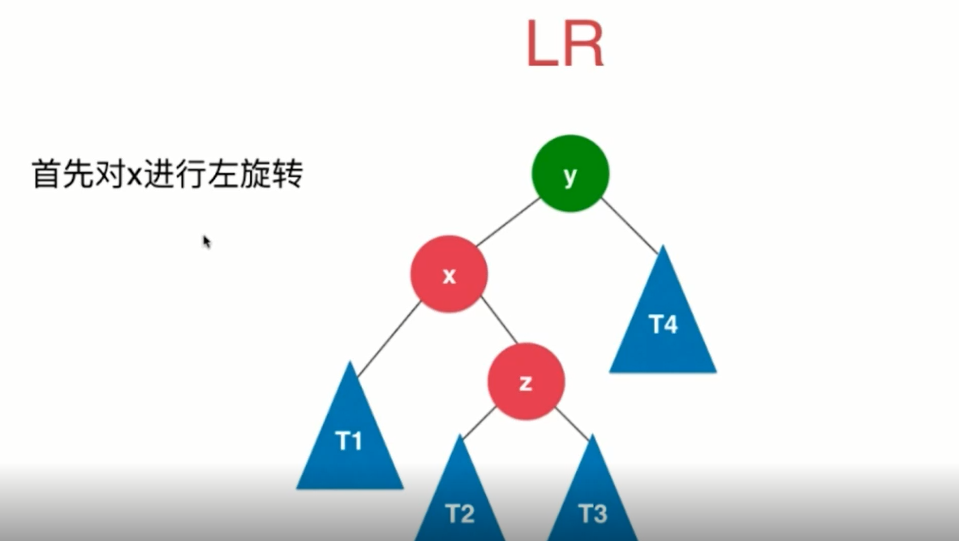
// LR
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// RL
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// 返回以node为根节点的二分搜索树中，key所在的节点
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// 从二分搜索树中删除键为key的节点
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
Node retNode;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
// return node;
retNode = node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
// return node;
retNode = node;
}
else{ // key.compareTo(node.key) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
// return rightNode;
retNode = rightNode;
}
// 待删除节点右子树为空的情况
else if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
// return leftNode;
retNode = leftNode;
}
// 待删除节点左右子树均不为空的情况
else{
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
//successor.right = removeMin(node.right);
successor.right = remove(node.right, successor.key);
successor.left = node.left;
node.left = node.right = null;
// return successor;
retNode = successor;
}
}
if(retNode == null)
return null;
// 更新height
retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
// 计算平衡因子
int balanceFactor = getBalanceFactor(retNode);
// 平衡维护
// LL
if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0)
return rightRotate(retNode);
// RR
if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0)
return leftRotate(retNode);
// LR
if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
retNode.left = leftRotate(retNode.left);
return rightRotate(retNode);
}
// RL
if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
return retNode;
}
}
public int[] intersect(int[] nums1, int[] nums2) {
AVLTree<Integer, Integer> map = new AVLTree<>();
for(int num: nums1){
if(!map.contains(num))
map.add(num, 1);
else
map.add(num, map.get(num) + 1);
}
ArrayList<Integer> res = new ArrayList<>();
for(int num: nums2){
if(map.contains(num)){
res.add(num);
map.add(num, map.get(num) - 1);
if(map.get(num) == 0)
map.remove(num);
}
}
int[] ret = new int[res.size()];
for(int i = 0 ; i < res.size() ; i ++)
ret[i] = res.get(i);
return ret;
}
public int uniqueMorseRepresentations(String[] words) {
String[] codes = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};
AVLTree<String, Object> set = new AVLTree<>();
for(String word: words){
StringBuilder res = new StringBuilder();
for(int i = 0 ; i < word.length() ; i ++)
res.append(codes[word.charAt(i) - 'a']);
set.add(res.toString(), null);
}
return set.getSize();
}
AvLMap：
public interface Map<K, V> {
void add(K key, V value);
boolean contains(K key);
V get(K key);
void set(K key, V newValue);
V remove(K key);
int getSize();
boolean isEmpty();
}
public class AVLMap<K extends Comparable<K>, V> implements Map<K, V> {
private AVLTree<K, V> avl;
public AVLMap(){
avl = new AVLTree<>();
}
@Override
public int getSize(){
return avl.getSize();
}
@Override
public boolean isEmpty(){
return avl.isEmpty();
}
@Override
public void add(K key, V value){
avl.add(key, value);
}
@Override
public boolean contains(K key){
return avl.contains(key);
}
@Override
public V get(K key){
return avl.get(key);
}
@Override
public void set(K key, V newValue){
avl.set(key, newValue);
}
@Override
public V remove(K key){
return avl.remove(key);
}
}
public interface Set<E> {
void add(E e);
boolean contains(E e);
void remove(E e);
int getSize();
boolean isEmpty();
}
public class AVLSet<E extends Comparable<E>> implements Set<E> {
private AVLTree<E, Object> avl;
public AVLSet(){
avl = new AVLTree<>();
}
@Override
public int getSize(){
return avl.getSize();
}
@Override
public boolean isEmpty(){
return avl.isEmpty();
}
@Override
public void add(E e){
avl.add(e, null);
}
@Override
public boolean contains(E e){
return avl.contains(e);
}
@Override
public void remove(E e){
avl.remove(e);
}
}
public int[] intersection(int[] nums1, int[] nums2) {
AVLSet<Integer> set = new AVLSet<>();
for(int num: nums1)
set.add(num);
ArrayList<Integer> list = new ArrayList<>();
for(int num: nums2){
if(set.contains(num)){
list.add(num);
set.remove(num);
}
}
int[] res = new int[list.size()];
for(int i = 0 ; i < list.size() ; i ++)
res[i] = list.get(i);
return res;
}
public int[] intersect(int[] nums1, int[] nums2) {
AVLMap<Integer, Integer> map = new AVLMap<>();
for(int num: nums1){
if(!map.contains(num))
map.add(num, 1);
else
map.add(num, map.get(num) + 1);
}
ArrayList<Integer> res = new ArrayList<>();
for(int num: nums2){
if(map.contains(num)){
res.add(num);
map.add(num, map.get(num) - 1);
if(map.get(num) == 0)
map.remove(num);
}
}
int[] ret = new int[res.size()];
for(int i = 0 ; i < res.size() ; i ++)
ret[i] = res.get(i);
return ret;
}
Java 平衡二叉树和AVL的更多相关文章
- 【Java】 大话数据结构(12) 查找算法(3) （平衡二叉树（AVL树））
本文根据<大话数据结构>一书及网络资料,实现了Java版的平衡二叉树(AVL树). 平衡二叉树介绍 在上篇博客中所实现的二叉排序树(二叉搜索树),其查找性能取决于二叉排序树的形状,当二叉排 ...
- Java数据结构（十四）—— 平衡二叉树（AVL树）
平衡二叉树(AVL树) 二叉排序树问题分析 左子树全部为空,从形式上看更像一个单链表 插入速度没有影响 查询速度明显降低 解决方案:平衡二叉树 基本介绍 平衡二叉树也叫二叉搜索树,保证查询效率较高 它 ...
- 树（三）——自平衡二叉树（AVL）
简介 自平衡二叉树(AVL)属于二叉平衡树的一类,此类树主要完成一个从键到值的查找过程,即字典(或映射),它维护树高度的方式与其他数据结构不同. 自平衡规则: AVL树的左.右子树都是AVL树 左.右 ...
- 【算法】论平衡二叉树（AVL）的正确种植方法
参考资料 <算法(java)> — — Robert Sedgewick, Kevin Wayne <数据结构> ...
- 数据结构之平衡二叉树（AVL）
一:平衡二叉树特点:平衡二叉树(Balanced binary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的,所以又称为AVL树 ...
- 详解什么是平衡二叉树（AVL）（修订补充版）
详解什么是平衡二叉树(AVL)(修订补充版) 前言 Wiki:在计算机科学中,AVL树是最早被发明的自平衡二叉查找树.在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树.查 ...
- 数据结构与算法——平衡二叉树（AVL树）
目录 二叉排序树存在的问题 基本介绍 单旋转(左旋转) 树高度计算 旋转 右旋转 双旋转 完整代码 二叉排序树存在的问题 一个数列 {1,2,3,4,5,6},创建一颗二叉排序树(BST) 创建完成的 ...
- 平衡二叉树（AVL）java实现
数的节点 package com.ydp.tree.AVLTree; public class Node{ private int data = 0; private Node lchild = nu ...
- java平衡二叉树AVL数
平衡二叉树(Balanced Binary Tree)具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树 右旋:在插入二叉树的时候,根节点的右侧高 ...
随机推荐
- 查看服务器内存、CPU、网络等占用情况的命令--汇总
搭建测试环境过程中,需要对正在使用的aws服务器(实际这是一台虚拟出来的服务器),查看它在运行脚本,启动脚本时的内存,CPU,网络等使用情况 1.查看服务器cpu内核个数: -cat 每个物理cpu中 ...
- hive 整合ranger
一.安装hive插件 1.解压安装 # tar zxvf ranger-2.0.0-SNAPSHOT-hive-plugin.tar.gz -C /data1/hadoop/ 2.修改install ...
- JS和JQuery实现Button绑定键盘Enter事件实现提交
JavaScript实现方法 document.onkeydown = function(e) { if (!e) e = window.event;//火狐中是 window.event if (( ...
- fluent meshing建立周期性网格
原视频下载地址:https://pan.baidu.com/s/1pKUXKgz 密码: 6pwh
- 最新版-Python和Java实现Aes相互加解密
前情 需要使用Python和Java实现同一个AES加解密算法,使Python版本加密的密文能够由Java代码解密,反之亦然. Python实现 Python为3.6版本 # -*- coding: ...
- 剑指offer：数组中只出现一次的数字
题目描述: 一个整型数组里除了两个数字之外,其他的数字都出现了两次.请写程序找出这两个只出现一次的数字. 思路分析: 1. 直接想法,每个数字遍历,统计出现次数,复杂度O(n^2),超时. 2. 借助 ...
- HTTP APIs 设计/规范指南
根据REST APIs的成熟度模型 ,此规范关注的是Level 2的APIs. 1 设计指南 HTTP APIs主要由四部分组成:HTTP,URL,资源,资源的表述(JSON).资源的表述格式通常都 ...
- CMU Database Systems - MVCC
MVCC是一种用空间来换取更高的并发度的技术 对同一个对象不去update,而且记录下每一次的不同版本的值 存在不会消失,新值并不能抹杀原先的存在 所以update操作并不是对世界的真实反映,这是一种 ...
- 关于jvm系统属性-Djava.awt.headless 模式
1. 什么是 java.awt.headless? Headless模式是系统的一种配置模式.在系统可能缺少显示设备.键盘或鼠标这些外设的情况下可以使用该模式. 2. 何时使用和headless mo ...
- idea搭建简单ssm框架的最详细教程（新）
为开发一个测试程序,特搭建一个简单的ssm框架,因为网上看到很多都是比较老旧的教程,很多包都不能用了,eclipes搭建并且其中还附带了很多的其他东西,所以特此记录一下mac中idea搭建过程. 另: ...