Codeforces Round #304 (Div. 2)(CF546E) Soldier and Traveling（最大流）

题意

给定 n 个城市，m 条边。人只能从走相邻边相连（只能走一次）的城市。

现在给你初始城市的每一个人数，再给一组每个城市人数。询问是否可以从当前人数变换到给定人数。如果能，输入“YES”并输出方案，不能则输出“NO”。

http://codeforces.com/contest/546/problem/E

思路

当∑a!=∑b时，肯定不能。

建一个超级源点s和超级汇点t，s到(1_{n)连一条容量为a[i]的边，(n+1}2*n)到t连一条容量为b[i]的边，再将图中给定相连的边连容量为inf的边，比如u和v相连，那么u到v+n和v到u+n都要连容量为inf的边。还要将自己跟自己连边，即i到i+n连一条容量为inf的边，因为自己点的人不走相当于自己点走到自己点。最后都连上反向边用Dinic跑最大流，如果最大流==∑a，那么能，方案可以根据i到i+n的反向边的流量来求解。

样例的建图类似下面这样（随便画的）：

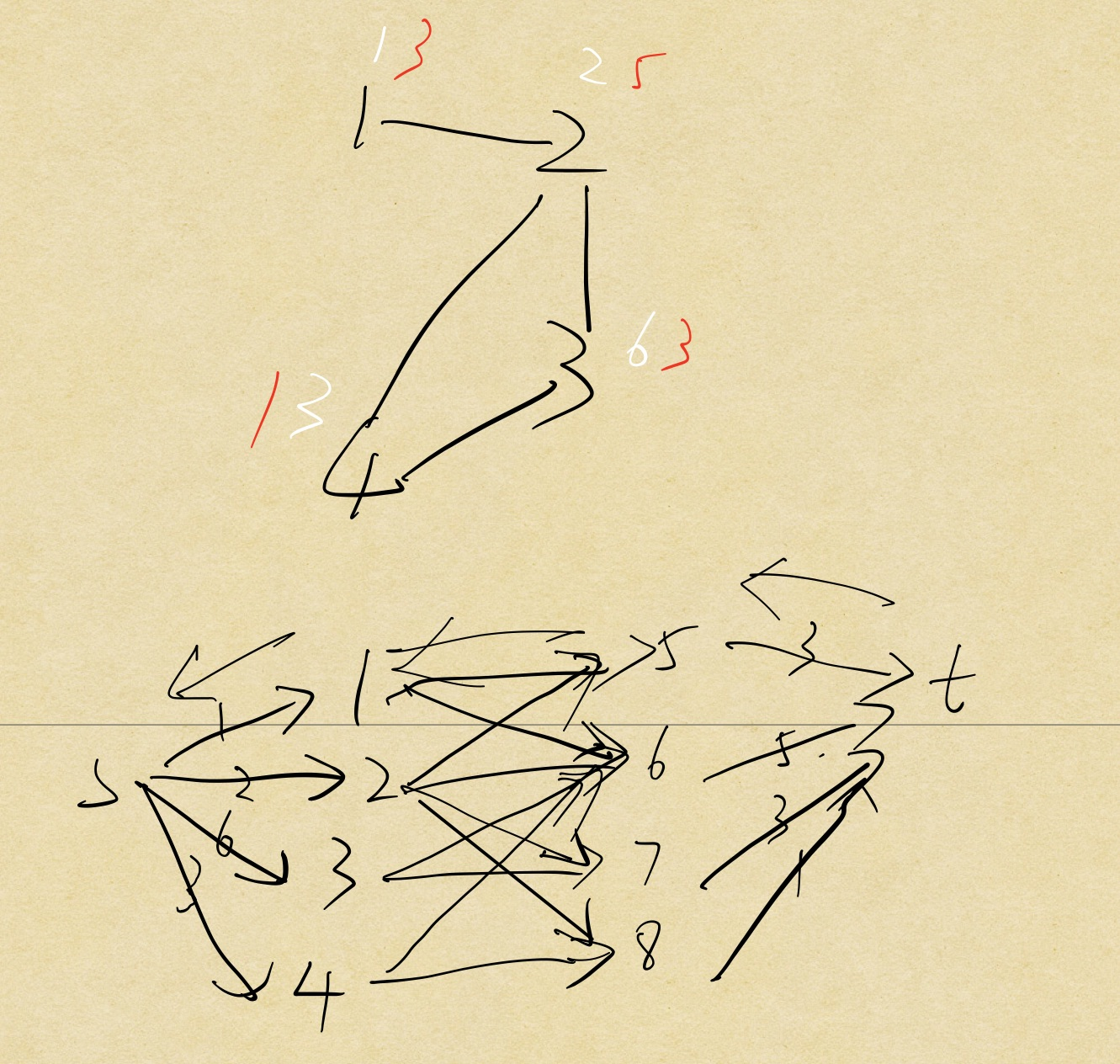
代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int inf=1e9;
const int N=505;
int n,m,x,y,z,maxflow,deep[N];//deep深度
struct Edge
{
    int next,to,dis;
} edge[N*10];
int num_edge=-1,head[N],cur[N];//cur用于复制head
queue <int> q;

void add_edge(int from,int to,int dis,bool flag)
{
    edge[++num_edge].next=head[from];
    edge[num_edge].to=to;
    if (flag) edge[num_edge].dis=dis;//反图的边权为 0
    head[from]=num_edge;
}

//bfs用来分层
bool bfs(int s,int t)
{
    memset(deep,0x7f,sizeof(deep));
    while (!q.empty()) q.pop();
    for (int i=0; i<=2*n+1; i++) cur[i]=head[i];
    deep[s]=0;
    q.push(s);

    while (!q.empty())
    {
        int now=q.front();
        q.pop();
        for (int i=head[now]; i!=-1; i=edge[i].next)
        {
            if (deep[edge[i].to]>inf && edge[i].dis)//dis在此处用来做标记 是正图还是返图
            {
                deep[edge[i].to]=deep[now]+1;
                q.push(edge[i].to);
            }
        }
    }
    if (deep[t]<inf) return true;
    else return false;
}

//dfs找增加的流的量
int dfs(int now,int t,int limit)//limit为源点到这个点的路径上的最小边权
{
    if (!limit || now==t) return limit;

    int flow=0,f;
    for (int i=cur[now]; i!=-1; i=edge[i].next)
    {
        cur[now]=i;
        if (deep[edge[i].to]==deep[now]+1 && (f=dfs(edge[i].to,t,min(limit,edge[i].dis))))
        {
            flow+=f;
            limit-=f;
            edge[i].dis-=f;
            edge[i^1].dis+=f;
            if (!limit) break;
        }
    }
    return flow;
}

void Dinic(int s,int t)
{
    while (bfs(s,t))
        maxflow+=dfs(s,t,inf);
}
int a[N],b[N];
int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d",&n,&m);
    int s1=0,s2=0,s=0,t=2*n+1;
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&a[i]);
        add_edge(s,i,a[i],1);
        add_edge(i,s,a[i],0);
        s1+=a[i];
    }
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&b[i]);
        add_edge(i+n,t,b[i],1);
        add_edge(t,i+n,b[i],0);
        s2+=b[i];
    }
    for (int i=1; i<=m; i++)
    {
        scanf("%d%d",&x,&y);
        add_edge(x,y+n,inf,1);
        add_edge(y+n,x,inf,0);
        add_edge(y,x+n,inf,1);
        add_edge(x+n,y,inf,0);
    }
    if(s1!=s2)
    {
        puts("NO");
        return 0;
    }
    for(int i=1;i<=n;i++)
    {
        add_edge(i,i+n,inf,1);add_edge(i+n,i,inf,0);
    }
    Dinic(s,t);
   // cout<<maxflow<<endl;
    if(maxflow==s1)
    {
        puts("YES");
        int g[N][N];
        for(int i=1;i<=n;i++)
        {
            for(int j=head[i];~j;j=edge[j].next)
            {
                int v=edge[j].to;
                if(v>n)
                {
                    g[i][v-n]=edge[j^1].dis;
                }
            }
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                printf("%d ",g[i][j]);
            }
            puts("");
        }
    }
    else
    {
        puts("NO");
    }
    return 0;
}