[NOIP2014] 提高组 洛谷P1941 飞扬的小鸟

题目描述

Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度，让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话，便宣告失败。

为了简化问题，我们对游戏规则进行了简化和改编：

1. 游戏界面是一个长为n ，高为 m 的二维平面，其中有k 个管道（忽略管道的宽度）。

2. 小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发，到达游戏界面最右边时，游戏完成。

3. 小鸟每个单位时间沿横坐标方向右移的距离为1 ，竖直移动的距离由玩家控制。如果点击屏幕，小鸟就会上升一定高度X ，每个单位时间可以点击多次，效果叠加；

如果不点击屏幕，小鸟就会下降一定高度Y 。小鸟位于横坐标方向不同位置时，上升的高度X 和下降的高度Y 可能互不相同。

1. 小鸟高度等于0 或者小鸟碰到管道时，游戏失败。小鸟高度为 m 时，无法再上升。

现在，请你判断是否可以完成游戏。如果可以 ，输出最少点击屏幕数；否则，输出小鸟最多可以通过多少个管道缝隙。

输入输出格式

输入格式：

输入文件名为 bird.in 。

第1 行有3 个整数n ，m ，k ，分别表示游戏界面的长度，高度和水管的数量，每两个

整数之间用一个空格隔开；

接下来的n 行，每行2 个用一个空格隔开的整数X 和Y ，依次表示在横坐标位置0 ~n- 1

上玩家点击屏幕后，小鸟在下一位置上升的高度X ，以及在这个位置上玩家不点击屏幕时，

小鸟在下一位置下降的高度Y 。

接下来k 行，每行3 个整数P ，L ，H ，每两个整数之间用一个空格隔开。每行表示一

个管道，其中P 表示管道的横坐标，L 表示此管道缝隙的下边沿高度为L ，H 表示管道缝隙

上边沿的高度（输入数据保证P 各不相同，但不保证按照大小顺序给出）。

输出格式：

输出文件名为bird.out 。

共两行。

第一行，包含一个整数，如果可以成功完成游戏，则输出1 ，否则输出0 。

第二行，包含一个整数，如果第一行为1 ，则输出成功完成游戏需要最少点击屏幕数，否则，输出小鸟最多可以通过多少个管道缝隙。

输入输出样例

输入样例#1：

10 10 6
3 9
9 9
1 2
1 3
1 2
1 1
2 1
2 1
1 6
2 2
1 2 7
5 1 5
6 3 5
7 5 8
8 7 9
9 1 3

输出样例#1：

1
6

输入样例#2：

10 10 4
1 2
3 1
2 2
1 8
1 8
3 2
2 1
2 1
2 2
1   2
1 0 2
6 7 9
9 1 4
3 8 10  

输出样例#2：

0
3

说明

【输入输出样例说明】

如下图所示，蓝色直线表示小鸟的飞行轨迹，红色直线表示管道。

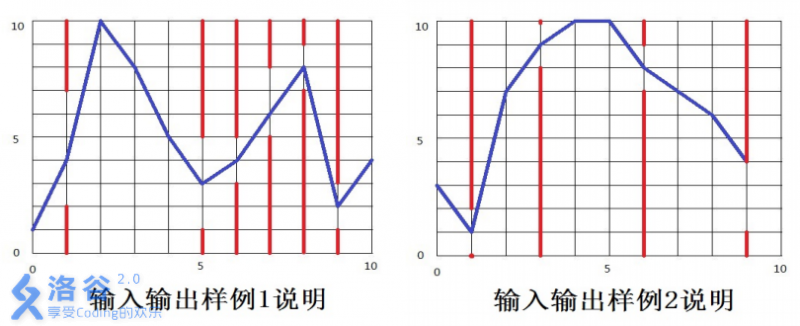
【数据范围】

对于30% 的数据：5 ≤ n ≤ 10，5 ≤ m ≤ 10，k = 0 ，保证存在一组最优解使得同一单位时间最多点击屏幕3 次；

对于50% 的数据：5 ≤ n ≤ 2 0 ，5 ≤ m ≤ 10，保证存在一组最优解使得同一单位时间最多点击屏幕3 次；

对于70% 的数据：5 ≤ n ≤ 1000，5 ≤ m ≤ 1 0 0 ；

对于100%的数据：5 ≤ n ≤ 100 0 0 ，5 ≤ m ≤ 1 0 00，0 ≤ k < n ，0<X < m ，0<Y <m，0<P <n，0 ≤ L < H ≤ m ，L +1< H 。

动态规划。

f[x][y]=到达坐标(x,y)时的最小点击数。

暴力DP，详见代码。

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 using namespace std;
 int f[][];//到达坐标[x][y]的最小点击数
 int n,m,k;
 int mv[][];//[坐标][1-点击上升；2-不点击下降]
 int p[],L[],H[];
 int main(){
     //read
     int i,j;
     scanf("%d%d%d",&n,&m,&k);
     int x,y,l,h;
     for(i=;i<n;i++){
         scanf("%d%d",&x,&y);
         mv[i][]=x;
         mv[i][]=y;
     }
     for(i=;i<=k;i++){
         scanf("%d%d%d",&x,&l,&h);
         p[x]=;
         L[x]=l;
         H[x]=h;
     }
     //finish reading
     for(i=;i<=n+;i++)
         for(j=;j<=m+;j++)f[i][j]=;
     int ct=;
     for(i=;i<=n;i++){
         //正常上飞
         for(j=mv[i-][]+;j<=m;j++){
             f[i][j]=min(f[i][j],min(f[i-][j-mv[i-][]],f[i][j-mv[i-][]])+);
         }
         //正常下降
         for(j=;j<=m-mv[i-][];j++){
             f[i][j]=min(f[i][j],f[i-][j+mv[i-][]]);
         }
         //到顶
         for(j=m-mv[i-][];j<=m;j++){
             f[i][m]=min(f[i][m],min(f[i-][j],f[i][j])+);
         }
         if(p[i]){
             for(j=;j<=L[i];j++)f[i][j]=;
             for(j=H[i];j<=m;j++)f[i][j]=;
         }
         //过柱子检测
         if(p[i])    for(j=;j<=m;j++)if(f[i][j]!=){ct++;break;};
     }
 //    printf("test 1 :%d  %d\n",n,m);
 //test
 /*    for(i=m;i>=1;i--){
         cout<<endl;
         for(j=1;j<=n;j++)printf("%-8d",f[j][i]);
         cout<<endl;
     }
 */
 //end
     int ans=;
     for(i=;i<=m;i++)
       if(f[n][i]<ans)ans=f[n][i];
     if(ans!=)printf("1\n%d",ans);
         else printf("0\n%d",ct);
     return ;
 }