uva 12096 The SetStack Computer（STL set的各种库函数 交集 并集 插入迭代器）

题意：

有5种操作：

PUSH：加入“｛｝”空集合入栈。

DUP：栈顶元素再入栈。

UNION：出栈两个集合，取并集入栈。

INTERSECT：出栈两个集合，取交集入栈。

ADD：出栈两个集合，将先出栈的加入到后出栈的集合中。

输入不超过2000， 保证操作顺利进行。

分析：

用set<int>(本身又可以映射成一个int)去模拟集合，所以可以将不同的集合映射成int型。

用一个Map<set<int>,int> 去映射成不同的int。

以后需要set做交集并集的时候再从map中拿出set做操作再映射，有点复杂，需要慢慢体会这种映射的方法。

代码有两个难点：

1.插入迭代器：

http://www.cnblogs.com/Jadon97/p/6884067.html

2.set_union() , set_intersection.

首先元素在内部要排好序，set显然满足这一点。

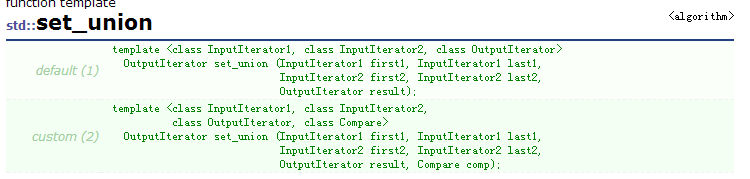
代码参考刘汝佳第五章例题

 #include <iostream>
 #include <cstring>
 #include <cstdio>
 #include <set>
 #include <vector>
 #include <string>
 #include <map>
 #include <queue>
 #include <stack>
 #include <algorithm>
 #include <sstream>

 #define ALL(x) x.begin(),x.end()
 #define INS(x) inserter(x,x.begin())
 using namespace std;
 typedef set<int> Set;
 map<Set, int> IDcache;
 vector<Set> Setcache;
 int ID (Set x)
 {
     if(IDcache.count(x)) return IDcache[x];
     Setcache.push_back(x);
     return IDcache[x] = Setcache.size() - ; //都是空集， 唯一区别就是大小
 }
 int main()
 {
 //    freopen("1.txt","r",stdin);
     int t;
     cin>>t;
     while(t--)
     {
         IDcache.clear();
         Setcache.clear();
         stack<int> s;
         int n;
         cin>>n;
         for(int i =  ; i < n ; i++)
         {
             string op;
             cin >> op;
             if(op[] == 'P')
                s.push(ID(Set()));
             else if(op[] == 'D')
                 s.push(s.top());
             else
             {
                 Set x1 = Setcache[s.top()];
                 s.pop();
                 Set x2 = Setcache[s.top()];
                 s.pop();
                 Set x;
                 if(op[] == 'U') set_union(ALL(x1),ALL(x2),INS(x));
                 if(op[] == 'I') set_intersection(ALL(x1), ALL(x2), INS(x));
                 if(op[] == 'A')
                 {
                     x=x2;
                     x.insert(ID(x1));
                 }
                 s.push(ID(x));
             }
              cout<< Setcache[s.top()].size() <<endl;
         }
         cout<<"***"<<endl;
     }
 }