洛谷 P1081 开车旅行（70）

P1081 开车旅行

题目描述

小AA 和小BB 决定利用假期外出旅行，他们将想去的城市从 11到 NN 编号，且编号较小的城市在编号较大的城市的西边，已知各个城市的海拔高度互不相同，记城市 ii的海拔高度为H_iHi​，城市 ii和城市jj之间的距离 d_[i,j]d[​i,j]恰好是这两个城市海拔高度之差的绝对值，即d_[i,j]=|H_i-H_j|d[​i,j]=∣Hi​−Hj​∣。

旅行过程中，小 AA和小 BB 轮流开车，第一天小 AA 开车，之后每天轮换一次。他们计划选择一个城市 SS 作为起点，一直向东行驶，并且最多行驶XX 公里就结束旅行。小AA 和小 BB的驾驶风格不同，小 BB总是沿着前进方向选择一个最近的城市作为目的地，而小AA总是沿着前进方向选择第二近的城市作为目的地（注意：本题中如果当前城市到两个城市的距离相同，则认为离海拔低的那个城市更近）。如果其中任何一人无法按照自己的原则选择目的城市，或者到达目的地会使行驶的总距离超出 XX 公里，他们就会结束旅行。

在启程之前，小 AA想知道两个问题：

1. 对于一个给定的 X=X_0X=X0​，从哪一个城市出发，小AA 开车行驶的路程总数与小BB 行驶的路程总数的比值最小（如果小 BB 的行驶路程为00，此时的比值可视为无穷大，且两个无穷大视为相等）。如果从多个城市出发，小AA 开车行驶的路程总数与小 BB行驶的路程总数的比值都最小，则输出海拔最高的那个城市。
2. 对任意给定的 X=X_iX=Xi​和出发城市S_iSi​，小 AA 开车行驶的路程总数以及小 BB行驶的路程总数。

输入输出格式

输入格式：

第一行包含一个整数 NN，表示城市的数目。

第二行有 NN个整数，每两个整数之间用一个空格隔开，依次表示城市 11 到城市NN的海拔高度，即 H_1,H_2,…,H_nH1​,H2​,…,Hn​，且每个 H_iHi​都是不同的。

第三行包含一个整数X_0X0​。

第四行为一个整数 MM，表示给定 MM组 S_iSi​和X_iXi​。

接下来的 MM 行，每行包含 22 个整数 S_iSi​和 X_iXi​，表示从城市S_iSi​出发，最多行驶 X_iXi​公里。

输出格式：

输出共M+1M+1行。

第一行包含一个整数 S_0S0​，表示对于给定的 X_0X0​，从编号为 S_0S0​ 的城市出发，小 AA开车行驶的路程总数与小BB 行驶的路程总数的比值最小。

接下来的 MM行，每行包含22 个整数，之间用一个空格隔开，依次表示在给定的 S_iSi​和X_iXi​下小 AA 行驶的里程总数和小 BB 行驶的里程总数。

输入输出样例

输入样例#1： 复制

4
2 3 1 4
3
4
1 3
2 3
3 3
4 3

输出样例#1： 复制

1
1 1
2 0
0 0
0 0 

输入样例#2： 复制

10
4 5 6 1 2 3 7 8 9 10
7
10
1 7
2 7
3 7
4 7
5 7
6 7
7 7
8 7
9 7
10 7

输出样例#2： 复制

2
3 2
2 4
2 1
2 4
5 1
5 1
2 1
2 0
0 0
0 0

说明

【输入输出样例1说明】

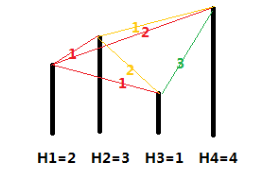
各个城市的海拔高度以及两个城市间的距离如上图所示。

如果从城市 11 出发，可以到达的城市为 2,3,42,3,4，这几个城市与城市 11 的距离分别为 1,1,21,1,2，但是由于城市 33 的海拔高度低于城市 22，所以我们认为城市 33 离城市 11 最近，城市 22 离城市 11 第二近，所以小A会走到城市22。到达城市22后，前面可以到达的城市为3,43,4，这两个城市与城市22的距离分别为2,12,1，所以城市44离城市22最近，因此小B会走到城市44。到达城市44后，前面已没有可到达的城市，所以旅行结束。

如果从城市 22 出发，可以到达的城市为 3,43,4，这两个城市与城市22的距离分别为 2,12,1，由于城市 33 离城市 22 第二近，所以小A会走到城市33。到达城市33后，前面尚未旅行的城市为44，所以城市44离城市33最近，但是如果要到达城市44，则总路程为 2+3=5>32+3=5>3，所以小B会直接在城市33结束旅行。

如果从城市 33 出发，可以到达的城市为 44，由于没有离城市33第二近的城市，因此旅行还未开始就结束了。

如果从城市 44 出发，没有可以到达的城市，因此旅行还未开始就结束了。

【输入输出样例2说明】

当 X=7X=7 时，如果从城市 11 出发，则路线为1 \to 2 \to 3 \to 8 \to 91→2→3→8→9，小A走的距离为1+2=31+2=3，小B走的距离为1+1=21+1=2。（在城市11时，距离小A最近的城市是22和66，但是城市22的海拔更高，视为与城市11第二近的城市，所以小A最终选择城市22；走到99后，小A只有城市1010可以走，没有第22选择可以选，所以没法做出选择，结束旅行）

如果从城市22出发，则路线为2 \to 6 \to 72→6→7，小A和小B走的距离分别为2,42,4。

如果从城市33出发，则路线为3 \to 8 \to 93→8→9，小A和小B走的距离分别为2,12,1。

如果从城市44出发，则路线为4 \to 6 \to 74→6→7，小A和小B走的距离分别为2,42,4。

如果从城市55出发，则路线为5 \to 7 \to 85→7→8，小A和小B走的距离分别为5,15,1。

如果从城市66出发，则路线为6 \to 8 \to 96→8→9，小A和小B走的距离分别为5,15,1。

如果从城市77出发，则路线为7 \to 9 \to 107→9→10，小A和小B走的距离分别为2,12,1。

如果从城市88出发，则路线为8 \to 108→10，小A和小B走的距离分别为2,02,0。

如果从城市99出发，则路线为99，小A和小B走的距离分别为0,00,0（旅行一开始就结束了）。

如果从城市1010出发，则路线为1010，小A和小B走的距离分别为0,00,0。

从城市22或者城市44出发小A行驶的路程总数与小B行驶的路程总数的比值都最小，但是城市22的海拔更高，所以输出第一行为22。

【数据范围与约定】

对于30%的数据，有1≤N≤20,1≤M≤201≤N≤20,1≤M≤20；
对于40%的数据，有1≤N≤100,1≤M≤1001≤N≤100,1≤M≤100；
对于50%的数据，有1≤N≤100,1≤M≤1,0001≤N≤100,1≤M≤1,000；
对于70%的数据，有1≤N≤1,000,1≤M≤10,0001≤N≤1,000,1≤M≤10,000；
对于100%的数据，有1≤N≤100,000,1≤M≤100,0001≤N≤100,000,1≤M≤100,000, -10^9≤H_i≤10^9−109≤Hi​≤109, 0≤X_0≤10^90≤X0​≤109, 1≤S_i≤N,0≤X-i≤10^91≤Si​≤N,0≤X−i≤109，数据保证H_iHi​互不相同。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 100010
using namespace std;
int n,m,ans;
long long x0;
long long map[MAXN][][];
long long h[MAXN],dis[MAXN];
struct nond{ int id;long long dis,H; }v[MAXN];
bool cmp(nond a,nond b){
    if(a.dis==b.dis)    return a.H<b.H;
    return a.dis<b.dis;
}
void pre(){
    memset(map,-,sizeof(map));
    for(int i=;i<=n;i++){
        int tot=;
        for(int j=i+;j<=n;j++){
            tot+=;
            v[tot].id=j;v[tot].H=h[j];
            v[tot].dis=abs(h[i]-h[j]);
        }
        sort(v+,v++tot,cmp);
        map[i][][]=v[].dis;map[i][][]=v[].dis;
        map[i][][]=v[].id;map[i][][]=v[].id;
        memset(v,-,sizeof(v));
    }
}
void work1(){
    double minn=1e9+,hh=-,flag=;
    for(int i=;i<=n;i++){
        long long peo=,pos=i,sa=,sb=;
        while(){
            peo%=;
            if(peo==){
                if(map[pos][][]+sa+sb>x0||map[pos][][]==-)    break;
                peo+=;sa+=map[pos][][];
                pos=map[pos][][];flag=;
            }
            else if(peo==){
                if(map[pos][][]+sa+sb>x0||map[pos][][]==-)    break;
                peo+=;sb+=map[pos][][];
                pos=map[pos][][];flag=;
            }
        }
        if(sb==)    continue;
        double tmp=(sa*1.0)/(sb*1.0);
        if(tmp<minn){ minn=tmp;ans=i;hh=h[i]; }
        else if(tmp==minn&&h[i]>hh)    ans=i,hh=h[i];
    }
    if(minn==1e9+&&flag==){
        minn=;
        for(int i=;i<=n;i++)
            if(h[i]>minn){
                minn=h[i];
                ans=i;
            }
    }
    cout<<ans<<endl;
}
void work2(int pos,int x){
    long long sa=,sb=,peo=;
    while(){
        peo%=;
        if(peo==){
            if(map[pos][][]+sa+sb>x||map[pos][][]==-)    break;
            peo+=;sa+=map[pos][][];
            pos=map[pos][][];
        }
        else if(peo==){
            if(map[pos][][]+sa+sb>x||map[pos][][]==-)    break;
            peo+=;sb+=map[pos][][];
            pos=map[pos][][];
        }
    }
    cout<<sa<<" "<<sb<<endl;
}
int main(){
    freopen("drive.in","r",stdin);
    freopen("drive.out","w",stdout);
    scanf("%d",&n);
    for(int i=;i<=n;i++)
        scanf("%lld",&h[i]);
    scanf("%lld",&x0);
    pre();
    work1();
    scanf("%d",&m);
    for(int i=;i<=m;i++){
        long long s,x;
        scanf("%lld%lld",&s,&x);
        work2(s,x);
    }
}
/*
5
-1000000000 0 -999999999 999999999 1000000000
1000000000
7
1 1000000000
2 1000000000
3 1000000000
4 1000000000
5 1000000000
1 2
2 3
*/

70分暴力