POJ 1038 Bug Integrated Inc(状态压缩DP)

Description

Bugs Integrated, Inc. is a major manufacturer of advanced memory chips. They are launching production of a new six terabyte Q-RAM chip. Each chip consists of six unit squares arranged in a form of a 2*3 rectangle. The way Q-RAM chips are made is such that one takes a rectangular plate of silicon divided into N*M unit squares. Then all squares are tested carefully and the bad ones are marked with a black marker. 

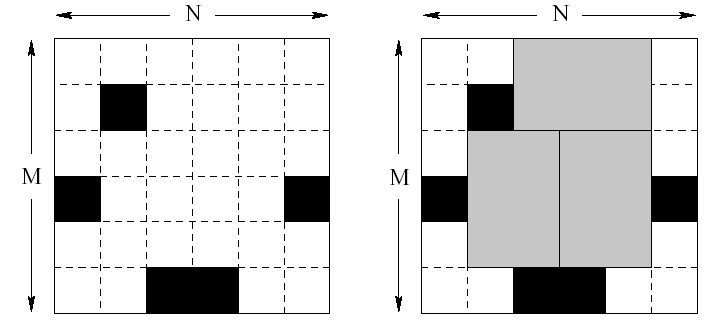
Finally, the plate of silicon is cut into memory chips. Each chip consists of 2*3 (or 3*2) unit squares. Of course, no chip can contain any bad (marked) squares. It might not be possible to cut the plate so that every good unit square is a part of some memory chip. The corporation wants to waste as little good squares as possible. Therefore they would like to know how to cut the plate to make the maximum number of chips possible. 
Task 
You are given the dimensions of several silicon plates and a list of all bad unit squares for each plate. Your task is to write a program that computes for each plate the maximum number of chips that can be cut out of the plate.

Input

The first line of the input file consists of a single integer D (1 <= D <= 5), denoting the number of silicon plates. D blocks follow, each describing one silicon plate. The first line of each block contains three integers N (1 <= N <= 150), M (1 <= M <= 10), K (0 <= K <= MN) separated by single spaces. N is the length of the plate, M is its height and K is the number of bad squares in the plate. The following K lines contain a list of bad squares. Each line consists of two integers x and y (1 <= x <= N, 1 <= y <= M) ?coordinates of one bad square (the upper left square has coordinates [1, 1], the bottom right is [N,M]).

Output

For each plate in the input file output a single line containing the maximum number of memory chips that can be cut out of the plate.

Sample Input

2
6 6 5
1 4
4 6
2 2
3 6
6 4
6 5 4
3 3
6 1
6 2
6 4

Sample Output

3
4

思路:

1. 允许的内存为 30000K, 需要使用滚动数组

2. dp[row][state], row 实际取值只有0,1, 使用滚动数组递推, 表示 row, row-1 行的状态为 state 时的最优解(最多的矩形数)

state 一个变量就标出来两行的状态

3. dp[row][state] 由 row, row-1, row-2 三行决定.

　　<1>　　row 行的 l 列不可以是坏点

　　<2>　　若是 3*2 的摆放方式, 则 row-1 行, row-2 行, l, l+1, 列不可以被占据

　　<3>　　若是 2*3 ...

void dfs(const int &row, const int &pos, const int &maxNum, const int &s) {
	dp[row%2][s] = max(dp[row%2][s], maxNum); // 继承
	if(pos >= M) return; // 步长不是1, 所以 == 不行
	if(pos<M && !stateCur[pos] && !stateCur[pos+1] && !statePre[pos] && !statePre[pos+1]) {
		// 3*2 的矩形
		stateCur[pos] = stateCur[pos+1] = 2; // 对下一层来讲, 只需要 stateCur
		int k = tri2Ten(stateCur);
		dfs(row, pos+2, maxNum+1, k);
		stateCur[pos] = stateCur[pos+1] = 0; // 还原
	}
	if(pos<M-1 && !stateCur[pos] && !stateCur[pos+1] && !stateCur[pos+2]) {
		stateCur[pos] = stateCur[pos+1] = stateCur[pos+3] = 2;
		int k = tri2Ten(stateCur);
		dfs(row, pos+3, maxNum+1, k);
		stateCur[pos] = stateCur[pos+1] = stateCur[pos+3] = 0;
	}
	dfs(row, pos+1, maxNum, s);
}

　　

总结:

1. map[0] 可初始化为全部被占据. 并且, 这也不需要显式赋值, 只需

for(int i = 0; i <= M; i ++)
    statePre[i] = map[1][i] + 1;

2. 代码中的 dfs 函数很是精髓. row 是可以当做全局变量, 不需要显式的当做参数. pos 和 maxNum 是必须的, s 主要是为了更新 dp[row%2][s]

3. 最后一步 ans = max(ans, dp[row%2][i]), 可以通过观察发现 row%2 总是最后一行

代码:

#include <iostream>
using namespace std;

const int MAXN = 60000;
int tri[12]={0,1,3,9,27,81,243,729,2187,6561,19683,59049};  // 三进制
int testCase, N, M, K;
int statePre[11], stateCur[11];
int map[160][11];
int dp[2][MAXN];

void ten2Tri(int j) {
	memset(statePre, 0, sizeof(statePre));
	for(int i = 1; i <= M && j; i ++) {
		statePre[i] = j % 3;
		j /= 3;
	}
}
int tri2Ten(const int *p) {
	int ans = 0;
	for(int i = 1; i <= M; i ++) {
		ans += (p[i]*tri[i]);
	}
	return ans;
}
void pre_process() {
	memset(statePre, 0, sizeof(statePre));
	memset(stateCur, 0, sizeof(stateCur));
	// 初始化第一列 state, 假设第 0 列全被占据
	memset(dp, -1, sizeof(dp));
	for(int i = 1; i <= M; i ++)
		statePre[i] = map[1][i] + 1;

	dp[1][tri2Ten(statePre)] = 0;
	//cout << tri2Ten(statePre)  << endl;
}
/*
 *	搜寻出每一行所有可能的摆放方式
 *	限制条件是该行不可以有坏点
 *	需要同时得出所有的 state 值
 */
void dfs(const int &row, const int &pos, const int &maxNum, const int &s) {
	dp[row%2][s] = max(dp[row%2][s], maxNum); // 继承
	if(pos >= M) return; // 步长不是1, 所以 == 不行
	if(pos<M && !stateCur[pos] && !stateCur[pos+1] && !statePre[pos] && !statePre[pos+1]) {
		// 3*2 的矩形
		stateCur[pos] = stateCur[pos+1] = 2; // 对下一层来讲, 只需要 stateCur
		int k = tri2Ten(stateCur);
		dfs(row, pos+2, maxNum+1, k);
		stateCur[pos] = stateCur[pos+1] = 0; // 还原
	}
	if(pos<M-1 && !stateCur[pos] && !stateCur[pos+1] && !stateCur[pos+2]) {
		stateCur[pos] = stateCur[pos+1] = stateCur[pos+2] = 2;
		int k = tri2Ten(stateCur);
		dfs(row, pos+3, maxNum+1, k);
		stateCur[pos] = stateCur[pos+1] = stateCur[pos+2] = 0;
	}
	dfs(row, pos+1, maxNum, s);
}

int mainFunc() {
	for(int row = 2; row <= N; row++) {
		for(int j = 0; j < tri[M+1]; j ++) { // 所有可能状态 j
			dp[row%2][j] = -1;
		}
		for(int j = 0; j < tri[M+1]; j++) { // 上一行的所有可能状态 j
			if(dp[(row+1)%2][j] == -1)	// 无法用来更新, 没有利用价值, 直接跳过
				continue;
			ten2Tri(j);	// 获得 statePre
			for(int l = 1; l <= M; l ++) {
				if(map[row][l])
					stateCur[l] = 2;
				else
					stateCur[l] = max(0, statePre[l]-1);
			}
			int pass = dp[(row+1)%2][j];
			dfs(row, 1, pass, tri2Ten(stateCur));
		}
	}
	int ans = 0;
	for(int i = 0; i < tri[M+1]; i ++)
		ans = max(ans, dp[N%2][i]);
	return ans;
}
int main() {
	freopen("E:\\Copy\\test\\in.txt", "r", stdin);
	cin >> testCase;
	while(testCase--) {
		cin >> N >> M >> K;
		memset(map, 0, sizeof(map));
		for(int i = 1; i <= K; i ++) {
			int a, b;
			scanf("%d%d", &a, &b);
			map[a][b] = 1;
		}
		pre_process();
		cout << mainFunc() << endl;
	}
	return 0;
}