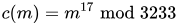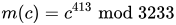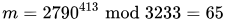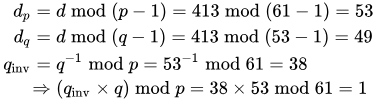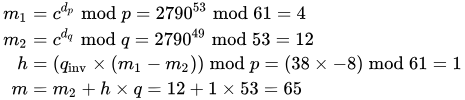Chinese_remainder_theorem
https://en.wikipedia.org/wiki/Chinese_remainder_theorem
中国剩余定理
https://en.wikipedia.org/wiki/RSA_(cryptosystem)
The public key is (n = 3233, e = 17). For a padded plaintext message m, the encryption function is
The private key is (n = 3233, d = 413). For an encrypted ciphertext c, the decryption function is
For instance, in order to encrypt m = 65, we calculate
To decrypt c = 2790, we calculate
Both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation. In real-life situations the primes selected would be much larger; in our example it would be trivial to factor n, 3233 (obtained from the freely available public key) back to the primes p and q. e, also from the public key, is then inverted to get d, thus acquiring the private key.
Practical implementations use the Chinese remainder theorem to speed up the calculation using modulus of factors (mod pq using mod p and mod q).
The values dp, dq and qinv, which are part of the private key are computed as follows:
Here is how dp, dq and qinv are used for efficient decryption. (Encryption is efficient by choice of a suitable d and e pair)
Chinese_remainder_theorem的更多相关文章
- CODEVS.3990.中国余数定理2(CRT)
题目链接 颓了一天 写个模板吧.. Chinese_Remainder_Theorem: MashiroSky.远航之曲 #include <cstdio> #include <cc ...
- 【10.4校内测试】【轮廓线DP】【中国剩余定理】【Trie树+博弈】
考场上几乎是一看就看出来轮廓线叻...可是调了两个小时打死也过不了手出样例!std发下来一对,特判对的啊,转移对的啊,$dp$数组竟然没有取max!!! 某位考生当场死亡. 结果下午又请了诸位dala ...
- NOIP数学相关模板整理
$O(n)$递推求逆元 #include<cstdio> #include<cstring> #include<algorithm> using namespace ...
- Chinese remainder theorem
https://en.wikipedia.org/wiki/Chinese_remainder_theorem http://planetmath.org/ChineseRemainderTheore ...
- 第三十三个知识点:Bellcore攻击是如何攻击使用CRT的RSA的?
第三十三个知识点:Bellcore攻击是如何攻击使用CRT的RSA的? 注意:这篇博客是由follow论密码计算中消除错误的重要性(On the importance of Eliminating E ...
随机推荐
- 类加载器详解 (转至http://blog.csdn.net/jiangwei0910410003/article/details/17733153)
首先来了解一下字节码和class文件的区别: 我们知道,新建一个java对象的时候,JVM要将这个对象对应的字节码加载到内存中,这个字节码的原始信息存放在classpath(就是我们新建Java工程的 ...
- mysqldump进行数据库的全备时,备份数据库的顺序是什么,就是先备份哪个库,然后再备份哪个库
需求描述: 今天在用mysqldump工具进行数据库的备份的时候,突然想了一个问题,比如我有10个库要进行备份 那么是先备份哪个,然后再备份哪个呢,所以,做了实验,验证下. 操作过程: 1.使用--a ...
- 创建ros的程序包--3
创建ros的程序包(原创博文,转载请标明出处--周学伟http://www.cnblogs.com/zxouxuewei/) 1.一个catkin程序包由什么组成? 一个程序包要想称为catkin程序 ...
- 请问C#中string是值传递还是引用传递?
https://www.cnblogs.com/xiangniu/archive/2011/08/17/2143486.html 学了这么久,终于弄明白了... 是引用传递 但是string又有值传递 ...
- linq select
var categoryIdArray = MusicCategoryRelationBLL.GetModel(music.Id); music.MusicCategoryIds = string.E ...
- Webservice简单案例
东西不用,时间长了就会被忘掉.重新拾起来 做一个简单的Demo,便于以后的查询 服务器端--新建Calculator.asmx using System; using System.Collectio ...
- C语言中的文本流与二进制流的区别
近期看到了文本流和二进制流的区别,书上讲的比较含糊,理解不透彻,于是细细琢磨了下,把心得跟大家分享一下: 一.首先回答,什么是文件,流 一个文件通常就是磁盘上的一段命名的存储区.比如 stdio.h ...
- Nginx 0.8.x + PHP 5.2.13(FastCGI)搭建胜过Apache十倍的Web服务器[摘抄]
[文章作者:张宴 本文版本:v6.3 最后修改:2010.07.26 转载请注明原文链接:http://blog.s135.com/nginx_php_v6/] 前言:本文是我撰写的关于搭建“Ngin ...
- PyQt4 菜单栏 + 工具栏 + 状态栏 + 中心部件 生成一个文本编辑部件示例
我们将创建一个菜单栏.一个工具栏.一个状态栏和一个中心部件. #!/usr/bin/python # -*- coding:utf-8 -*- import sys from PyQt4 import ...
- Android 手机随音乐振动
想到做一个Android软件可以在播放音乐的同时手机在音量或者音调高的时候振动一下. 等我熟练Android的时候试试...