POJ 3347 Kadj Squares （计算几何+线段相交）

题意：从左至右给你n个正方形的边长，接着这些正方形都按照旋转45度以一角为底放置坐标轴上，最左边的正方形左端点抵住y轴，后面的正方形依次紧贴前面所有正方形放置，问从上方向下看去，有哪些正方形是可以被看到的（如图）

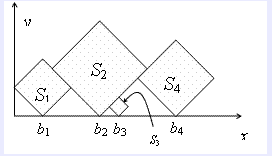
题解：首先找到每个正方形左右端点的坐标转化为一条线段，接着寻找哪些线段被其他某些条线段覆盖，那这些被覆盖的线段就不能被看到了

寻找被覆盖的线段利用区间贪心，我们按照左端点升序、左端点相同右端点降序排序，则左端点一定被前面的线段覆盖，接着对于右端点使用单调栈的思想寻找可以看到的线段就好

找左端点时就将此正方形与之前的每个正方形紧贴找最大的值（关键）

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<vector>
#include<string>
#include<cstdio>
#include<cstring>
#include<iomanip>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1E-8
/*注意可能会有输出-0.000*/
#define Sgn(x) (x<-eps? -1 :x<eps? 0:1)//x为两个浮点数差的比较,注意返回整型
#define Cvs(x) (x > 0.0 ? x+eps : x-eps)//浮点数转化
#define zero(x) (((x)>0?(x):-(x))<eps)//判断是否等于0
#define mul(a,b) (a<<b)
#define dir(a,b) (a>>b)
typedef long long ll;
typedef unsigned long long ull;
const int Inf=<<;
const ll INF=1ll<<;
const double Pi=acos(-1.0);
const int Mod=1e9+;
const int Max=;
int num[Max],vis[Max];
int line[Max];
struct node
{
    int x,y,pos;
} lin[Max];
bool cmp(node a,node b)
{
    if(a.x==b.x)
        return a.y>b.y;
    return a.x<b.x;
}
int Jud(int n)
{
    int coun=;
    for(int i=; i<n; ++i)
    {
         lin[i].x=line[i],lin[i].y=line[i]+num[i],lin[i].pos=i+;
    }
    sort(lin,lin+n,cmp);
    vis[coun++]=;
    node now=lin[];
    for(int i=;i<n;++i)
    {
        if(lin[i].y>now.y)
        {
            for(int j=coun-;j>=;--j)
            {
                 if(lin[i].x<=lin[vis[j]].y)//找之前的lin（不一定连续）
                coun--;
            else
                break;
            }
             now=lin[i];
            vis[coun++]=i;//注意这儿记录的值
        }
    }
    for(int i=;i<coun;++i)
        vis[i]=lin[vis[i]].pos;
    sort(vis,vis+coun);
    return coun;
}
int main()
{
    int n;
    while(~scanf("%d",&n)&&n)
    {
        for(int i=; i<n; ++i)
        {
            scanf("%d",&num[i]);
            num[i]*=;//边长变成对角线，但是同比例扩大sqrt(2.0)后就变成2倍了
        }
        line[]=;
        for(int i=; i<n; ++i)
        {
            line[i]=;
            for(int j=; j<i; ++j)
            {
                int tem=num[j]-abs(num[i]-num[j])/+line[j];//与每个之前的正方形紧贴在一起的x轴坐标
                line[i]=max(line[i],tem);//一定是x轴最大的值
            }
        }
        int coun=Jud(n);
        for(int i=; i<coun; ++i)
            printf("%d%c",vis[i],i==coun-?'\n':' ');
    }
    return ;
}