有限差分法解矩形波导内场值、截止频率 MATLAB

利用有限差分法，解矩形波导内场解和截止频率：

这里以解TM11模为例，利用双重迭代法，每4次场值，更新一次Kc：

%%
%   求矩形波导中TM11模 截面内场分布、截止频率kc和特性阻抗Zc
%   //
%
%% Init
clear; clc
w = 1.5;            %收敛因子
count = ;         %迭代次数
xa = ; xb = ;   %矩阵长宽度
h = pi / ;
aa = h*(xa-); bb = h*(xb-);

%% 赋初值
% 内点初值
for i =  : (xa-)
    for j =  : (xb - )
        u(i, j) = 1.15;
    end
end

% 边的初值
u(,:) = ; u(,:) = ;
u(:,) = ; u(:,) = ;

% kc初值
kc = 0.15;

%% 迭代更新
k = ; k2 = ;
sum1 = ; sum2 = ; sum = ;

while k < count
    for i =  : xa-
        for j =  : xb-
               u(i,j) = u(i,j) + w*((u(i+,j)+u(i,j+)+u(i-,j)+u(i,j-))/(-(kc*h)^) -u(i,j));
        end
    end
    k = k + ;
    k2 = k2 + ;

    if(rem(k2,) == )
        for i =  : xa-
            for j =  : xb-
                sum1 = sum1+ u(i,j)*(u(i+,j)+u(i,j+)+u(i-,j)+u(i,j-)-*u(i,j));
                sum2 = sum2 + u(i,j)^;
            end
        end
        kc = sqrt(-sum1/sum2)/h;
    end
end

%% 结果展示
surf(u);
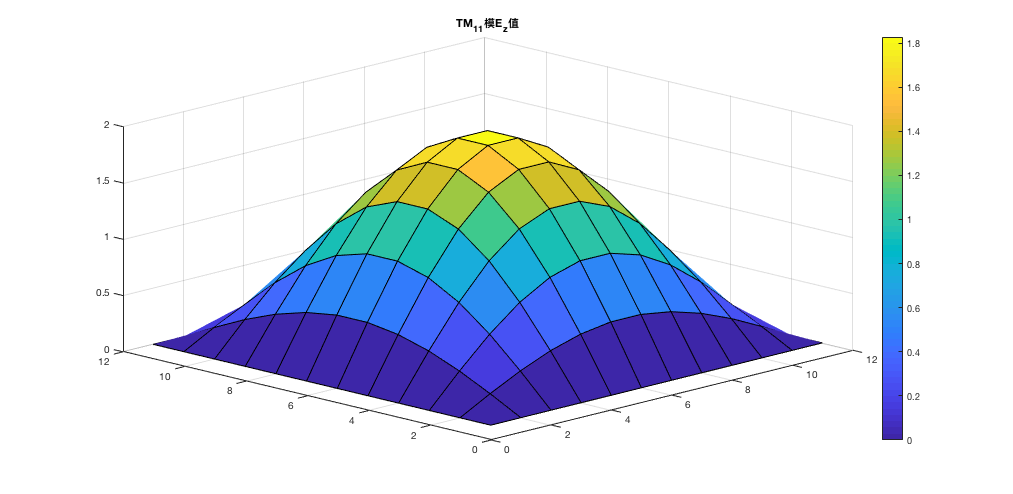
title('TM_{11}模E_z值');
colorbar

c =  * ^;
fc = c * kc /(*pi*^)

kc
kc0 = sqrt((pi/aa)^+(pi/bb)^)
max(max(u))

最后效果如图所示：