【POJ 2750】 Potted Flower（线段树套dp）

【POJ 2750】 Potted Flower（线段树套dp）

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 4566		Accepted: 1739

Description

The little cat takes over the management of a new park. There is a large circular statue in the center of the park, surrounded by N pots of flowers. Each potted flower will be assigned to an integer number (possibly negative) denoting
how attractive it is. See the following graph as an example:



(Positions of potted flowers are assigned to index numbers in the range of 1 ... N. The i-th pot and the (i + 1)-th pot are consecutive for any given i (1 <= i < N), and 1st pot is next to N-th pot in addition.)








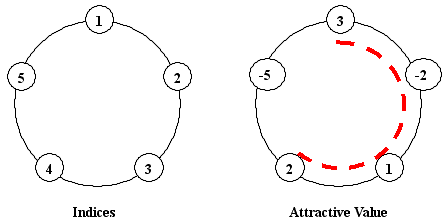
The board chairman informed the little cat to construct "ONE arc-style cane-chair" for tourists having a rest, and the sum of attractive values of the flowers beside the cane-chair should be as large as possible. You should notice that a cane-chair cannot be
a total circle, so the number of flowers beside the cane-chair may be 1, 2, ..., N - 1, but cannot be N. In the above example, if we construct a cane-chair in the position of that red-dashed-arc, we will have the sum of 3+(-2)+1+2=4, which is the largest among
all possible constructions.



Unluckily, some booted cats always make trouble for the little cat, by changing some potted flowers to others. The intelligence agency of little cat has caught up all the M instruments of booted cats' action. Each instrument is in the form of "A B", which means
changing the A-th potted flowered with a new one whose attractive value equals to B. You have to report the new "maximal sum" after each instruction.

Input

There will be a single test data in the input. You are given an integer N (4 <= N <= 100000) in the first input line.




The second line contains N integers, which are the initial attractive value of each potted flower. The i-th number is for the potted flower on the i-th position.



A single integer M (4 <= M <= 100000) in the third input line, and the following M lines each contains an instruction "A B" in the form described above.



Restriction: All the attractive values are within [-1000, 1000]. We guarantee the maximal sum will be always a positive integer.

Output

For each instruction, output a single line with the maximum sum of attractive values for the optimum cane-chair.

Sample Input

5
3 -2 1 2 -5
4
2 -2
5 -5
2 -4
5 -1

Sample Output

4
4
3
5

Source

POJ Monthly--2006.01.22,Zeyuan Zhu

不知道这样说够不够准确 总的来说就是把dp的思想加到了线段树中。

在我感觉肯定能A的时候给我了个WA 在我万念俱灰的时候给我了个AC。。。

首先依据题目 n个点构成的环 要求求出最大的连续子序列 n与1是相邻的(环的性质)

仅仅到这里事实上有两种状态 如果从1,n处断开 最大子序列就是[L,R]（L <= R）

然而成环 又会出现[1,R]+[L,n]这样的绕过一圈的情况 事实上也好做 用总和减去1~n链的最小子序列和就好

对于求链的最大子序列和 能够由tr[root].max = max(max(tr[root<<1].max,tr[root<<1|1].max),tr[root>>1].lmax+tr[root>>1|1].rmax) 得出

即为左区间最大子序列和 右区间最大子序列和 左区间右连续的最大子序列和+右区间左连续的最大子序列和 这三个中最大的那个

罪域最小子序列和也是一样 能够由tr[root].min = min(min(tr[root<<1].min,tr[root<<1|1].min),tr[root>>1].lmin+tr[root>>1|1].rmin) 得出

即为左区间最小子序列和 右区间最小子序列和 左区间右连续的最小子序列和+右区间左连续的最小子序列和 这三个中最小的那个

这样答案也非常好得出了 ans = max( tr[1].max,tr[1].sum-tr[1].min );

然而这样会WA 最关键的一点没有注意啊！

。不能够把1~n所有选取 意思也就是说这个最大子序列和不能够是整个环 意思也就是说上面的做法通通WA啊……………………………………………………………………………………………………………………………………………………………………………………

只是莫操心。

。我不是在逗你玩。。。。

(放下板砖 施主听鰯讲。。。

事实上仅仅要统计一下负数的个数即可了 假设存在负数 那就说明最大子序列和肯定不会所有选取 至少扣掉个负数吧 也就是说这样的情况下上面的解答是正确的

可是假设全是正整数 那么就须要扣去一部分 那么扣去哪部分呢 当然是扣去最小子序列和了 事实上说更直白点 就是最小的那个正整数

这样就能够愉快的AC了。。

。

代码例如以下：

#include <iostream>
#include <cmath>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <queue>
#include <stack>
#include <list>
#include <algorithm>
#include <map>
#include <set>
#define LL long long
#define Pr pair<int,int>
#define fread() freopen("in.in","r",stdin)
#define fwrite() freopen("out.out","w",stdout)

using namespace std;
const int INF = 0x3f3f3f3f;
const int msz = 10000;
const int mod = 1e9+7;
const double eps = 1e-8;

struct Tree
{
	int cnt,sum,lmax,rmax,mx,lmin,rmin,mn;
};

Tree tr[400400];
int n;

void init(int root,int l,int r)
{
	if(l == r)
	{
		scanf("%d",&tr[root].sum);
		tr[root].cnt = (tr[root].sum < 0);
		tr[root].lmin = tr[root].rmin = tr[root].mn = tr[root].lmax = tr[root].rmax = tr[root].mx = tr[root].sum;
		return;
	}
	int mid = (l+r)>>1;
	init(root<<1,l,mid);
	init(root<<1|1,mid+1,r);
	tr[root].sum = tr[root<<1].sum+tr[root<<1|1].sum;

	tr[root].lmax = max(tr[root<<1].lmax,tr[root<<1].sum+tr[root<<1|1].lmax);
	tr[root].rmax = max(tr[root<<1|1].rmax,tr[root<<1|1].sum+tr[root<<1].rmax);
	tr[root].mx = max(max(tr[root<<1].mx,tr[root<<1|1].mx),tr[root<<1].rmax + tr[root<<1|1].lmax);

	tr[root].lmin = min(tr[root<<1].lmin,tr[root<<1].sum+tr[root<<1|1].lmin);
	tr[root].rmin = min(tr[root<<1|1].rmin,tr[root<<1|1].sum+tr[root<<1].rmin);
	tr[root].mn = min(min(tr[root<<1].mn,tr[root<<1|1].mn),tr[root<<1].rmin + tr[root<<1|1].lmin);
	tr[root].cnt = tr[root<<1].cnt+tr[root<<1|1].cnt;
}

void Change(int root,int l,int r,int pos,int x)
{
	if(l == r)
	{
		tr[root].lmin = tr[root].rmin = tr[root].mn = tr[root].lmax = tr[root].rmax = tr[root].mx = tr[root].sum = x;
		tr[root].cnt = (x < 0);
		return;
	}
	int mid = (l+r)>>1;

	if(mid >= pos) Change(root<<1,l,mid,pos,x);
	else Change(root<<1|1,mid+1,r,pos,x);

	tr[root].sum = tr[root<<1].sum+tr[root<<1|1].sum;

	tr[root].lmax = max(tr[root<<1].lmax,tr[root<<1].sum+tr[root<<1|1].lmax);
	tr[root].rmax = max(tr[root<<1|1].rmax,tr[root<<1|1].sum+tr[root<<1].rmax);
	tr[root].mx = max(max(tr[root<<1].mx,tr[root<<1|1].mx),tr[root<<1].rmax + tr[root<<1|1].lmax);

	tr[root].lmin = min(tr[root<<1].lmin,tr[root<<1].sum+tr[root<<1|1].lmin);
	tr[root].rmin = min(tr[root<<1|1].rmin,tr[root<<1|1].sum+tr[root<<1].rmin);
	tr[root].mn = min(min(tr[root<<1].mn,tr[root<<1|1].mn),tr[root<<1].rmin + tr[root<<1|1].lmin);
	tr[root].cnt = tr[root<<1].cnt+tr[root<<1|1].cnt;
}

int main()
{
	//fread();
	//fwrite();
	int m,pos,x;

	while(~scanf("%d",&n))
	{
		init(1,1,n);
//		printf("%d\n",tr[1].mx);

		scanf("%d",&m);
		while(m--)
		{
			scanf("%d%d",&pos,&x);
			Change(1,1,n,pos,x);

			if(!tr[0].cnt)
				printf("%d\n",tr[1].sum-tr[1].mn);
			else printf("%d\n",max(tr[1].mx,tr[1].sum-tr[1].mn));
		}

	}

	return 0;
}

id=2750">