KNN算法——分类部分

1.核心思想

如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。也就是说找出一个样本的k个最近邻居，将这些邻居的属性的平均值赋给该样本，就可以得到该样本的属性。

下面看一个例子，

一个程序员面试结束后，想想知道是否拿到offer，他在网上找到几个人的工作经历和大概薪资，如下，X为年龄，Y为工资;

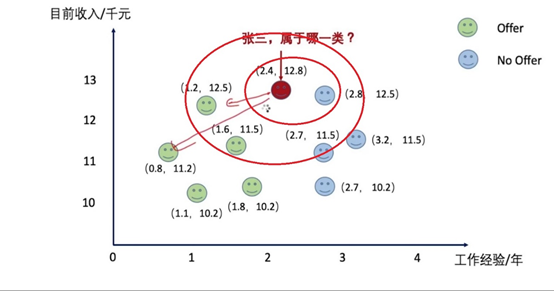
当k取1的时候，我们可以看出距离最近的no offer，因此得到目标点为不被录用。

当k取3的时候，我们可以看出距离最近的三个，分别是有offer 和no offer，根据投票决定 offer的票数较高为2 ，所以被录用。

算法流程

1. 准备数据，对数据进行预处理，常用方法，特征归一化、类别型特征的处理、高维组合特征的处理、组合特征的处理、文本表示模型的模型处理、Word2Vec、图像数据不足时的处理方法

2. 选用合适的数据结构存储训练数据和测试元组，根据模型验证方法，把样本划分不同的训练集和测试集，比如holdout只需要划分为两个部分，交叉验证划分为k个子集，自助法跟着模型来

3. 设定参数，如k的取值，这个涉及到超参数调优的问题，网络搜索、随机搜索、贝叶斯算法等

4.维护一个大小为k的的按距离由大到小的优先级队列，用于存储最近邻训练元组。随机从训练元组中选取k个元组作为初始的最近邻元组，分别计算测试元组到这k个元组的距离，将训练元组标号和距离存入优先级队列

5. 遍历训练元组集，计算当前训练元组与测试元组的距离，将所得距离L 与优先级队列中的最大距离Lmax

6. 进行比较。若L>=Lmax，则舍弃该元组，遍历下一个元组。若L < Lmax，删除优先级队列中最大距离的元组，将当前训练元组存入优先级队列。

7. 遍历完毕，计算优先级队列中k 个元组的多数类，并将其作为测试元组的类别。

8. 测试元组集测试完毕后计算误差率，继续设定不同的k值重新进行训练，最后取误差率最小的k 值。

简单来说，knn算法最重要的是三个要素：K值选择,距离度量,分类决策规则，

K的选择

如k的取值，这个涉及到超参数调优的问题，k的取值对结果会有很大的影响。K值设置过小会降低分类精度，增加模型复杂度；若设置过大，且测试样本属于训练集中包含数据较少的类，则会增加噪声，降低分类效果。通常，K值的设定采用交叉检验的方式（以K=1，K=2，K=3依次进行），K折交叉验证如下：

1）  将全部训练集S分成K个不相交的子集，假设S中的训练样例个数为m，那么每一个子集有m/k个训练样例。

（2）  每次从分好的子集中，选出一个作为测试集，另外k-1个作为训练集。

（3）  根据训练集得到模型。

（4）  根据模型对测试集进行测试，得到分类率。

（5）  计算k次求得的分类率的平均值，作为模型的最终分类率。

以五折交叉验证为例;

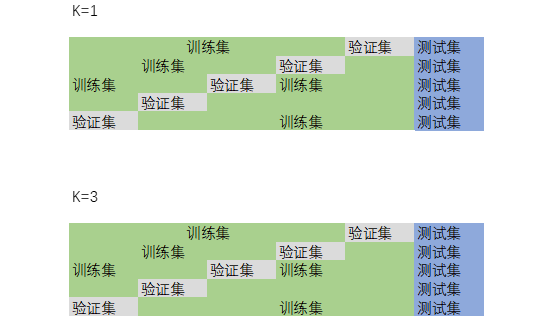
分别得出K=1时的平均分类准确度、K=1时的平均分类准确度……选出最优K值

距离度量

在KNN算法中，常用的距离有三种，分别为曼哈顿距离、欧式距离和闵可夫斯基距离。

距离通式：

当p=1时，称为曼哈顿距离

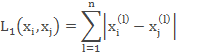
当p=2时，称为欧式距离

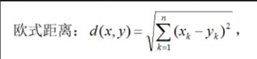
当p=∞时，

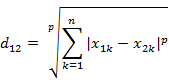
分类决策规则

：

1.多数表决：少数服从多数，即训练集里和预测的样本特征最近的K个样本，预测为里面有最多类别数的类别

2.加权表决：根据各个邻居与测试对象距离的远近来分配相应的投票权重。最简单的就是取两者距离之间的倒数，距离越小，越相似，权重越大，将权重累加，最后选择累加值最高类别属性作为该待测样本点的类别，类似大众评审和专家评审。

这两种确简单直接，在样本量少，样本特征少的时候有效，只适合数据量小的情况。因为我们经常碰到样本的特征数有上千以上，样本量有几十万以上，如果我们这要去预测少量的测试集样本，算法的时间效率很成问题。因此，这个方法我们一般称之为蛮力实现。比较适合于少量样本的简单模型的时候用。一个是KD树实现，一个是球树实现。