HDU4625 JZPTREE——第二类斯特林数

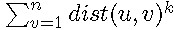
复杂度大概O(nk)

一些尝试：
1.对每个点推出1,2,3，，，到k次方的值。但是临项递推二项式展开也要考虑到具体每个点的dist

2.相邻k次方递推呢？递推还是不能避免k次方的展开

k次方比较讨厌，于是考虑用斯特林数处理

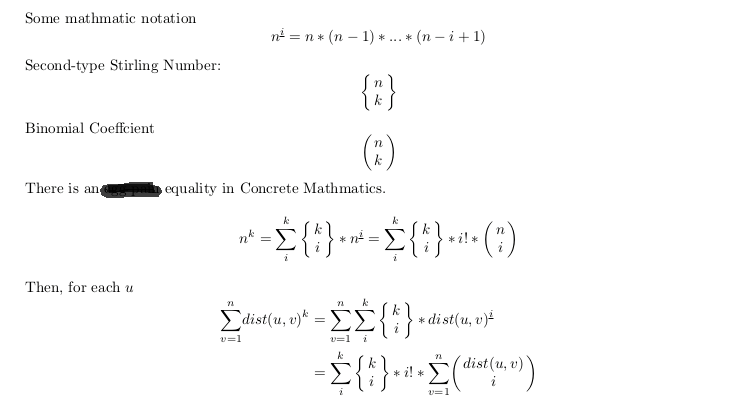
转化成求k个后面这个C(dis,i)

组合数相比较于k次方有什么好处呢？
有直接的简单的递推式！

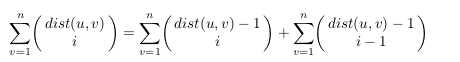
并且恰好的是，可以直接树形dp，距离对于子树恰好-1

O(nk)树形dp一遍

然后换根O(nk)再处理一遍

回到主函数，把之前的那些东西在分别乘上加起来即可。

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=+;
const int K=;
const int mod=;
int n,k,t;
struct node{
    int nxt,to;
}e[*N];
int hd[N],cnt;
int f[N][K];
int g[N][K];
int jie[K],s[K][K];
void add(int x,int y){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;
    hd[x]=cnt;
}
void dfs(int x,int fa){
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa) continue;
        dfs(y,x);
        for(reg j=;j<=k;++j){
            if(j)f[x][j]=(f[x][j]+f[y][j]+f[y][j-])%mod;
            else f[x][j]=(f[x][j]+f[y][j])%mod;
        }
    }
    f[x][]=(f[x][]+)%mod;
}
void sol(int x,int fa){
    if(x==){
        for(reg j=;j<=k;++j) g[x][j]=f[x][j];
    }
    else{
        for(reg j=;j<=k;++j){
            if(j>) g[x][j]=(f[x][j]+(g[fa][j]-(f[x][j]+f[x][j-])+mod)%mod+(g[fa][j-]-(f[x][j-]+f[x][j-]))%mod+mod+mod)%mod;
            else if(j==) g[x][j]=(f[x][j]+(g[fa][j]-(f[x][j]+f[x][j-])+mod)%mod+(g[fa][j-]-(f[x][j-]))%mod+mod+mod)%mod;
            else g[x][j]=n;
        }
    }
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa) continue;
        sol(y,x);
    }
}
void clear(){
    cnt=;
    memset(hd,,sizeof hd);
    memset(f,,sizeof f);
    memset(g,,sizeof g);
}
int main(){
    rd(t);
    s[][]=;
    for(reg i=;i<=;++i){
        for(reg j=;j<=;++j){
            s[i][j]=(s[i-][j-]+j*(s[i-][j])%mod)%mod;
        }
    }
    jie[]=;
    for(reg i=;i<=;++i) jie[i]=jie[i-]*i%mod;
    while(t--){
        clear();
        rd(n);rd(k);
        int x,y;
        for(reg i=;i<n;++i){
            rd(x);rd(y);
            add(x,y);add(y,x);
        }
        dfs(,);
//        for(reg i=1;i<=n;++i){
//            cout<<" ii "<<i<<endl;
//            for(reg j=0;j<=k;++j){
//                cout<<" f[i]["<<j<<"]"<<" : "<<f[i][j]<<endl;
//            }cout<<endl;
//        }cout<<endl;
        sol(,);
//        for(reg i=1;i<=n;++i){
//            cout<<" ii "<<i<<endl;
//            for(reg j=0;j<=k;++j){
//                cout<<" g[i]["<<j<<"]"<<" : "<<g[i][j]<<endl;
//            }cout<<endl;
//        }cout<<endl;

        for(reg i=;i<=n;++i){
            int ans=;
            for(reg j=;j<=k;++j){
                ans=(ans+jie[j]*s[k][j]%mod*g[i][j]%mod)%mod;
            }
            printf("%d\n",ans);
        }
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2018/12/29 19:09:56
*/

总结：
这个就真的比较有趣了

把n^k换成斯特林数，还有一个原因是n^k实在不好支持递推

组合数就比较轻松了。

恰好树形dp的递推特点和组合数的递推式又比较好的吻合在一起！

（当然，n的i次下降幂也有不错的递推性质，也可以不用转化成组合数直接类比递推，本质相同。）