[POJ 3735] Training little cats (结构矩阵、矩阵高速功率）

Training little cats

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 9613		Accepted: 2296

Description

Facer's pet cat just gave birth to a brood of little cats. Having considered the health of those lovely cats, Facer decides to make the cats to do some exercises. Facer has well designed a set of moves for his cats. He is now asking you to supervise the
cats to do his exercises. Facer's great exercise for cats contains three different moves:

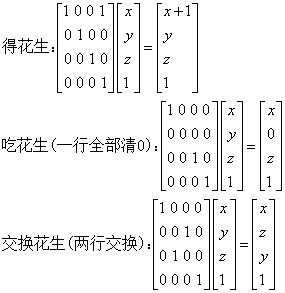
g i : Let the ith cat take a peanut.

e i : Let the ith cat eat all peanuts it have.

s i j : Let the ith cat and jth cat exchange their peanuts.

All the cats perform a sequence of these moves and must repeat it m times! Poor cats! Only Facer can come up with such embarrassing idea. 

You have to determine the final number of peanuts each cat have, and directly give them the exact quantity in order to save them.

Input

The input file consists of multiple test cases, ending with three zeroes "0 0 0". For each test case, three integers n, m and k are given firstly, where n is the number of cats and k is the length of the move
sequence. The following k lines describe the sequence.

(m≤1,000,000,000, n≤100, k≤100)

Output

For each test case, output n numbers in a single line, representing the numbers of peanuts the cats have.

Sample Input

3 1 6
g 1
g 2
g 2
s 1 2
g 3
e 2
0 0 0

Sample Output

2 0 1

Source

PKU Campus 2009 (POJ Monthly Contest – 2009.05.17), Facer

题目大意：

有N仅仅猫，K次操作（得花生、吃花生、交换花生），反复M次。

问最后每仅仅猫各有多少花生剩余。

解题思路：

这道题目的巧妙之处就是构造单位矩阵。从而实现三种操作。

之后便能用矩阵高速幂了。

另外还有两个trick。

1. 由于矩阵的乘法是O（N^3）。复杂度高。这道题直接搞会Ｔ。而我们能够发现，矩阵乘法都是稀疏矩阵，稀疏矩阵乘法有优化。

/*
    稀疏矩阵乘法优化
*/
for (int i = 0; i < n; i++)
    for (int j = 0; j < m; j++) {
        if (!a[i][j]) continue;  //稀疏矩阵乘法优化
        for (int k = 0; k < b.m; k++)
            tmp.a[i][k] += a[i][j] * b.a[j][k];
    }

2. 尽管M，N，K都是 int 范围的，可是操作之后，每仅仅猫的花生数量会超 int。

代码：

/*
ID: wuqi9395@126.com
PROG:
LANG: C++
*/
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<cmath>
#include<cstdio>
#include<vector>
#include<string>
#include<fstream>
#include<cstring>
#include<ctype.h>
#include<iostream>
#include<algorithm>
#define INF (1<<30)
#define PI acos(-1.0)
#define mem(a, b) memset(a, b, sizeof(a))
#define For(i, n) for (int i = 0; i < n; i++)
typedef long long ll;
using namespace std;
const int maxn = 110;
const int maxm = 110;
const int mod = 10000;
struct Matrix {
    int n, m;
    ll a[maxn][maxm];
    void clear() {
        n = m = 0;
        memset(a, 0, sizeof(a));
    }
    Matrix operator * (const Matrix &b) const {
        Matrix tmp;
        tmp.clear();
        tmp.n = n; tmp.m = b.m;
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++) {
                if (!a[i][j]) continue;  //稀疏矩阵乘法优化
                for (int k = 0; k < b.m; k++)
                    tmp.a[i][k] += a[i][j] * b.a[j][k];
            }
        return tmp;
    }
};
int n, k, m;
void init(int n, Matrix &I) {
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j <= n; j++) {
            I.a[i][j] = 0LL;
        }
        I.a[i][i] = 1LL;
    }
    I.n = I.m = n + 1;
 
}
Matrix Matrix_pow(Matrix A, int k) {
    Matrix res;
    init(n, res);
    while(k) {
        if (k & 1) res = res * A;
        k >>= 1;
        A = A * A;
    }
    return res;
}
int main () {
    Matrix A, I, res;
    while(scanf("%d%d%d", &n, &m, &k)) {
        if (m == 0 && n == 0 && k == 0) {
            break;
        }
        A.clear();
        A.n = n + 1; A.m = 1;
        A.a[n][0] = 1LL;
        char ch;
        int u, v;
        init(n, res);
        while(k--) {
            init(n, I);
            getchar();
            scanf("%c", &ch);
            if (ch == 'g') {
                scanf("%d", &u);
                I.a[u - 1][n] = 1LL;
            }
            if (ch == 's') {
                scanf("%d%d", &u, &v);
                I.a[u - 1][u - 1] = 0LL; I.a[u - 1][v - 1] = 1LL;
                I.a[v - 1][v - 1] = 0LL; I.a[v - 1][u - 1] = 1LL;
            }
            if (ch == 'e') {
                scanf("%d", &u);
                I.a[u - 1][u - 1] = 0LL;
            }
            res = I * res;  //每次操作时。I应该乘在前面，由于矩阵乘法没有交换律
        }
        Matrix tmp = Matrix_pow(res, m);
        tmp = tmp * A;
        for (int i = 0; i < n; i++) {
            printf("%lld ", tmp.a[i][0]);
        }
        cout<<endl;
    }
    return 0;
}

上述图片来自：http://blog.csdn.net/magicnumber/article/details/6217602

版权声明：本文博主原创文章，博客，未经同意不得转载。