dfs序+RMQ求LCA详解

首先安利自己倍增求LCA的博客，前置（算不上）知识在此。

LCA有3种求法：倍增求lca（上面qwq），树链剖分求lca（什么时候会了树链剖分再说。），还有，标题。

是的你也来和我一起学习这个了qwq。

开始吧。

众所周知，每当你dfs时，你都能产生一棵dfs树，可以根据你的dfs序来构建。

such as（丑陋的画风）：

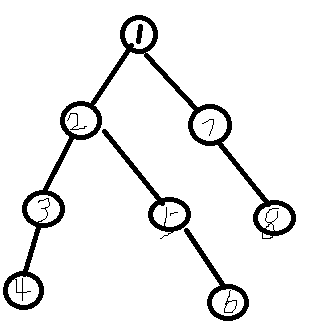
一个dfs的顺序。

以这个为例：

那么我们写出他的遍历顺序：

假如我们要求3,8（wtf？）的LCA，

那么我们首先写出他的bfs序：

123432565217871。

然后留意一下我们要求的两个数的位置。

123432565217871。

我们发现这样一个事情：

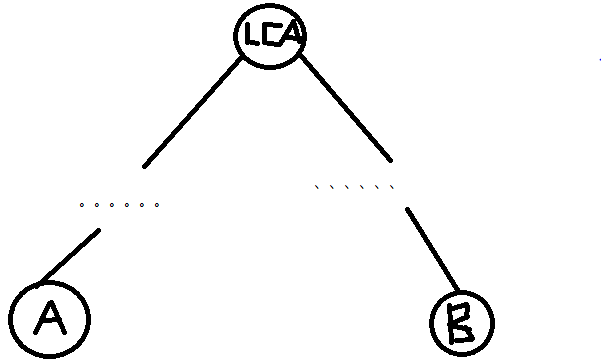
两个数的LCA，一定在前一个数最后一次出现的位置（在bfs序中）。

感性证明：

对于前一个数最后一次出现的位置，他的意义就是当前节点的子树已经遍历完了，并且正在进行回溯！（拍桌，划重点！）。

也就是说，他要回溯到他的祖先了，而它的祖先同样也是后一个节点的祖先，一定在后一个节点遍历前，前一个节点回溯后。

前一个节点<lca<后一个节点。

证毕。

那么，我们只要找到dfs遍历顺序中的 “前一个数最后一次出现的位置，后一个数第一次出现的位置”，这个区间取出区间最小值，即是两个节点的lca。

或许有人会说:为什么最小值一定是lca呢？

又需要证明了。

我们从几何学的角度来解释：

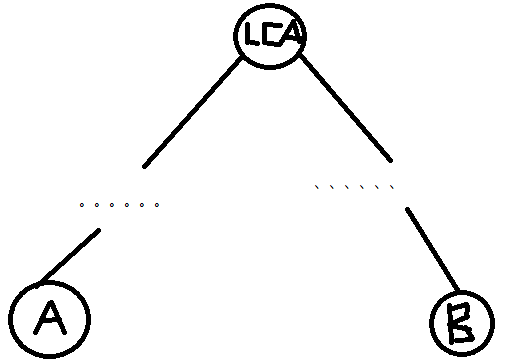
由图可知，两个节点分别在LCA的两个不同的子树中。

当A节点最后一次遍历完，经过一系列回溯，一定能回溯的LCA。

但是因为LCA的子树没有遍历完（链式存图i=edge[i].to），所以它只会遍历到LCA，然后继续遍历lca的子树直到遍历到B点。

感性证毕。

内么，区间最小值且不带修改的我们很容易想到st表。

所以，dfs序+RMQ求LCA成立。

复杂度nlogn查询+o1查询，三者最优。

代码：

#include<bits/stdc++.h>
using namespace std;
const int M = 1e5 +  ;
vector<int> g[M] ;
int n ;

vector<int> vs ;//dfs order
int tot ;
int orm[M] ;
int id[M] ;
int dep[M] ;

int d[M][] ;//RMQ
void dfs (int o , int u ,int  DEP) {
        int tmp = tot ++ ;
        dep[u] = DEP ;
        id[u] = vs.size () ;
        orm[tmp] = u ;
        vs.push_back (tmp) ;

        for (int i =  ; i < g[u].size () ; i ++) {
                int v = g[u][i] ;
                if (v == o) continue ;
                dfs (u , v , DEP + ) ;
        }
        int len = vs.size () ;
        if (vs[len-] == tmp) vs.push_back (vs[id[o]]) ;
        else vs.push_back (tmp) ;
}

void init_RMQ () {
        for (int i =  ; i < *n- ; i ++) d[i][] = vs[i] ;
        for (int j =  ; ( << j) <= n ; j ++) {
                for (int i =  ; i + ( << j) <= n ; i ++) {
                        d[i][j] = min (d[i][j-] , d[i+(<<(j-))][j-]) ;
                }
        }
}

int RMQ (int l , int r) {
        printf ("l = %d , r = %d\n" , l , r ) ;
        int k =  ;
        while ( (<<(k+)) <= r - l + ) k ++ ;
        int tmp = min (d[l][k] , d[+r-(<<k)][k]) ;
        return orm[tmp] ;
}
void Print () {
        for (int i =  ; i < *n- ; i ++) printf ("%3d " , i ) ; puts ("") ;
        puts ("dfs order:") ;
        for (int i =  ; i < *n- ; i ++) printf ("%3d " , vs[i]) ; puts ("") ;
        puts ("deep:") ;
        for (int i =  ; i < n ; i ++) printf ("%3d " , dep[i]) ; puts ("") ;
        puts ("id :") ;
        for (int i =  ; i < n ; i ++) printf ("%3d " , id[i]) ; puts ("") ;
}

void LCA () {
        dfs (,,) ;
        init_RMQ () ;
        Print () ;
}

int main () {
        cin >> n ;
        for (int i =  ; i < n -  ; i ++) {
               int u , v ;
               cin >> u >> v ;
               g[u].push_back (v) ;
               g[v].push_back (u) ;
        }
        LCA () ;
        int Q ;
        cin >> Q ;
        while (Q --) {
                int u , v ;
                cin >> u >> v ;
                if (id[u] > id[v]) swap (u , v ) ;
                int ans = RMQ (id[u] , id[v]) ;
                printf ("The %d and %d the lastest ans is %d , and they are away from %d\n" , u , v , ans , dep[u]+dep[v]-*dep[ans]) ;
        }
        return  ;
}

——lyfdalao

完结。