CF869C The Intriguing Obsession(组合数学瞎搞，O(n)莫名过)

— This is not playing but duty as allies of justice, Nii-chan!

— Not allies but justice itself, Onii-chan!

With hands joined, go everywhere at a speed faster than our thoughts! This time, the Fire Sisters — Karen and Tsukihi — is heading for somewhere they've never reached — water-surrounded islands!

There are three clusters of islands, conveniently coloured red, blue and purple. The clusters consist of aa , bb and ccdistinct islands respectively.

Bridges have been built between some (possibly all or none) of the islands. A bridge bidirectionally connects two different islands and has length 11 . For any two islands of the same colour, either they shouldn't be reached from each other through bridges, or the shortest distance between them is at least 33 , apparently in order to prevent oddities from spreading quickly inside a cluster.

The Fire Sisters are ready for the unknown, but they'd also like to test your courage. And you're here to figure out the number of different ways to build all bridges under the constraints, and give the answer modulo 998244353998244353. Two ways are considered different if a pair of islands exist, such that there's a bridge between them in one of them, but not in the other.

输入输出格式

输入格式：

The first and only line of input contains three space-separated integers aa , bb and cc ( 1<=a,b,c<=50001<=a,b,c<=5000 ) — the number of islands in the red, blue and purple clusters, respectively.

输出格式：

Output one line containing an integer — the number of different ways to build bridges, modulo 998244353998244353 .

输入输出样例

输入样例#1：复制

1 1 1

输出样例#1：复制

输入样例#2：复制

1 2 2

输出样例#2：复制

输入样例#3：复制

1 3 5

输出样例#3：复制

输入样例#4：复制

6 2 9

输出样例#4：复制

813023575

说明

In the first example, there are 33 bridges that can possibly be built, and no setup of bridges violates the restrictions. Thus the answer is 2^{3}=823=8 .

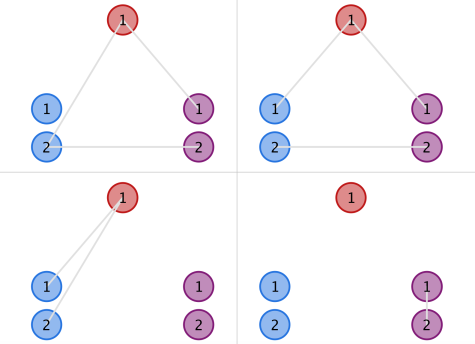
In the second example, the upper two structures in the figure below are instances of valid ones, while the lower two are invalid due to the blue and purple clusters, respectively.

题意：

给出三个区，每个区分别有a,b,c个岛屿，要在区与区之间建设桥梁，但是有如下限制

1：同一个区的两个岛之间不连通或者连通且最短距离不小于3

2：每一座桥的距离假设都为1

问：一共有多少种不同的建桥方法，桥的数量可以是任意的合法的数量。

--translate by 万古神犇517

题解：

哇，这场的背景是物语系列啊~又找到了一场动漫场……

首先来考虑一下哪些情况是会被hack掉的

第一种情况显然是同一个区域里连一条边，这样同一个区域里

所以我们一定每次不能连相同区中的两个点，除此之外还有吗？

显然如果一个点连了另一个区域内的两个点，会让这两个点之间的距离变成2，然后GG

于是我们得出了一个结论

如果在两个区域里连点，两个区域内选的点数一定要相等

即a中选出i个点，必须与b中选出i个点相连

连接种类数为

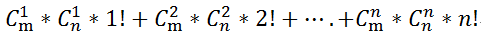
然后我们再来看，如果ab中有两点相连，其中一点再与c相连会出事吗？

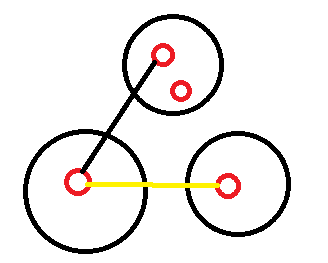
很显然不会对答案产生任何影响

所以我们可以得出另外一个结论

a-b b-c c-a所连的边无论如何都是两两独立的

也就是说，如果a-b连边的可能数为x，b-c连边的可能数为y，c-a连边的可能数为z

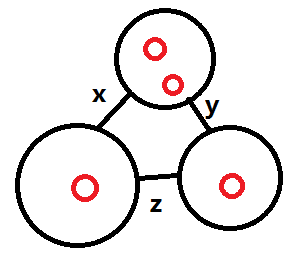
那么既连ab有连bc的可能性是可以直接用乘法原理推得为xy

同理 ab ca为xz,bc ca为yz

所以总答案就是1+x+y+z+xy+yz+xz+xyz

代码如下：

#include<cstdio>

#include<cstring>

#include<iostream>

#include<algorithm>

#define mod 998244353

using namespace std;

long long ans=1ll,fac[],inv[],aa,bb,cc,ab,bc,ca;

long long kasumi(long long a,long long b)

{

    long long ans=;

    while(b)

    {

        if(b&)

        {

            ans=((ans%mod)*a)%mod;

        }

        a=((a%mod)*a)%mod;

        b>>=;

    }

    return ans;

}

long long c(long long n,long long m)

{

    if(n==m)

    {

        return ;

    }

    return (((fac[m]*inv[n])%mod)*inv[m-n])%mod;

}

int main()

{

    fac[]=;

    for(int i=;i<=;i++)

    {

        fac[i]=fac[i-]*i%mod;

    }

    inv[]=kasumi(fac[],mod-);

    for(int i=;i>=;i--)

    {

        inv[i]=inv[i+]*(i+)%mod;

    }

    scanf("%lld%lld%lld",&aa,&bb,&cc);

    for(int i=;i<=min(aa,bb);i++)

    {

        ab+=(((c(i,aa)*c(i,bb))%mod)*fac[i])%mod;

    }

    for(int i=;i<=min(cc,bb);i++)

    {

        bc+=(((c(i,cc)*c(i,bb))%mod)*fac[i])%mod;

    }

    for(int i=;i<=min(aa,cc);i++)

    {

        ca+=(((c(i,aa)*c(i,cc))%mod)*fac[i])%mod;

    }

    ca%=mod;

    bc%=mod;

    ab%=mod;

    ans+=ca+bc+ab;

    ans+=ca*bc;

    ans%=mod;

    ans+=ca*ab;

    ans%=mod;

    ans+=ab*bc;

    ans%=mod;

    ans+=(((ca*bc)%mod)*ab)%mod;

    printf("%lld\n",ans%mod);

}