对numpy.meshgrid()理解

一句话解释numpy.meshgrid()——生成网格点坐标矩阵。
关键词：网格点，坐标矩阵

网格点是什么？坐标矩阵又是什么鬼？
看个图就明白了：

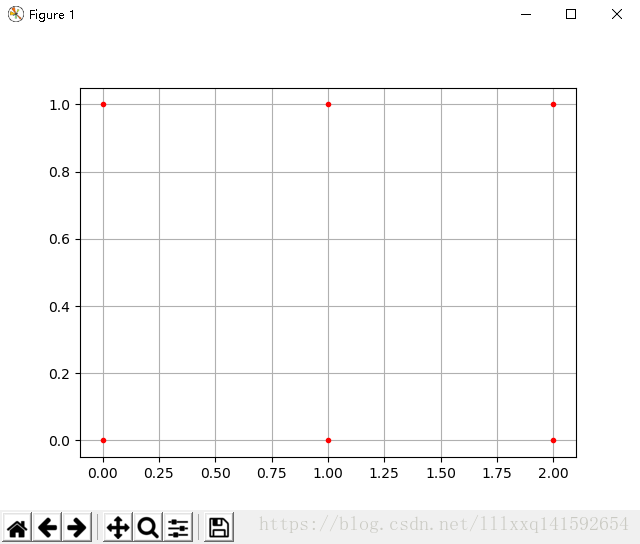
图中，每个交叉点都是网格点，描述这些网格点的坐标的矩阵，就是坐标矩阵。
再看个简单例子

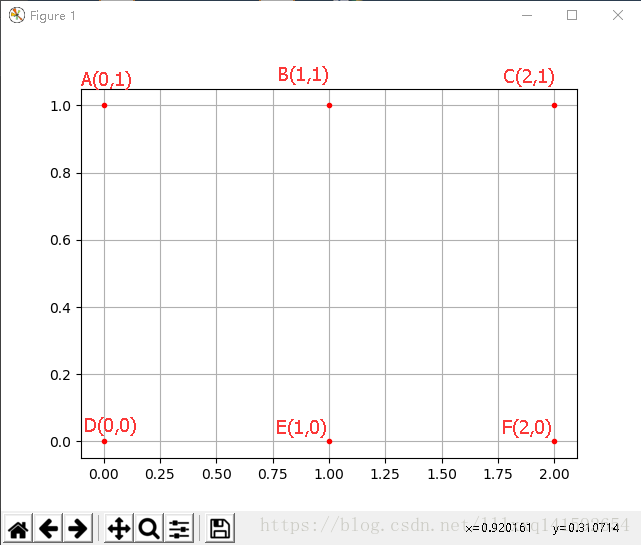
A,B,C,D,E,F是6个网格点，坐标如图，如何用矩阵形式（坐标矩阵）来批量描述这些点的坐标呢？

下面可以自己用matplotlib来试一试，输出就是上边的图

如果对matplotlib不熟悉，可能只知道用一列横坐标（线性代数中的1维列向量），一列纵坐标生成（两者元素个数相等）一些点。但是实际上，给matplotlib的坐标信息是矩阵也是可以的，只要横纵坐标的尺寸一样。都会按照对应关系生成点。

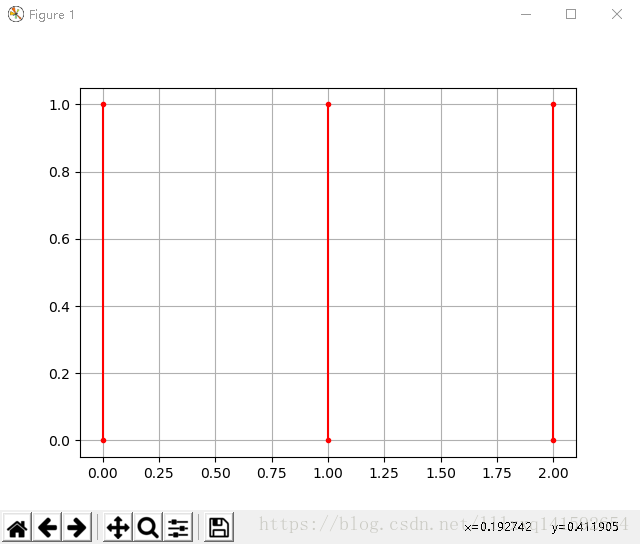
但是有需要注意的地方，按照矩阵给坐标点信息，matplotlib会把横坐标矩阵中，每一列对应的点当做同一条线。
举个例子，把上面的代码plot的linestyle=''删掉，或者变成linestyle='-'（这个操作把图的线型改为默认状态），就会发现A-D是连接的，B-E是连接的，C-F是连接的，也即，会认为你输入的是3条线，如图

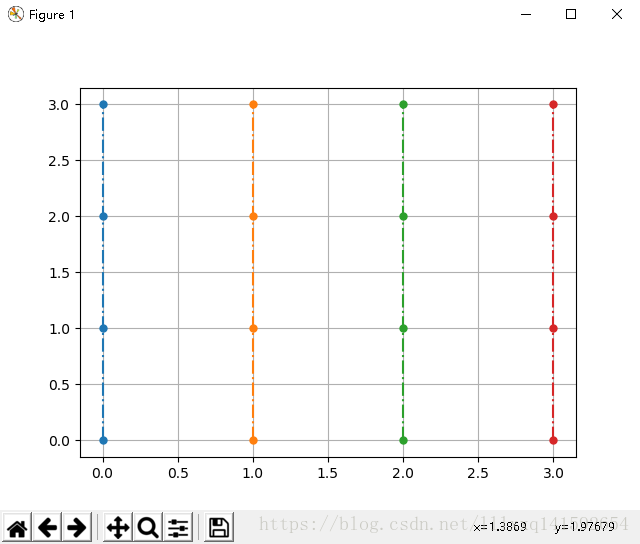
作为练习，自己试着生成如下结果
提示：线型等关键字参数设置可用如下代码

答案

到这里，网格点和坐标矩阵的概念就解释清楚了。

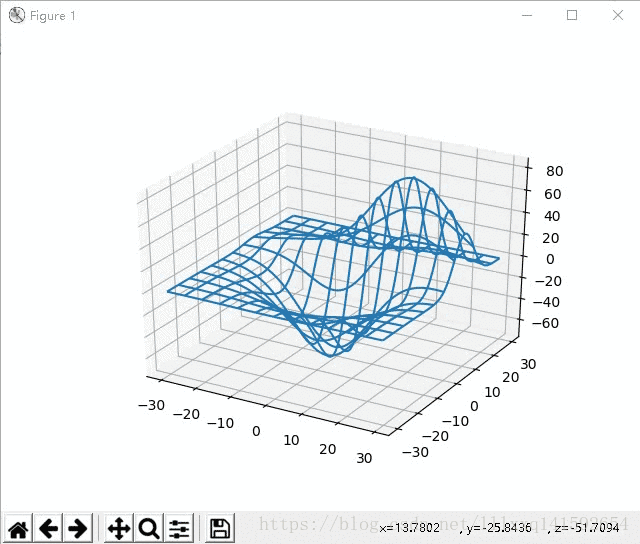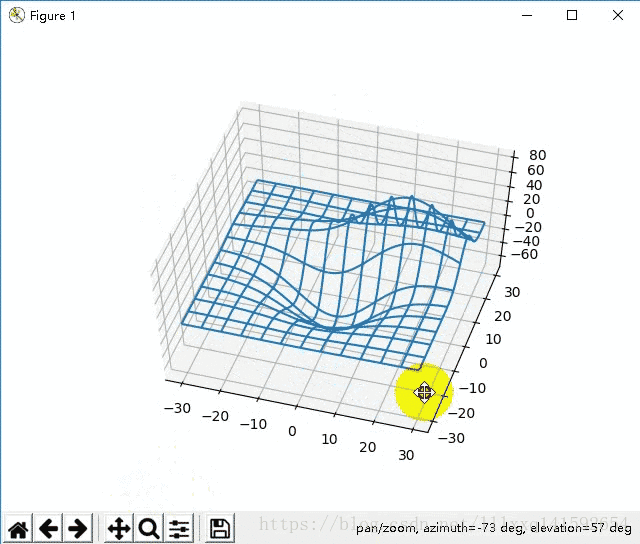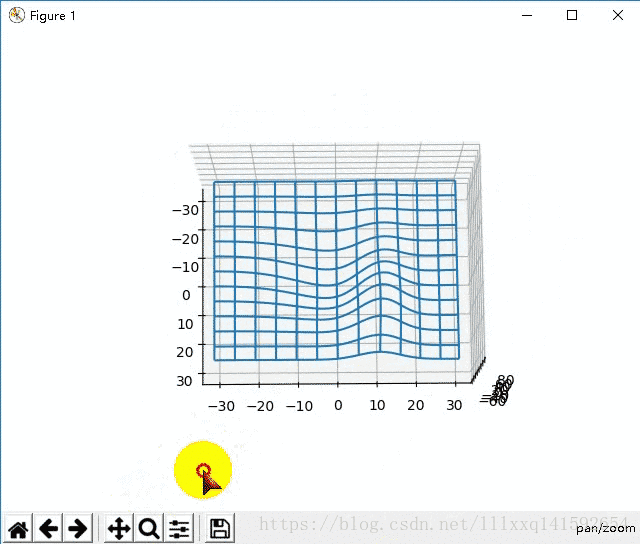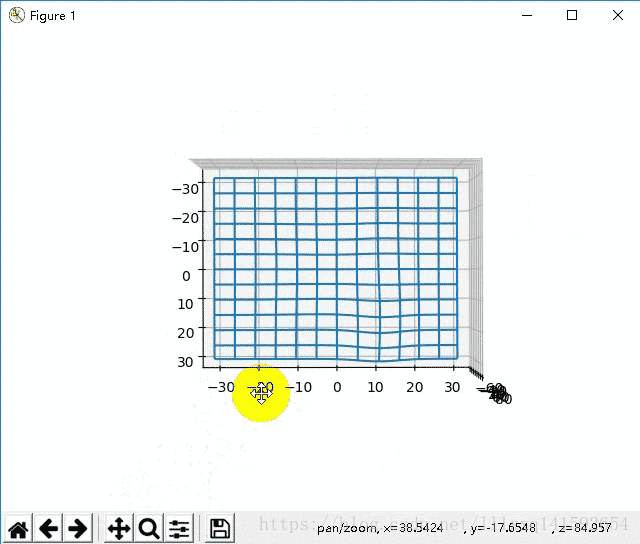
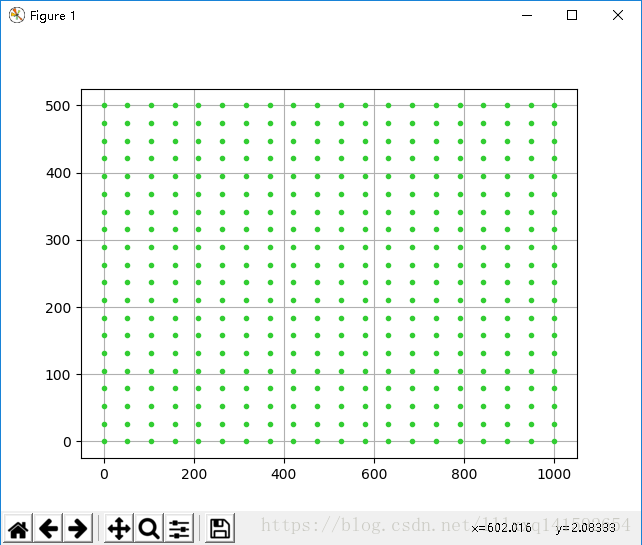
那么问题来了，如果需要的图比较大，需要大量的网格点该怎么办呢？比如下面的这种

最直接但是最笨的方法，就是按照上面的方法把横纵坐标矩阵X XX，Y YY写出来，就像上面练习题中的

很明显，对于网格点很多的情况根本没法用。有啥好的办法吗？
有的，注意到我们练习题中的坐标矩阵，其实有大量的重复——X XX的每一行都一样，Y YY的每一列都一样。基于这种强烈的规律性，numpy提供的numpy.meshgrid()函数可以让我们快速生成坐标矩阵X，Y。

语法：X,Y = numpy.meshgrid(x, y)
输入的x，y，就是网格点的横纵坐标列向量（非矩阵）
输出的X，Y，就是坐标矩阵。

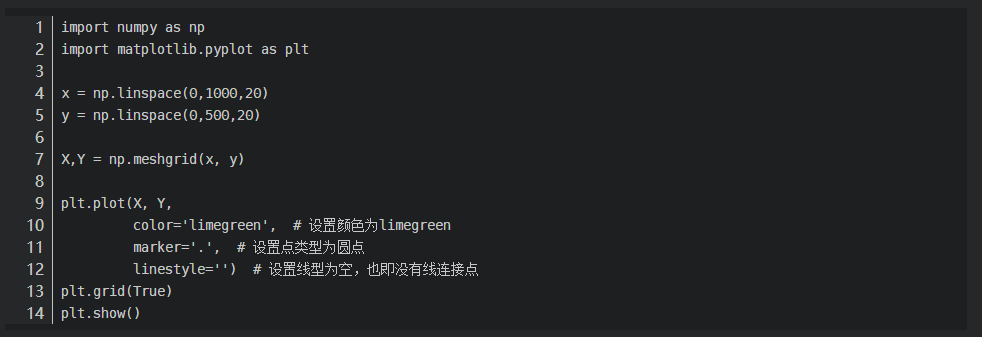
我们来试验一下：改写第一个例子中的代码，用numpy.meshgrid来实现。

最后给出上面这个图的代码

 

————————————————
版权声明：本文为CSDN博主「千千Sama」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/lllxxq141592654/article/details/81532855