Focal and Global Knowledge Distillation for Detectors

一. 概述

论文地址：链接

代码地址：链接

论文简介：

• 此篇论文是在CGNet上增加部分限制loss而来
• 核心部分是将gt框变为mask进行蒸馏

注释：仅为阅读论文和代码，未进行试验，如有漏错请不吝指出。文章的疑惑和假设仅代表个人想法。

二. 详细

2.1 Focal Distillation

2.1.1 mask计算

此篇文章在目标检测蒸馏中对FPN层进行限制，正常的操作如下公式（1）所示：

\[L_{f e a}=\frac{1}{C H W} \sum_{k=1}^{C} \sum_{i=1}^{H} \sum_{j=1}^{W}\left(F_{k, i, j}^{T}-f\left(F_{k, i, j}^{S}\right)\right)^{2}
\]

此篇文章将gt的mask引入到蒸馏中：

如下公式（2），目标为1，背景为0，获得mask矩阵\(M_{i,j}\)

\[M_{i, j}= \begin{cases}1, & \text { if }(i, j) \in r \\ 0, & \text { Otherwise }\end{cases}
\]

但是会出现一个问题，小目标的mask区域太小，比例严重失调会导致小目标的蒸馏效果比较差，解决方法是进行归一化操作，如下公式（3）所示，引用一个尺度（缩放）量\(S_{i,j}\) ， 前景尺度目标大小倒数，目标越大mask越大，但数值越小。背景为mask=0的倒数。也就是每个gt数值和为1，全部背景为1。

疑惑一： 假设前景gt为10，那么前景数值和为10，背景和为1，会不会导致比例失调？

\[\begin{gathered}
S_{i, j}= \begin{cases}\frac{1}{H_{r} W_{r}}, & \text { if }(i, j) \in r \\
\frac{1}{N_{b g}}, & \text { Otherwise }\end{cases} \\
N_{b g}=\sum_{i=1}^{H} \sum_{j=1}^{W}\left(1-M_{i, j}\right)
\end{gathered}
\]

假设一： 假设修改为前景和为1，背景和也为1。前景每个gt数值和相同。如下公式（4）所示，\(N_{gt}\) 为gt的数量

\[\begin{gathered}
S_{i, j}= \begin{cases}\frac{1}{H_{r} W_{r} N_{gt}}, & \text { if }(i, j) \in r \\
\frac{1}{N_{b g}}, & \text { Otherwise }\end{cases} \\
N_{b g}=\sum_{i=1}^{H} \sum_{j=1}^{W}\left(1-M_{i, j}\right)
\end{gathered}
\]

2.1.2 注意力特征计算

这部分参考attention机制，蒸馏也要针对性的对channel和spatial进行学习

以下公式（5）是针对上面两个注意力的计算方式，注意得加绝对值！没有可解释的，就是基础操作。

\[\begin{gathered}
G^{S}(F)=\frac{1}{C} \cdot \sum_{c=1}^{C}\left|F_{c}\right| \\
G^{C}(F)=\frac{1}{H W} \cdot \sum_{i=1}^{H} \sum_{j=1}^{W}\left|F_{i, j}\right|
\end{gathered}
\]

\[\begin{gathered}
A^{S}(F)=H \cdot W \cdot \operatorname{softmax}\left(G^{S}(F) / T\right) \\
A^{C}(F)=C \cdot \operatorname{softmax}\left(G^{C}(F) / T\right)
\end{gathered}
\]

2.1.3 loss融合

直接看下面的公式（7），前景和背景分开进行监督，公式比较简单，\(M_{i,j}\)表示mask，\(S_{i,j}\) 表示mask的尺度，\(A_{i,j}^S/A_k^C\) 表示teacher的注意力特征。

\[\begin{aligned}
&L_{f e a}=\alpha \sum_{k=1}^{C} \sum_{i=1}^{H} \sum_{j=1}^{W} M_{i, j} S_{i, j} A_{i, j}^{S} A_{k}^{C}\left(F_{k, i, j}^{T}-f\left(F_{k, i, j}^{S}\right)\right)^{2} +\beta \sum_{k=1}^{C} \sum_{i=1}^{H} \sum_{j=1}^{W}\left(1-M_{i, j}\right) S_{i, j} A_{i, j}^{S} A_{k}^{C}\left(F_{k, i, j}^{T}-f\left(F_{k, i, j}^{S}\right)\right)^{2}
\end{aligned}
\]

疑惑二： 将上面的公式合并，明显看出 \(\alpha/\beta\) 就表示前景和背景的比例，这明显印证了疑惑一的问题。再从论文图表（7）中调参发现，这两个参数对实际的精度影响不大 \(\pm0.3\) 的精度差异，是否可直接使用假设一的方案，直接去除此两个参数。

由于公式（7）仅对teacher的注意力特征进行了使用，并未对student的注意力特征进行监督，所以引出下面的公式（8）直接监督

\[L_{a t}=\gamma \cdot\left(l\left(A_{t}^{S}, A_{S}^{S}\right)+l\left(A_{t}^{C}, A_{S}^{C}\right)\right)
\]

疑惑三： 为什么公式（7）需要使用teature注意力特征而不使用student的注意力特征？论文没有给出答案，issue上作者也没有给出答案。

假设三：

• 公式（7）中直接去除 \(A_{i,j}^S/A_k^C\) 是否合适？
• 将公式（8）合并到公式（7）中，比如下式的公式（9）所示，当然可以有其他形式

\[L_{f e a}=\alpha \sum_{k=1}^{C} \sum_{i=1}^{H} \sum_{i=1}^{W} M_{i, j} S_{i, j}\left(A_{i, j, t}^{S}-A_{i, j, s}^{S}\right)\left(A_{k, t}^{C}-A_{k, s}^{C}\right)\left(F_{k, i, j}^{T}-f\left(F_{k, i, j}^{S}\right)\right)^{2}+\ldots \ldots
\]

2.2 Global Distillation

此部分来自于CGNet，不做过多介绍，理解较为容易

三. 题外话

3.1 一些可能的笔误

此论文的开源项目基于mmdetection实现，其中试验的YOLOX蒸馏试验有点瑕疵：

• 第一个问题

以下是此论文的项目readme，YOLOX-m的baseline是45.9，但实际YOLOX官方精度是46.9，差一个点已经是非常大了。

作者说用mmdet跑出来YOLOX-m就是这个精度，本人比较怀疑，因为之前跑的YOLOX-S/nano都没问题，YOLOX-m正在试验下周一出结果。

结果： 确实像作者说的达不到官方的精度，本人替换focus到conv，其它未改变，mAP45.2比作者的还低0.7

Student	Teacher	Baseline(mAP)	+FGD(mAP)	config	weight	code
YOLOX-m	YOLOX-l	45.9	46.6	config	baidu	af9g

• 第二个问题

论文中YOLOX-m和repo中的精度不一致，论文45.1，repo是45.9，论文是笔误？

YOLOX-L的精度mmdet已经试验为49.4，为啥这里是48.5？这也是笔误？

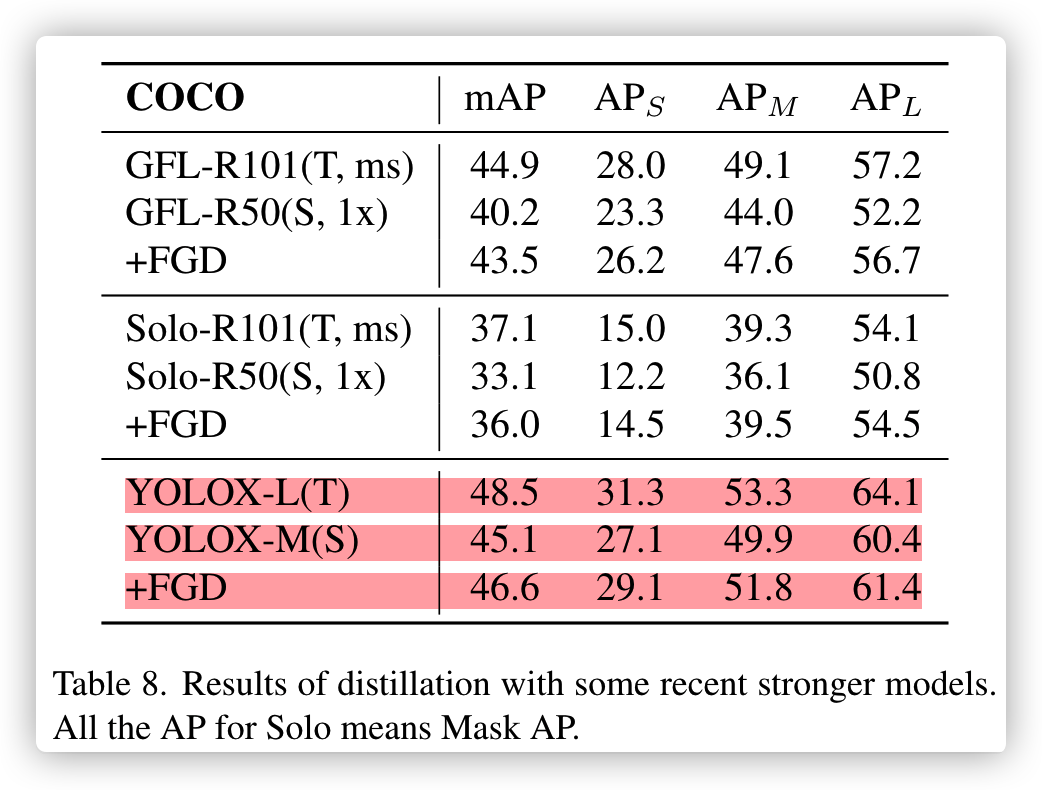
3.2 论文观后感

之前见过类似的做法，用作弱监督中。但未看到将mask用作蒸馏之内，这让我开眼界了。

刚开始看论文的效果确实不错，因为本人对YOLOX较为熟悉，所以仔细看了一下这部分，发现上述问题，作者也没重视。。。

以后实际项目尝试一下，这次仅仅作为阅读论文