算法竞赛进阶指南0x35高斯消元与线性空间

高斯消元

目录

• 高斯消元
  • ACWing207. 球形空间产生器(点击访问)
    • 求解思路
    • 代码
  • ACWing208. 开关问题(点击访问)
    • 思路
    • 代码
    • 总结
    • 欣赏
• 线性空间
  • 定义
  • ACWing209. 装备购买
    • 代码
    • 总结：
  • AcWing210. 异或运算
    • 思路：注意线性空间的推广！
    • DEBUG总结

高斯消元对应的矩阵有两种：

• 常规的线性方程组
• 异或操作（不需要乘上一个数再相减，直接异或即可）
  
  
  
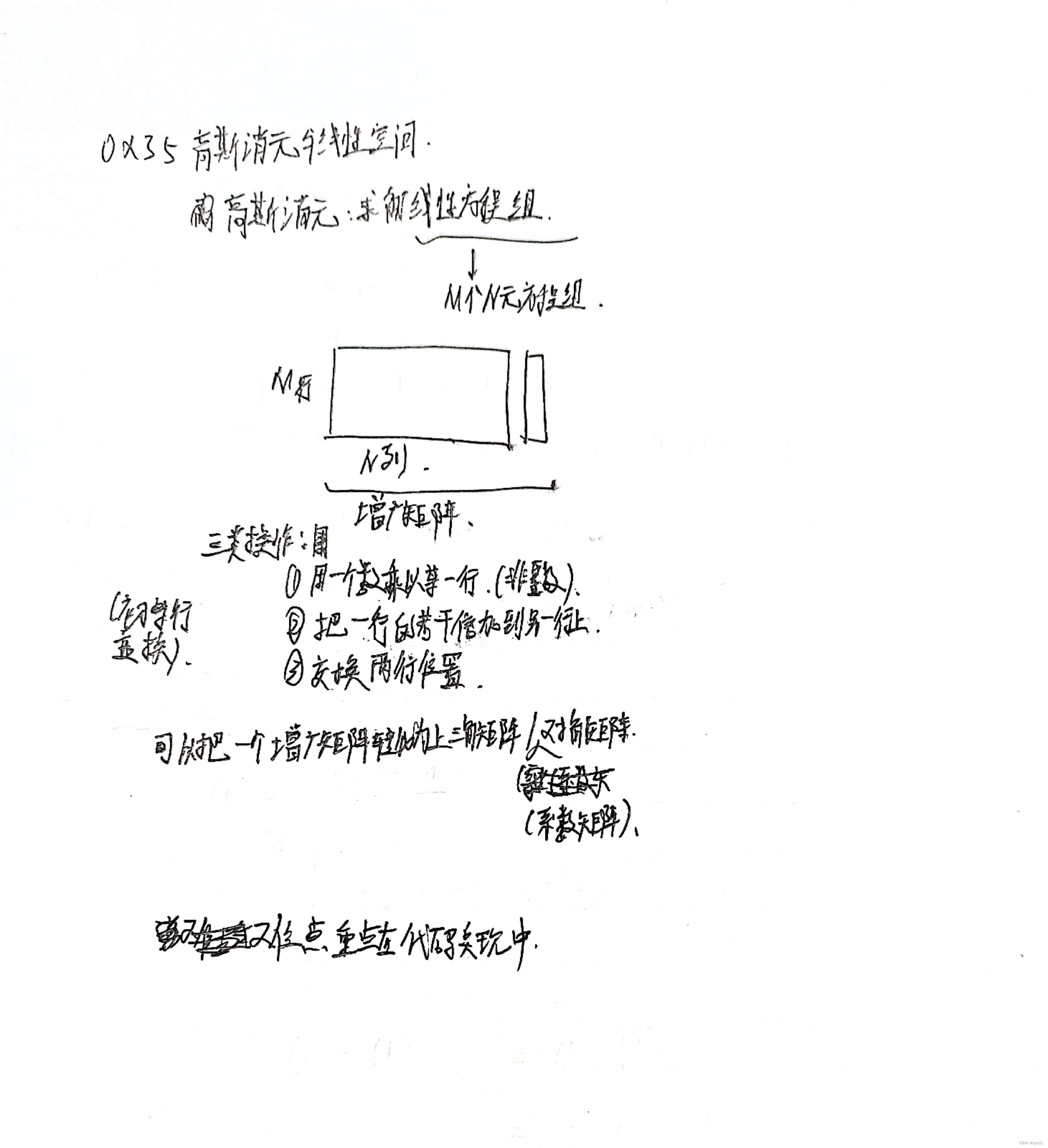
  概念理解起来不太费力，重点是代码实现。

ACWing207. 球形空间产生器(点击访问)

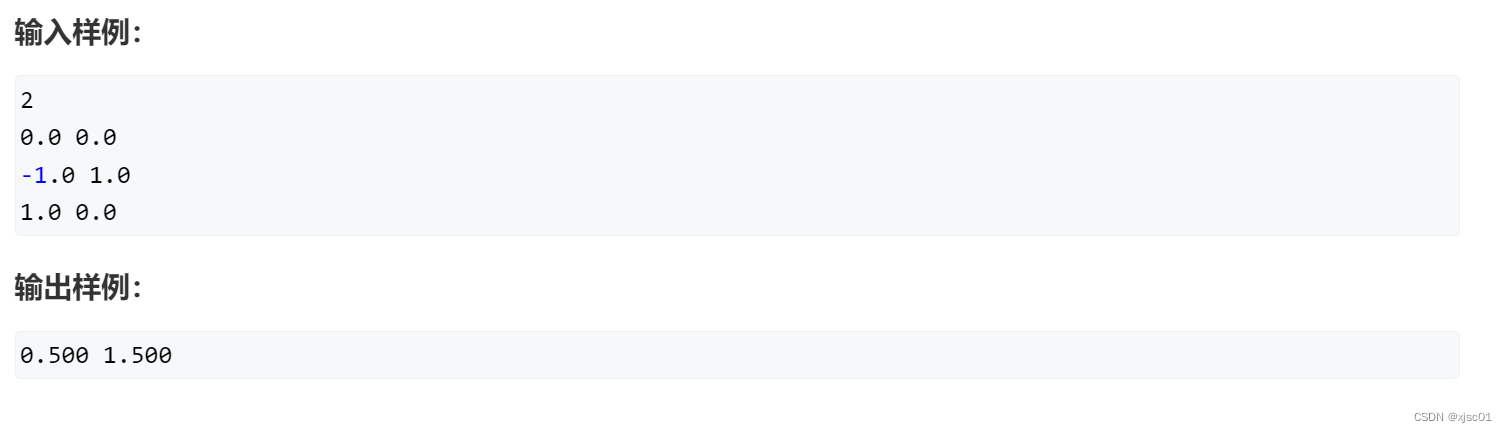
这道题目重点是考察解线性方程组（不太好用暴力来进行解题）

使用解线性方程组来进行求解

求解思路

代码

#include <bits/stdc++.h>
using namespace std;
double a[20][20];
double c[20][20];
double b[20];
const float zero = 1e-8;
int main()
{
    int n;
    //扫描数据
    cin >> n;
    for(int i = 0; i <= n; i++)
        for(int j = 1; j <= n; j++)
            scanf("%lf", &a[i][j]);
    //把其他的与第一个进行相减，然后得到线性增广炬阵（c是系数矩阵，b是增广炬阵）
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= n; j++) c[i][j] = 2 * a[i][j] - 2 * a[0][j];
        for(int j = 1; j <= n; j++) b[i] += a[i][j] * a[i][j] - a[0][j] * a[0][j];
    }
    //进行消元
    for(int i = 1; i  <= n; i++)//第i个变量
    {
        int pos = i;
        while(pos < n && fabs(c[pos][i]) < zero) pos ++;
        for(int j = 1; j <= n; j++) swap(c[pos][j], c[i][j]);
        swap(b[pos], b[i]);
        for(int j = 1; j <= n; j++)
        {
            if(j == pos) continue;
            if(fabs(c[j][i]) > zero)
            {
                double factor = c[j][i] / c[pos][i];
                for(int k = 1; k <= n; k++)
                {
                    c[j][k] -= factor*c[pos][k];
                }
                b[j] -= factor * b[pos];
            }
        }
    }
    for(int i = 1; i <= n; i++)
    {
        double ans = b[i] / c[i][i];
        printf("%.3lf ", ans);
        fflush(stdout);
    }
    return 0;
}

ACWing208. 开关问题(点击访问)

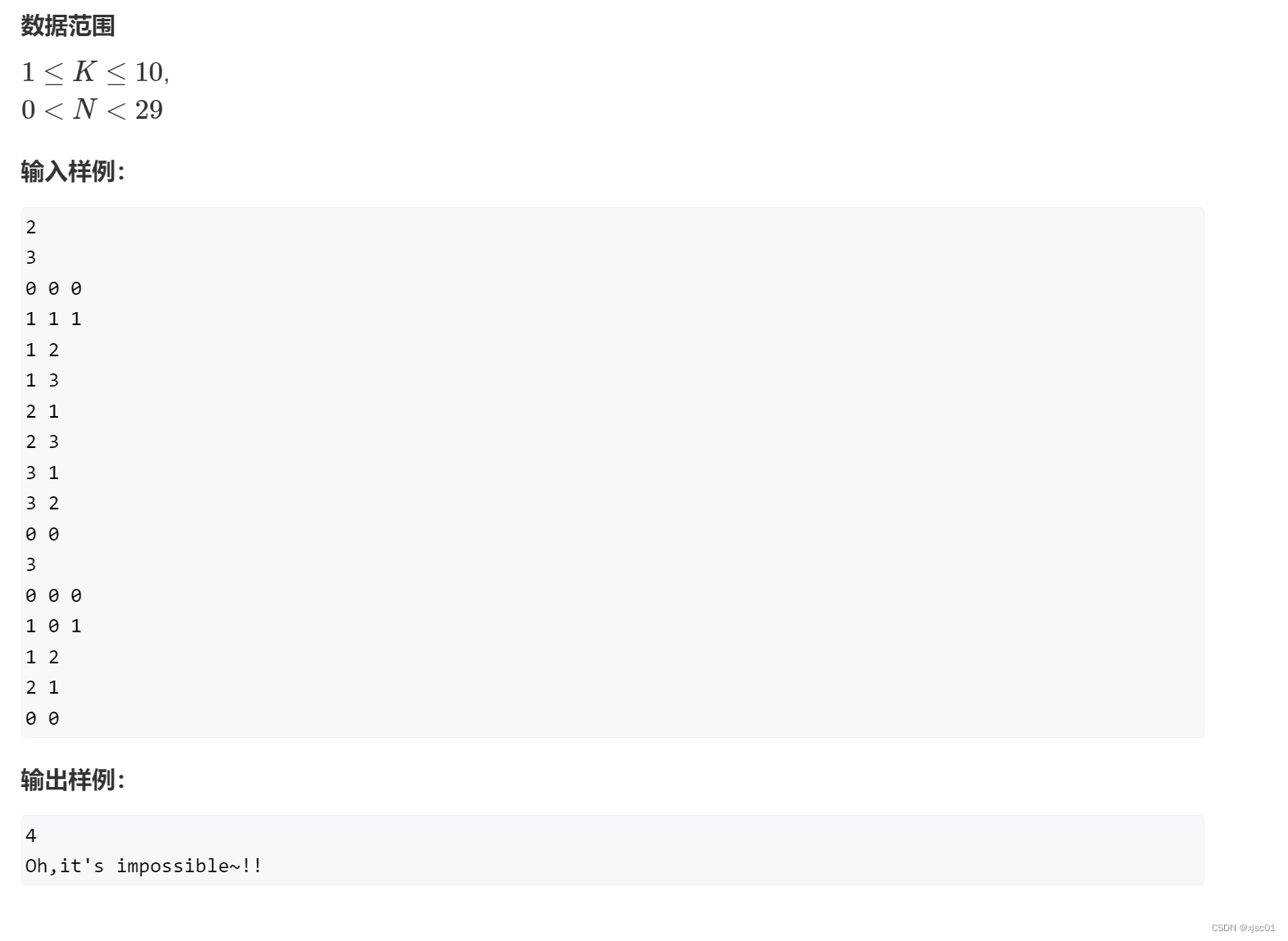
思路

暴力枚举显然是不行。

如果直接取思考解决问题的方法，不太可能。这时候应该与数学相联系。

• 开关的状态只有0，1两种
• 开关打开关闭状态可以用0或者1来进行表示，同时，操作也可以这样。

同时，容易发现：最终操作的结果与按压开关的次序并没有关系。

可以存放一个矩阵

（\(A[i][j]==1，则操作第i个开关会影响第j个开关。特别让A[i][i]==1\)）

根据上面的矩阵，操作某一个开关，这个开关可以看做是一个代号，转化为操作矩阵里面的对应元素。

回顾：（依据矩阵自由元的个数，还可以判断具体有多少种情况）

在矩阵中，如果最终的系数矩阵是单位矩阵，说明有一种情况。

如果有一行系数矩阵全部为0，但是这一行的常数矩阵是1，那么就无解

如果有m行全部都是0，那么就有m个自由变元(最终解的个数就是\(2^m\))

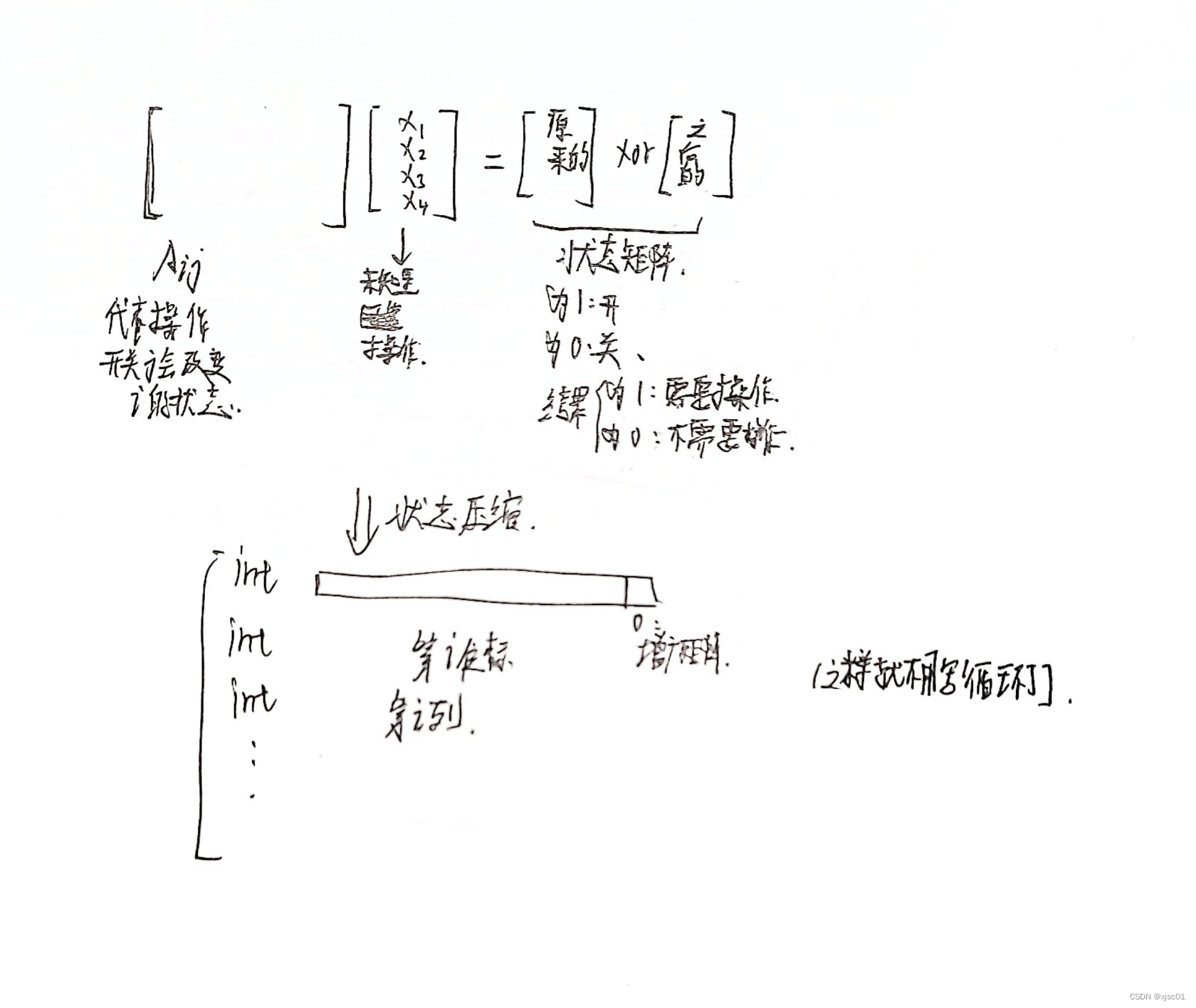
代码

#include <bits/stdc++.h>
using namespace std;
int matrix[40];
void Init()
{
    memset(matrix, 0, sizeof(matrix));
}
inline int col(int x)
{
    return 1 << x;
}
int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        Init();//一定不要忘记初始化
        int cnt = 0;
        bool logical = true;
        int n;
        cin >> n;
        for(int k = 1; k <= 2; k++)
            for(int i = 1; i <= n; i++)
            {
                int tmp = 0;
                scanf("%d", &tmp);
                matrix[i] ^= tmp;
            }
        while(1)
        {
            int x, y;

            scanf("%d%d", &x, &y);
            if(!(x||y)) break;
            matrix[y] = matrix[y] | col(x);
        }
        for(int i = 1; i <= n; i++)
        {
            matrix[i] |= col(i);
        }
        int last = 0;
         for(int i = 1; i <= n; i++)
        {
            int pos = last+1;
            while(pos <= n &&( (matrix[pos]>>i) & 1)==0)
                pos++;
            if(pos > n) continue;
            last = pos;
            swap(matrix[pos], matrix[last]);
            for(int j = 1; j <= n; j++)
            {
                //一定要排除第pos行
                if(j==last) continue;
                if((matrix[j] & col(i)))
                {
                    matrix[j] ^= matrix[last];
                }
            }
        }
        for(int i = 1; i <= n; i++)
        {
            if((matrix[i] >> 1) == 0 && matrix[i] != 0)
            {
                logical = false;
                break;
            }
            if(!matrix[i]) cnt++;
        }

        if(logical)
        {
            if(cnt==0) printf("1\n");
            else{
                int ans = 1 << cnt;
                printf("%d\n", ans);
            }
        }
        else
        {
            printf("Oh,it's impossible~!!\n");
        }
    }
    return 0;
}

总结

答案控制：不需要设置太多的标志，一个ans就够了

if(logical)
        {
            if(cnt==0) printf("1\n");
            else{
                int ans = 1 << cnt;
                printf("%d\n", ans);
            }
        }
        else
        {
            printf("Oh,it's impossible~!!\n");
        }

• 默认ans = 1；
• 如果不可行，就让ans = 0；
• 如果有一个自由元，那么就让ans << 1;

欣赏

int last = 0;//需要给一个last
//以防万一
/*
1 0 0 1
0 0 1 0
0 0 1 0
这种情况
*/
        for(int i = 1; i <= n; i++)//如果行数和列数不相等，还是选取较大的为好
        {
            int pos = last+1;
            while(pos <= n &&( (matrix[pos]>>i) & 1)==0)
                pos++;
            if(pos > n) continue;
            last = pos;
            swap(matrix[pos], matrix[last]);
            for(int j = 1; j <= n; j++)
            {
                //一定要排除第last行
                if(j==last) continue;
                if((matrix[j] & col(i)))
                {
                    matrix[j] ^= matrix[last];
                }
            }
        }

线性空间

定义

线性空间是一个向量集合，并且关于一下两个运算封闭：

1. 向量加法
2. 向量数乘

如果一个向量可以被若干个向量通过向量乘法以及向量加法表示，那么就称这个向量可以被这几个向量线性标出。

线性空间的产生方法：\(a_1,a_2.....a_k\)所能表示的所有向量所构成的集合。

\(a_1,a_2.....a_k\)被称作生成子集。

线性相关&线性无关

任意在向量空间中选出若干个向量，如果某个向量可以被其他向量所表示，那么这些向量线性相关。否则线性无关。

线性空间的基底（基）

• 定义一：线性无关的生成子集；
• 定义二：极大线性无关子集。

线性空间的维数：一个线性空间的所有基包含的向量个数相等，成为维数。

对于一个m行n列的矩阵，如果把每一行看做是长度为m向量（行向量）。这n个向量所能表示的所有向量组成一个线性空间，线性空间的维数就称为矩阵的行秩。同理有列秩。

易知矩阵的行秩等于列秩。统称为秩。

在对一个矩阵进行化简之后，所有的非零行向量就是一个基（初等行变换不改变这些行向量所能表示的线性空间）个数就是矩阵的秩。

---

ACWing209. 装备购买

对于所有装备，把一个装备看成是m维的向量。总体看成是n*m矩阵，然后求出矩阵的基底就行（但是要注意有一个贪心，在每一次选择系数非零的矩阵的时候，应该选择对应的价钱是最小的）

代码

在参考标准代码之后所写的代码：

#include <bits/stdc++.h>
using namespace std;
//注意矩阵运算需要使用double型
#define N 510
long double matrix[N][N];
long double price[N];
const long double eps = 1e-8;
int main()
{
    long double ans = 0;
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            scanf("%Lf", &matrix[i][j]);
    for(int i = 1; i <= n; i++)
        scanf("%Lf", &price[i]);
    int dim = 0;//dim表示基底的数量(和我之前的last相似)
    for(int i = 1; i <= m; i++)
    {
        int now = 0;
        for(int j = dim+1; j<= n; j++)
        {
            if(fabs(matrix[j][i]) > eps && (now==0 || price[j] < price[now]))
                now = j;
        }
        if(now==0)//说明这一个元素是自由元。
            continue;
        dim++;
        ans += price[now];
        for(int j = 1; j <= m; j++)
            swap(matrix[dim][j], matrix[now][j]);
        swap(price[now], price[dim]);
        for(int j = 1; j <= n; j++)
            if(fabs(matrix[j][i]) > eps && j != dim)
            {
                long double rate = matrix[j][i] / matrix[dim][i];
                for(int k = 1; k <= m; k++)
                {
                    matrix[j][k] -= matrix[dim][k] * rate;
                }
            }
    }
    printf("%d %.0Lf", dim, ans);
    return 0;
}

总结：

这道题目失误的地方有两个：

一个是浮点类型的数字在和其他数字进行比较大小的时候，我没有加fabs，导致错误。

还有一点就这道题目卡了double

是在以后所有的数据中，我尽量采用long double来进行运算。

long double的注意事项：

• 输入应该采用%Lf
• 输出应该使用%Lf
• 对应的函数使用fabsl(),cosl()等等。

#include <bits/stdc++.h>
using namespace std;
//注意矩阵运算需要使用double型
#define N 510
long double matrix[N][N];
long double price[N];
const long double eps = 1e-8;
int main()
{
    long double ans = 0;
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            scanf("%Lf", &matrix[i][j]);
    for(int i = 1; i <= n; i++)
        scanf("%Lf", &price[i]);
    int dim = 0;//dim表示基底的数量(和我之前的last相似)
    for(int i = 1; i <= m; i++)
    {
        int now = 0;
        for(int j = dim+1; j<= n; j++)
        {
            if(fabs(matrix[j][i]) > eps && (now==0 || price[j] < price[now]))
                now = j;
        }
        if(now==0)//说明这一个元素是自由元。
            continue;
        dim++;
        ans += price[now];
        for(int j = 1; j <= m; j++)
            swap(matrix[dim][j], matrix[now][j]);
        swap(price[now], price[dim]);
        for(int j = 1; j <= n; j++)
            if(fabs(matrix[j][i]) > eps && j != dim)
            {
                long double rate = matrix[j][i] / matrix[dim][i];
                for(int k = 1; k <= m; k++)
                {
                    matrix[j][k] -= matrix[dim][k] * rate;
                }
            }
    }
    printf("%d %.0Lf", dim, ans);
    return 0;
}

AcWing210. 异或运算

思路：注意线性空间的推广！

异或与线性空间具有一致性

你可以从中选取一些（至少一个）进行异或（xor）运算，从而得到很多不同的结果。

这句话提示了讨论的范围是在把数字当做向量以后所得到的异或空间。

可以通过消元来把复杂的问题变得清晰易懂。

DEBUG总结

1. 对于位运算，判断某一位是不是1的办法
   
   (x>>i)&1
2. 这道题目我万万没有想到：
   
   竟然如果矩阵的秩等于总的行数，那么对于所给的这n个数字，无论如何也整不出一个0来。
   
   但是如果dim小于总的行数，那么这n个向量是线性无关的。所以可以取大于等于1个数字，把他们给消去。

#include <bits/stdc++.h>
using namespace std;
#define N 10010
long long matrix[N];
int main()
{
    int sddsdsafdasg = 1;
    int T;
    cin >> T;
    while(T--)
    {
        printf("Case #%d:\n", sddsdsafdasg++);
        int dim = 0;
        int n, m;
        cin >> n;
        for(int i = 1; i <= n; i++)  scanf("%lld", &matrix[i]);
         /*进行高斯消元*/
        for(int i = 63; i >= 0; i--)
        {
            int now = 0;
            for(int j = dim+1; j <= n; j++)
                if(((matrix[j] >> i) & 1) != 0)
                {
                    now = j;
                    break;
                }
            if(now == 0) continue;
            dim++;
            swap(matrix[dim], matrix[now]);
            for(int j = 1; j<= n; j++)
            {
                if( ((matrix[j]>>i) & 1) == 1 && j!=dim)
                    matrix[j] ^= matrix[dim];
            }

        }
        /*高斯消元完成*/
        scanf("%d", &m);
        for(int t = 1; t <= m; t++)
        {
            int base = 1;
            if(dim >= n) base = 0;
            int cnt = dim;
            long long ans = 0;
            long long  q;
            scanf("%lld", &q);
            q-=base;
            if((unsigned long long)q >= (1LL << dim))
            {
                printf("-1\n");
                continue;
            }
            while(q)
            {
                if(q&1)
                    ans ^= matrix[cnt];
                q >>= 1;
                cnt--;
            }
            printf("%lld\n", ans);
        }
    }
    return 0;
}

---