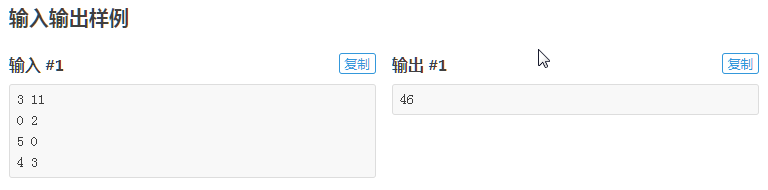
P2212 Watering the Fields S

题目描述

给定n个点，第i个点的坐标为(x_i,y_i)(x_i​,y_i​)，如果想连通第i个点与第j个点，需要耗费的代价为两点的距离。第i个点与第j个点之间的距离使用欧几里得距离进行计算，即：(x_i-x_j)²+(y_i-y_j)²

我们规定耗费代价小于c的两点无法连通，求使得每两点都能连通下的最小代价，如果无法连通输出-1。

输入格式

第一行两个整数n,c代表点数与想要连通代价不能少于的一个数。
接下来n行每行两个整数x_i,y_i描述第i个点。

输出格式

一行一个整数代表使得每两点都能连通下的最小代价，如果无法连通输出 -1。

数据规模

1≤n≤2000，0≤x_i,y_i≤1000，1≤c≤10⁶。

思路：

既然我们想要让这张图中的每两个点之间都能联通，那么这道题很明显就是一道使用最小生成树解决的问题。我们一共有最多2000个点，所以我们可以枚举每两个点之间的距离，然后判断距离是否满足≥c的条件。如果满足，则我们将这条边存储下来。

这里存储边我们仍然使用结构体存储起点、终点和边权的方法。

接下来我们还是要对边依照边权从小到大进行排序。

最后我们只需要跑一遍克鲁斯卡尔算法即可。

完整代码：

 1 #include<iostream>
 2 #include<algorithm>
 3 using namespace std;
 4 int n,c;
 5 struct dian{
 6     int x,y;
 7 }a[2005];
 8 int fa[2005];
 9 struct bian{
10     int start;
11     int end;
12     int dis;
13 }b[4000005];
14 bool cmp(bian a,bian b){
15     return a.dis<b.dis;
16 }
17 int find(int x){
18     if(x==fa[x]){
19         return x;
20     }else{
21         return fa[x]=find(fa[x]);
22     }
23 }
24 void unionn(int x,int y){
25     int r1=find(x);
26     int r2=find(y);
27     fa[r1]=r2;
28 }
29 int main(){
30     cin>>n>>c;
31     for(int i=1;i<=n;i++){
32         cin>>a[i].x>>a[i].y;
33     }
34     int cnt=1;
35     for(int i=1;i<=n;i++){
36         for(int j=i+1;j<=n;j++){
37             if((a[i].x-a[j].x)*(a[i].x-a[j].x)+(a[i].y-a[j].y)*(a[i].y-a[j].y)>=c){
38                 b[cnt].start=i;
39                 b[cnt].end=j;
40                 b[cnt].dis=(a[i].x-a[j].x)*(a[i].x-a[j].x)+(a[i].y-a[j].y)*(a[i].y-a[j].y);
41                 cnt++;
42             }
43         }
44     }
45     cnt--;
46     sort(b+1,b+cnt+1,cmp);
47     for(int i=1;i<=n;i++){
48         fa[i]=i;
49     }
50     int sum=0;//统计加入连通图的点数
51     int ans=0;//统计最小代价
52     for(int i=1;i<=cnt;i++){
53         if(find(b[i].start)!=find(b[i].end)){
54             sum++;
55             ans+=b[i].dis;
56             unionn(b[i].start,b[i].end);
57         }
58         if(sum==n-1){
59             break;
60         }
61     }
62     if(sum<n-1){
63         cout<<-1<<endl;
64     }else{
65         cout<<ans<<endl;
66     }
67     return 0;
68 }

这里要注意一点：两点间的距离在题目的定义中是直接的平方和，所以我们不需要使用double，但同时我们也要注意应当让边权直接与c比较，在比较时也不必对c取平方。