Verilog 加法器和减法器(3)

手工加法运算时候，我们都是从最低位的数字开始，逐位相加，直到最高位。如果第i位产生进位，就把该位作为第i+1位输入。同样的，在逻辑电路中，我们可以把一位全加器串联起来，实现多位加法，比如下面的四位加法电路。这种加法电路叫行波进位加法器。

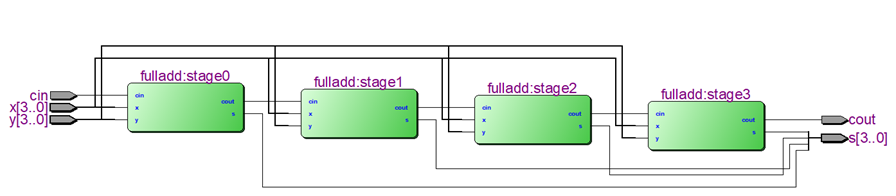
每一级的进位cout传到下一级时都有一个延时，假设为t, 则总的延时为 n*t, n为操作数的位数，比如四位行波进位加法器，为4t。因为t是固定的时间，所以32位或者64位加法时候，这个时延可能不可接受，影响电路的时序，所以我们需要找到更加高效的加法器。

下面是8位行波进位加法器的代码。通过改变参数n的值，我们能够实现的不同位操作数的行波进位加法。

module addern(x, y, s, cout);
  parameter n=8;
  input [n-1:0] x;
  input [n-1:0] y;
  output reg[n-1:0] s;
  output reg cout;
 
  reg [n:0] c;
  integer k;
 
  always @(x,y) begin
    c[0] = 1'b0;
	 for(k = 0; k < n; k = k + 1) begin
	   s[k] = x[k]^y[k]^c[k];
		c[k+1] = (x[k]&y[k])|(x[k]&c[k])|(y[k]&c[k]);
	 end
	 cout = c[n];
 
  end
 
endmodule

或者我们能够使用generate  … endgenerate，在其中用for循环实例化fulladd模块来实现同样功能。代码如下：

module addern(x, y, s, cout);
  parameter n=32;
  input [n-1:0] x;
  input [n-1:0] y;
  output [n-1:0] s;
  output  cout;
 
  wire [n:0] c;
  genvar k;
  assign c[0]=0;
  assign cout=c[n];
 
  generate
	 for(k = 0; k <= n-1; k = k + 1) begin:addbit
       fulladd stage(c[k],x[k],y[k],s[k],c[k+1]);
	 end
  endgenerate
 
endmodule

使用下面的testbench代码:

`timescale 1ns/1ns
`define clock_period 20
 
module addern_tb;
  reg [7:0] x,y;
 
  wire cout;
  wire [7:0] s;
  reg clk;
 
  addern #(.n(8)) addern_0(
						.x(x),
						.y(y),
						.s(s),
						.cout(cout)
                  );
 
  initial clk = 0;
  always #(`clock_period/2) clk = ~clk;
 
  initial begin
     x = 0;
     repeat(20)
	    #(`clock_period) x = $random;
 
  end
 
  initial begin
     y = 0;
     repeat(20)
	    #(`clock_period) y = $random;
 
  end
 
  initial begin
     #(`clock_period*20)
	  $stop;
  end
 
endmodule

进行功能验证，我们得到如下的波形，注意设置radix位unsigned，以便查看结果是否正确。

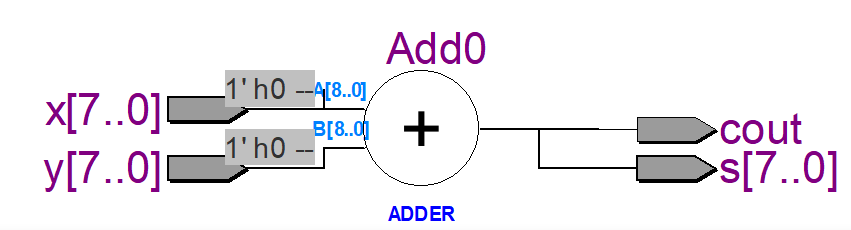
我们也可以使用下面的代码实现相同的功能。这段代码在quartus II选用Cyclone IV E-EP4CE10F17C8综合后，得到下面的逻辑电路，应该是调用了内置的加法器ip。

module addern( x, y,s,cout);
 
  parameter n=8;
  input [n-1:0] x;
  input [n-1:0] y;
  output [n-1:0] s;
  output  cout;
 
  assign {cout, s} = x + y ;
 
endmodule