UVA 10652 Board Wrapping(凸包)

The small sawmill in Mission, British Columbia, has
developed a brand new way of packaging boards for
drying. By fixating the boards in special moulds, the
board can dry efficiently in a drying room.
Space is an issue though. The boards cannot be
too close, because then the drying will be too slow.
On the other hand, one wants to use the drying room
efficiently.
Looking at it from a 2-D perspective, your task is
to calculate the fraction between the space occupied by
the boards to the total space occupied by the mould.
Now, the mould is surrounded by an aluminium frame
of negligible thickness, following the hull of the boards’
corners tightly. The space occupied by the mould
would thus be the interior of the frame.
Input
On the first line of input there is one integer, N ≤ 50,
giving the number of test cases (moulds) in the input. After this line, N test cases follow. Each test case
starts with a line containing one integer n, 1 < n ≤ 600, which is the number of boards in the mould.
Then n lines follow, each with five floating point numbers x, y, w, h, ϕ where 0 ≤ x, y, w, h ≤ 10000
and −90◦ < ϕ ≤ 90◦
. The x and y are the coordinates of the center of the board and w and h are the
width and height of the board, respectively. ϕ is the angle between the height axis of the board to the
y-axis in degrees, positive clockwise. That is, if ϕ = 0, the projection of the board on the x-axis would
be w. Of course, the boards cannot intersect.
Output
For every test case, output one line containing the fraction of the space occupied by the boards to the
total space in percent. Your output should have one decimal digit and be followed by a space and a
percent sign (‘%’).
Note: The Sample Input and Sample Output corresponds to the given picture
Sample Input
1
4
4 7.5 6 3 0
8 11.5 6 3 0
9.5 6 6 3 90
4.5 3 4.4721 2.2361 26.565
Sample Output
64.3 %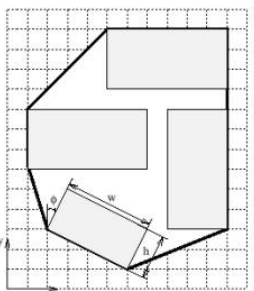

题解：求矩形面积与凸包面积的比例，顺时针一定要是负....错了半天。。。还有给的ang要转化为rad

代码：

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 const double Pi=acos(-1.0);
 struct Point{
     double x,y;
     Point(double x=,double y=):x(x),y(y){}
 };
 typedef Point Vector;
 bool operator < (Point a,Point b){return a.x<b.x||(a.x==b.x&&a.y<b.y);}
 Vector operator - (Point a,Point b){return Vector(a.x-b.x,a.y-b.y);}
 double Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}
 double Length(Vector a){return sqrt(Dot(a,a));}
 double Angle(Vector a,Vector b){return acos(Dot(a,b)/Length(a)/Length(b));}
 Vector Rotate(Vector a,double rad){return Vector(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad));}
 double Cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;}
 Point operator + (Point a,Vector b){return Point(a.x+b.x,a.y+b.y);}
 Point getdot(Point a,Vector b,double ang){return a+Rotate(b,ang);}
 double getrad(double ang){return Pi*(ang/);}
 Point ans[],at[];
 int nu;
 double polygonArea(){
     int k=;
     for(int i=;i<nu;i++){
         while(k>&&Cross(ans[k-]-ans[k-],at[i]-ans[k-])<=)k--;
         ans[k++]=at[i];
     }
     int p=k;
     for(int i=nu-;i>=;i--){
         while(k>p&&Cross(ans[k-]-ans[k-],at[i]-ans[k-])<=)k--;
         ans[k++]=at[i];
     }
     double x=;
     k--;
     if(k<)return ;
     for(int i=;i<k-;i++)x+=Cross(ans[i]-ans[],ans[i+]-ans[]);
     return x/;
 }
 int main(){
     int T,n;
     double x,y,w,h,ang;
     scanf("%d",&T);
     while(T--){
         double area1=,area2=;
         nu=;
         scanf("%d",&n);
         while(n--){
             scanf("%lf%lf%lf%lf%lf",&x,&y,&w,&h,&ang);
             area2+=w*h;
             Point a;
             ang=-getrad(ang);//因为是顺时针旋转的，所以要是负的。。。。。
             at[nu++]=getdot(Point(x,y),Vector(w/,h/),ang);
             at[nu++]=getdot(Point(x,y),Vector(-w/,h/),ang);
             at[nu++]=getdot(Point(x,y),Vector(w/,-h/),ang);
             at[nu++]=getdot(Point(x,y),Vector(-w/,-h/),ang);
         }
         sort(at,at+nu);
         area1=polygonArea();
     //    printf("%lf %lf\n",area1,area2);
         printf("%.1lf %%\n",*area2/area1);
     }
     return ;
 }