Harris Corner（Harris角检测）

在做图像匹配时，常需要对两幅图像中的特征点进行匹配。为了保证匹配的准确性，所选择的特征必须有其独特性，角点可以作为一种不错的特征。

那么为什么角点有其独特性呢？角点往往是两条边缘的交点，它是两条边缘方向变换的一种表示，因此其两个方向的梯度变换通常都比较大并且容易检测到。

这里我们理解一下Harris Corner 一种角点检测的算法

角点检测基本原理：

人们通常通过在一个小的窗口区域内观察点的灰度值大小来识别角点，如果往任何方向移动窗口都会引起比较大的灰度变换那么往往这就是我们要找的角点。如下图右

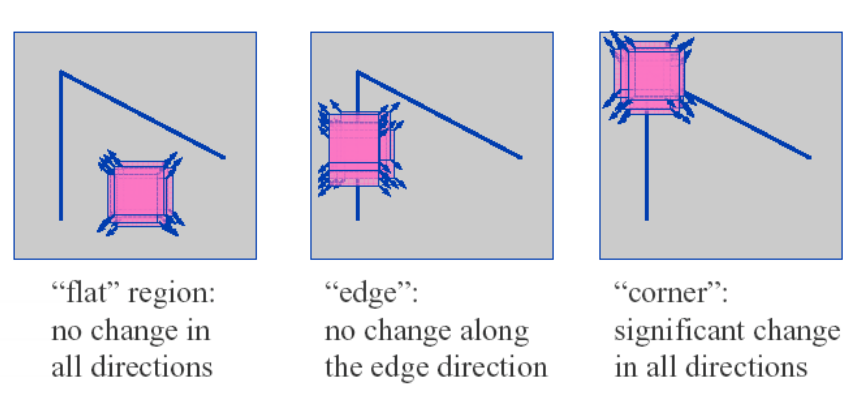
下面我们看一下Harris的数学公式，对于[x,y]平移[u,v]个单位后强度的变换有下式,I(x+u,y+v)是平移后的强度，I(x,y)是原图像像素。对于括号里面的值，如果是强度恒定的区域，那么它就接近于零，反之如果强度变化剧烈那么其值将非常大，所以我们期望E(u,v)很大。

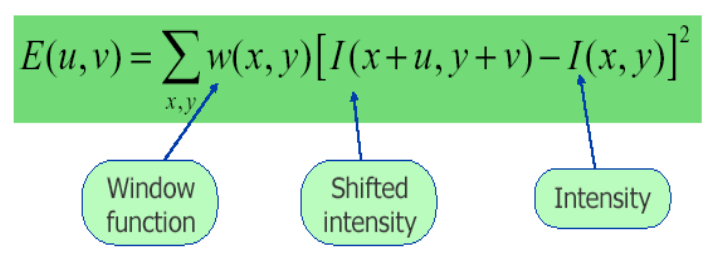
其中w是窗函数，它可以是加权函数，也可以是高斯函数

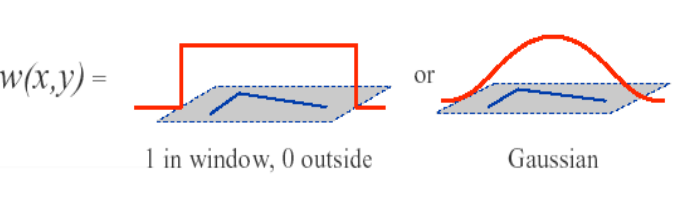
利用二维泰勒展开式我们有

所以其中一阶可以近似为

于是我们可以给出Harris Corner的如下推导，其中Ix，Iy是x，y方向的Gradient模，乘以位移得到位移后的量

对于小的位移，我们可以用双线性插值方法近似：

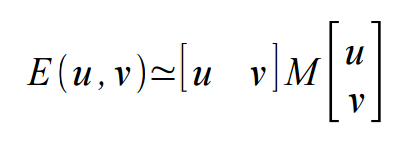
其中M为2*2矩阵如下

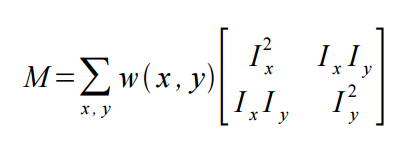
在本质上我们可以把二次项看成一个椭圆函数，我们对M进行特征值分析有λ1，λ2

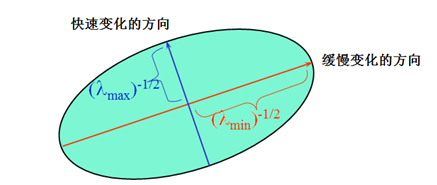
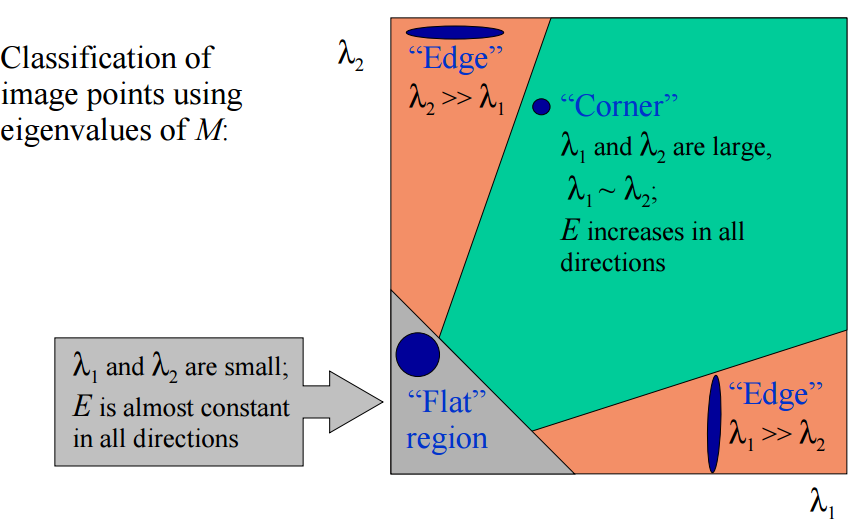
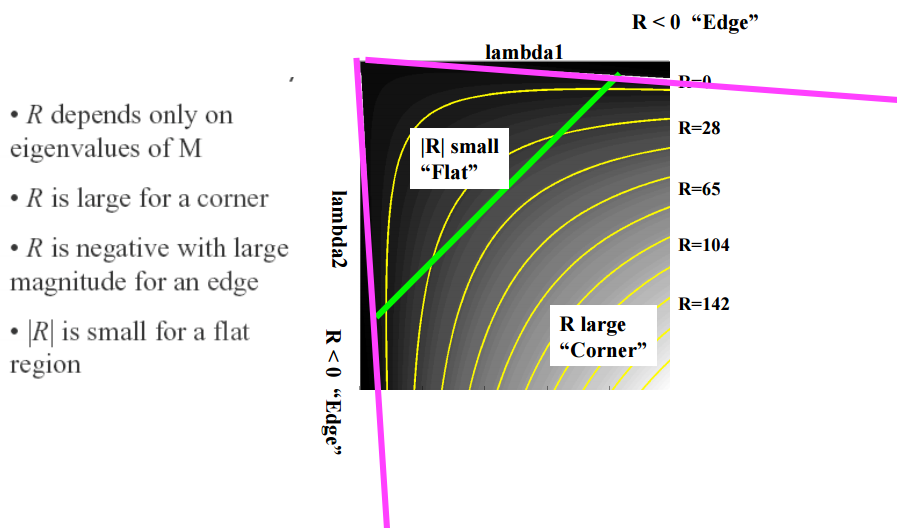
根据λ1，λ2的值我们可以把其分为三类：

1.λ1，λ2都很小且近似，E在所以方向接近于常数；

2.λ1>>λ2,或者λ2>>λ1, E将在某一方向上很大；

3.λ1，λ2都很大且近似，E将在所以方向上很大；

如图所示：

最后我们通过计算角点响应值R来判断其属于哪个区间

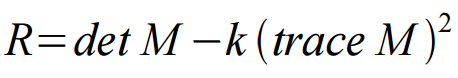
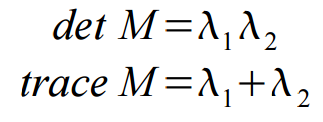
其中k一般为常数取在0.04-0.06间。

算法步骤：

1.计算图像x,y方向的梯度I_x，I_y

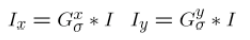
2.计算每个像素点的梯度平方

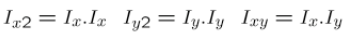
3.计算梯度在每个像素点的和

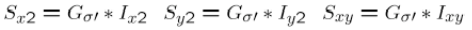
4.定义在每个像素点的矩阵H，也就是前面的M

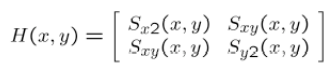
5.计算每个像素的角点响应

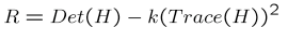
6.设置阈值找出可能点并进行非极大值抑制

代码：

close all
clear all

I = imread('empire.jpg');
I = rgb2gray(I);
I = imresize(I,[500,300]);
imshow(I);

sigma = 1;
halfwid = sigma * 3;

[xx, yy] = meshgrid(-halfwid:halfwid, -halfwid:halfwid);

Gxy = exp(-(xx .^ 2 + yy .^ 2) / (2 * sigma ^ 2));
Gx = xx .* exp(-(xx .^ 2 + yy .^ 2) / (2 * sigma ^ 2));
Gy = yy .* exp(-(xx .^ 2 + yy .^ 2) / (2 * sigma ^ 2));

%%apply sobel in herizontal direction and vertical direction compute the
%%gradient
%fx = [-1 0 1;-1 0 1;-1 0 1];
%fy = [1 1 1;0 0 0;-1 -1 -1];
Ix = conv2(I,Gx,'same');
Iy = conv2(I,Gy,'same');
%%compute Ix2, Iy2,Ixy
Ix2 = Ix.*Ix;
Iy2 = Iy.*Iy;
Ixy = Ix.*Iy;

%%apply gaussian filter
h = fspecial('gaussian',[6,6],1);
Ix2 = conv2(Ix2,h,'same');
Iy2 = conv2(Iy2,h,'same');
Ixy = conv2(Ixy,h,'same');
height = size(I,1);
width = size(I,2);
result = zeros(height,width);
R = zeros(height,width);
Rmax = 0;
%% compute M matrix and corner response
for i = 1:height
    for j =1:width
        M = [Ix2(i,j) Ixy(i,j);Ixy(i,j) Iy(i,j)];
        R(i,j) = det(M) - 0.04*(trace(M)^2);
        if R(i,j)> Rmax
            Rmax = R(i,j);
        end
    end
end
%% compare whith threshold
count = 0;
for i = 2:height-1
    for j = 2:width-1
        if R(i,j) > 0.01*Rmax
            result(i,j) = 1;
            count = count +1;
        end
    end
end

%non-maxima suppression
result = imdilate(result, [1 1 1; 1 0 1; 1 1 1]);

[posc,posr] = find(result == 1);
imshow(I);
hold on;
plot(posr,posc,'r.');

本文原创，转载请注明出处