三维网格补洞算法（Poisson Method）

　　下面介绍一种基于Poisson方程的三角网格补洞方法。该算法首先需要根据孔洞边界生成一个初始化补洞网格，然后通过法向估算和Poisson方程来修正补洞网格中三角面片的几何形状，使其能够适应并与周围的原始网格融合。算法的主要步骤如下：

　　1-检测孔洞边界并初始化补洞网格

　　2-调整补洞网格

　　　　2.1-计算补洞网格中顶点的期望法向

　　　　2.2-基于期望法向旋转补洞网格中的三角面片

　　　　2.3-基于Poisson方程调整补洞网格顶点位置

　　下面分别介绍算法中每一步的具体过程：

1：检测孔洞边界并初始化补洞网格

　　检测孔洞边界和初始化补洞网格方法与以前介绍的方法相同。由于初始化补洞网格无法与原始孔洞周围的网格有效融合，因此需要调整补洞网格的顶点位置使得补洞网格与原始网格之间光滑过渡。

2.1：计算补洞网格中顶点的期望法向

　　由于已知原始网格孔洞边界的法向，将其作为补洞网格边界的法向，构建Laplace方程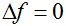求解补洞网格内部顶点的法向分布。

• Laplace算子：

　　假设f表示在每个顶点上的标量，那么网格域上在顶点x_i处的Laplace算子定义如下（不考虑面积影响）：

其中N₁(x_i)表示顶点x_i的1环邻域点，α_ij和β_ij为边e_ij对应的2个对角。

2.2：基于期望法向旋转补洞网格中的三角面片

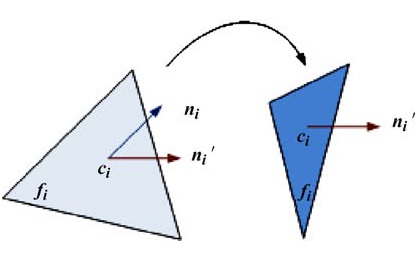
　　计算得到补洞网格中顶点的期望法向之后，可以进一步求得三角面片的期望法向，三角面片的期望法向是其三个顶点期望法向的平均值，然后补洞网格中所有的三角面片根据期望法向进行旋转。旋转参数计算方法如下：假设n_i、n_i’和c_i为三角面片f_i的原始法向、期望法向和重心位置，n_i与n_i’的叉乘方向a为三角面片f_i的旋转轴方向，n_i与n_i’之间的夹角φ为三角面片f_i的旋转角度，那么三角面片f_i将以c_i为旋转中心，绕旋转轴a旋转角度φ到新的位置。

2.3：基于Poisson方程调整补洞网格顶点位置

　　旋转补洞网格的三角面片会撕裂补洞网格，因此我们利用Poisson方程将其重构成连续的网格曲面。在建立Poisson方程时我们需要先计算撕裂网格的梯度场，将其作为Poisson方程的引导场，从而进行网格顶点位置的调整。

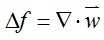
其中f为待求的调整后网格顶点位置，w为撕裂网格的梯度场。

• 梯度算子：

　　假设f表示在每个顶点上的标量，那么网格域上标量场f在任意三角面片T内的梯度算子定义如下：

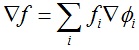
其中基函数梯度▽Φ_i的表达式是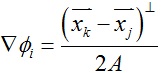，⊥表示将向量逆时针旋转90度，A_T表示三角片T的面积。

• 散度算子：

　　假设w表示在每个三角片上的向量，那么网格域上向量场w在顶点x_i处的散度算子定义如下：

其中T₁(x_i)表示顶点x_i的1环邻域三角片，A_T表示三角片T的面积。

效果：

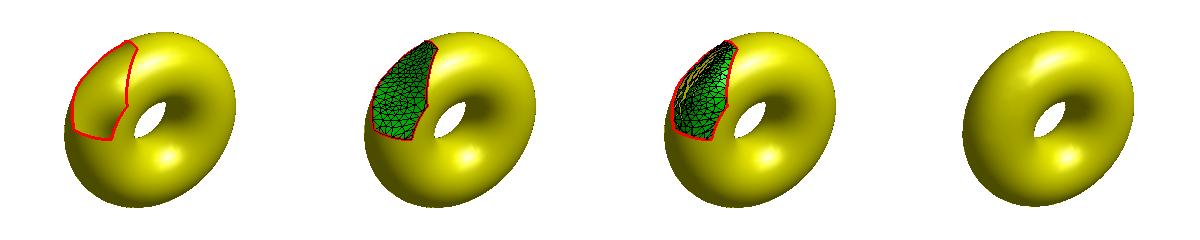
本文为原创，转载请注明出处：http://www.cnblogs.com/shushen

相关：

三维网格形变算法（Gradient-Based Deformation）：http://www.cnblogs.com/shushen/p/4932089.html

三维网格补洞算法（Radial Basis Function）：http://www.cnblogs.com/shushen/p/5759679.html

参考文献：

[1] Wei Zhao, Shuming Gao, and Hongwei Lin. 2007. A robust hole-filling algorithm for triangular mesh. Vis. Comput. 23, 12 (November 2007), 987-997.