【计算机算法设计与分析】——SVM

一.简介

支持向量机（support vector machines）是一种二分类模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。由简至繁的模型包括：

（1）当训练样本线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机；
（2）当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机；
（3）当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机；

二、线性可分支持向量机

1、间隔最大化和支持向量

如果一个线性函数能够将样本分开，称这些数据样本是线性可分的。那么什么是线性函数呢？其实很简单，在二维空间中就是一条直线，在三维空间中就是一个平面，以此类推，如果不考虑空间维数，这样的线性函数统称为超平面。我们看一个简单的二维空间的例子，O代表正类，X代表负类，样本是线性可分的，但是很显然不只有这一条直线可以将样本分开，而是有无数条，我们所说的线性可分支持向量机就对应着能将数据正确划分并且间隔最大的直线。

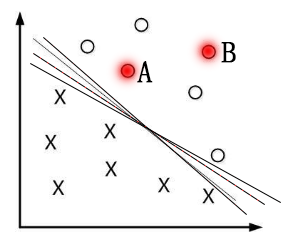
那么我们考虑第一个问题，为什么要间隔最大呢？一般来说，一个点距离分离超平面的远近可以表示分类预测的确信度，如图中的A B两个样本点，B点被预测为正类的确信度要大于A点，所以SVM的目标是寻找一个超平面，使得离超平面较近的异类点之间能有更大的间隔，即不必考虑所有样本点，只需让求得的超平面使得离它近的点间隔最大。
接下来考虑第二个问题，怎么计算间隔？只有计算出了间隔，才能使得间隔最大化。在样本空间中，划分超平面可通过如下线性方程来描述：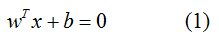

其中w为法向量，决定了超平面的方向，b为位移量，决定了超平面与原点的距离。假设超平面能将训练样本正确地分类，即对于训练样本(xi,yi)(xi,yi)，满足以下公式：

公式（2）称为最大间隔假设，yi=+1表示样本为正样本，yi=−1表示样本为负样本，式子前面选择大于等于+1，小于等于-1只是为了计算方便，原则上可以是任意常数，但无论是多少，都可以通过对 w 的变换使其为 +1 和 -1 ，此时将公式（2）左右都乘以 yi，得到如下：

实际上等价于：

训练集中的所有样本都应满足公式（3）。如下图所示，距离超平面最近的这几个样本点满足 yi(wTxi+b)=1，它们被称为“支持向量”。虚线称为边界，两条虚线间的距离称为间隔（margin）。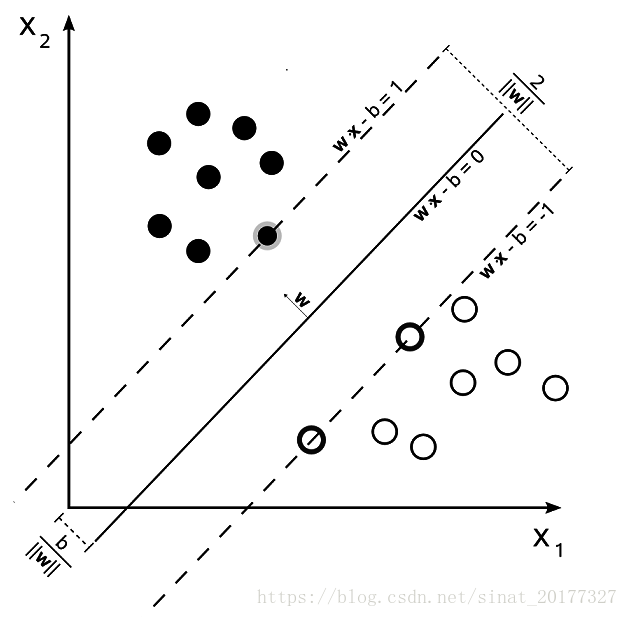

下面我们开始计算间隔，其实间隔就等于两个异类支持向量的差在 w 上的投影，即：

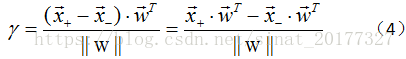
推出：

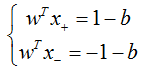
代入公式（4）中可以得到：

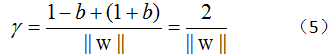
至此，我们求得了间隔，SVM的思想是使得间隔最大化，也就是：

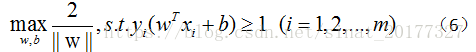
显然，最大化 2||w|| 相当于最小化 ||w||，为了计算方便，将公式（6）转化成如下：

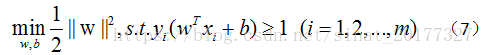
公式（7）即为支持向量机的基本型。

2、对偶问题

公式（7）本身是一个凸二次规划问题，可以使用现有的优化计算包来计算，但我们选择更为高效的方法。对公式（7）使用拉格朗日乘子法得到其对偶问题，该问题的拉格朗日函数可以写为：

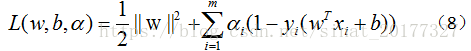
公式（8）分别对 w 和 b求偏导：

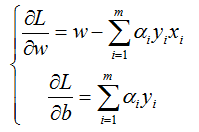
令其分别为0，可以得到：

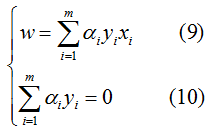
将公式（9）（10）代入公式（8），可得：

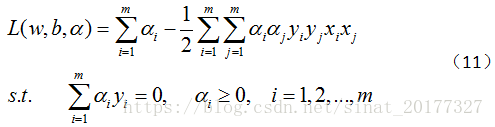
此时，原问题就转化为以下仅关于 α 的问题：

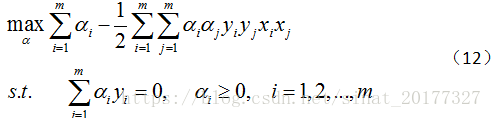
解出 α 之后，根据公式（9）可以求得 w ， 进而求得 b，可以得到模型：

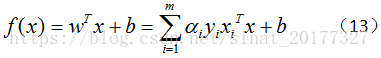
上述过程的KKT条件为：

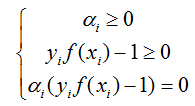
三、非线性支持向量机和核函数

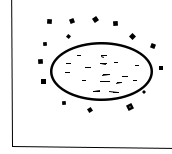
对于非线性问题，线性可分支持向量机并不能有效解决，要使用非线性模型才能很好地分类。先看一个例子，如下图，很显然使用直线并不能将两类样本分开，但是可以使用一条椭圆曲线（非线性模型）将它们分开。非线性问题往往不好求解，所以希望能用解线性分类问题的方法求解，因此可以采用非线性变换，将非线性问题变换成线性问题。

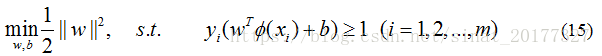
其对偶问题为：

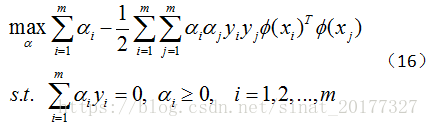
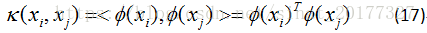
求解后得到：

四、线性支持向量机（软间隔支持向量机）与松弛变量

1、线性支持向量机

在前面的讨论中，我们假设训练样本在样本空间或者特征空间中是线性可分的，但在现实任务中往往很难确定合适的核函数使训练集在特征空间中线性可分，退一步说，即使瞧好找到了这样的核函数使得样本在特征空间中线性可分，也很难判断是不是由于过拟合造成。

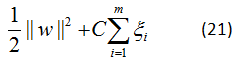
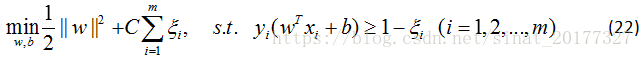
2、对偶问题

与线性可分支持向量机的对偶问题解法一致，公式（22）的拉格朗日函数为：

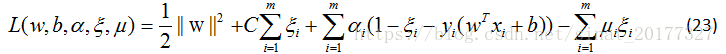
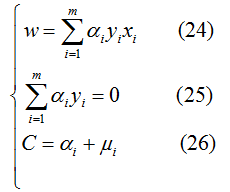
将公式（24）（25）（26）代入公式（23）得对偶问题：

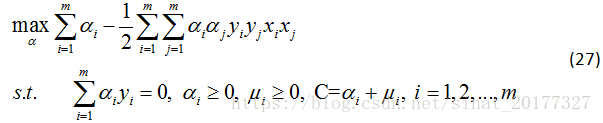
解出 α 之后，根据公式（9）可以求得 w ， 进而求得 b，可以得到模型：

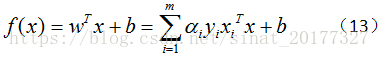
上述过程的KKT条件为：

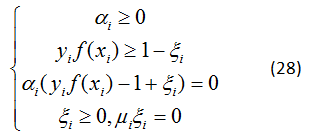
五、总结

至此，关于SVM的三类问题：

（1）线性可分支持向量机与硬间隔最大化

（2）非线性支持向量机与核函数

（3）线性支持向量机与软间隔最大化

　　我们所面对的所有的机器学算法，都是有适用范围的，或者说，我们所有的机器学习算法都是有约束的优化问题。而这些约束，就是我们在推导算法之前所做的假设。

比如：Logistics Regression，在Logistics Regression中，假设后验概率为Logistics 分布；再比如：LDA假设fk(x)是均值不同，方差相同的高斯分布；这些都是我们在推导算法之前所做的假设，也就是算法对数据分布的要求。

而对于SVM而言，它并没有对原始数据的分布做任何的假设，这就是SVM和LDA（经典的降维方法线性判别分析Linear Discriminant Analysis）、Logistics Regression区别最大的地方。这表明SVM模型对数据分布的要求低，那么其适用性自然就会更广一些。如果我们事先对数据的分布没有任何的先验信息，即，不知道是什么分布，那么SVM无疑是比较好的选择。

但是，如果我们已经知道数据满足或者近似满足高斯分布，那么选择LDA得到的结果就会更准确。如果我们已经知道数据满足或者近似满足Logistics 分布，那么选择Logistics Regression就会有更好的效果。

---------------------

感谢！
作者：ColiYin
来源：CSDN
原文：https://blog.csdn.net/sinat_20177327/article/details/79729551
版权声明：本文为博主原创文章，转载请附上博文链接！