算法：线性时间选择(C/C++)

Description

给定线性序集中n个元素和一个整数k，n<=2000000，1<=k<=n，要求找出这n个元素中第k小的数。

Input

第一行有两个正整数n,k. 接下来是n个整数（0<=ai<=1e9）。

Output

输出第k小的数

Sample Input

6 3
1 3 5 2 4 6

Sample Output

3

利用快速排序可以找出第k小的，加上随机函数改进一下：

#include <cstdio>
#include <cstdlib>
#include <ctime>
#include <iostream>

int num[2000001];

void quictSort(int, int, int);
int partition(int, int);

int main()
{
	int n, m, i;
	srand(unsigned(time(NULL)));		// 随机函数种子
	while (~scanf("%d%d", &n, &m))
	{
		for (i = 0; i < n; i++)
			scanf("%d", &num[i]);

		quictSort(0, n - 1, m - 1);

		printf("%d\n", num[m - 1]);
	}
	return 0;
}
// 快速排序
void quictSort(int left, int right, int mTop)
{
	if (left < right)
	{
		int p = partition(left, right);		// 分为两段

		if (p == mTop)						// 如果随机找到第mTop小就直接返回
			return;
		if (p < mTop)
			quictSort(p + 1, right, mTop);	// 找到的位置比mTop小就在[p + 1, right]区间找
		if (p > mTop)
			quictSort(left, p - 1, mTop);	// 找到的位置比mTop大就在[left, p - 1]区间找
	}
}
// 从小到大排
int partition(int left, int right)
{
	int r = rand() % (right - left + 1) + left;		// 随机选择一个数
	int key = num[r];
	std::swap(num[r], num[left]);					// 交换到数组首位
	while (left < right)
	{// 从数组后面开始, 找比随机选择的数小的, 然后从前找比随机选择的数大的
		while (left < right && num[right] >= key)
			right--;
		if (left < right)
			num[left] = num[right];

		while (left < right && num[left] <= key)
			left++;
		if (left < right)
			num[right] = num[left];
	}
	num[left] = key;		// 将随机选择的数存回
	return left;			// 返回随机选择的数分割数组的下标, 左边都是比它小的, 右边都是比它大的
}

中位数法线性时间选择划分：

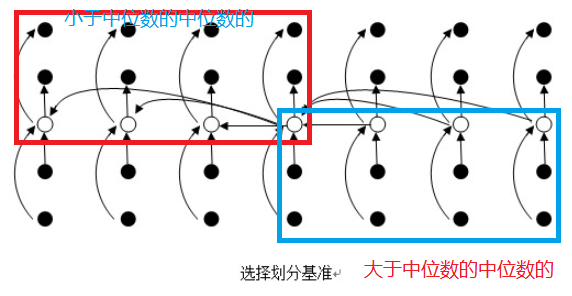
AC代码：

#include <cstdio>
#include <cstdlib>

int num[2000001];

int select(int low, int high, int top);
int partition(int low, int high, int median);
void selectSort(int low, int high);
void swap(int &a, int &b);

int main()
{
	int n, m, i;

	while (~scanf("%d%d", &n, &m))
	{
		for (i = 0; i < n; i++)
			scanf("%d", &num[i]);

		printf("%d\n", select(0, n - 1, m - 1));

		/*
		for (i = 0; i < n; i++)
			printf("%d%c", num[i], i < n - 1 ? ' ' : '\n');
		*/
	}
	return 0;
}
// 中位数法线性时间选择
int select(int low, int high, int top)
{
	// 小于75个数据随便用一个排序方法
	if (high - low < 74)
	{
		selectSort(low, high);				// 选择排序
		return num[low + top];				// 排完序直接返回第low + top的数
	}

	int groupNum = (high - low - 4) / 5;		// 每组5个数, 计算多少个组, 从0开始计数

	for (int i = 0; i <= groupNum; i++)
	{
		int start = low + 5 * i;				// 每组的起始位置
		int end = start + 4;					// 每组的结束位置
		for (int j = 0; j < 3; j++)				// 从小到大冒3个泡
			for (int k = start; k < end - j; k++)
				if (num[k] > num[k + 1])
					swap(num[k], num[k+1]);
		swap(num[low + i], num[start + 2]);		// 每组的中位数交换到前面第low + i的位置
	}
	// 上面排完后, 数组low + 0 到 low + groupNum都是每一组的中位数
	int median = select(low, low + groupNum, (groupNum + 1) / 2);	// 找中位数的中位数
	int p = partition(low, high, median);			// 将数组分为两段, 左边的小于中位数的中位数, 右边的大于中位数的中位数
	int n = p - low;			// 计算p到low之间有多少个数, 后面得减掉

	if (n == top)
		return num[p];			// 如果运气好, 刚好要找的就是中位数
	if (n > top)
		return select(low, p - 1, top);				// n比top大就在左边找
	if (n < top)
		return select(p + 1, high, top - n - 1);	// n比top小就在右边找, 并且top要减去已经大的个数
}
// 以中位数进行分割, 分成两半
int partition(int low, int high, int median)
{
	int p;
	for (int i = low; i <= high; i++)
		if (num[i] == median)
		{
			p = i;
			break;
		}
	// 将中位数交换到最前面
	swap(num[p], num[low]);
	// 记下最前面的数
	int key = num[low];
	// 把小于key的放前面, 大于key的放后面
	while (low < high)
	{
		while (num[high] >= key && low < high)
			high--;
		if (low < high)
			num[low] = num[high];
		while (num[low] <= key && low < high)
			low++;
		if (low < high)
			num[high] = num[low];
	}
	// 分别从两头开始, 找到中间时, 把key存回
	num[low] = key;
	return low;
}
// 选择排序
void selectSort(int low, int high)
{
	for (int i = low; i <= high; i++)
	{
		int MIN = i;
		for (int j = i + 1; j <= high; j++)
			if (num[MIN] > num[j])
				MIN = j;
		swap(num[i], num[MIN]);
	}
}
// 交换两个元素
void swap(int &a, int &b)
{
	int temp = a;
	a = b;
	b = temp;
}