【clustering】之K-means && K-medoids

k-means

k-medoids

一、clustering 中的 loss function

关于聚类的性能评价标准 参考博客

可以为外部指标和内部指标，其中外部指标是指 聚类结果与某个 “参考模型" 进行表示， 内部指标直接考察聚类结果不参考模型

• 外部指标：

1、Jaccard系数

系属于相同类占总类数的比例， 越大说明效果越好。

• 内部指标：

1、DB指数

DB计算 任意两类别的类内距离平均距离(CP)之和除以两聚类中心距离 求最大值

DB越小意味着类内距离越小 同时类间距离越大

• k-means 所要优化的目标函数

设我们一共有 N 个数据点需要分为 K 个 cluster ，k-means 要做的就是最小化 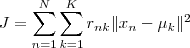这个函数，

其中  在数据点 n 被归类到 cluster k 的时候为 1 ，否则为 0 。

二、K值选取规则：

1、轮廓系数：

在实际应用中，由于Kmean一般作为数据预处理，或者用于辅助分聚类贴标签。所以k一般不会设置很大。可以通过枚举，令k从2到一个固定值如10，在每个k值上重复运行数次kmeans(避免局部最优解)，并计算当前k的平均轮廓系数，最后选取轮廓系数最大的值对应的k作为最终的集群数目。

轮廓系数讲解

2、Elbow method

对于n个点的数据集，迭代计算k from 1 to n，每次聚类完成后计算每个点到其所属的簇中心的距离的平方和，可以想象到这个平方和是会逐渐变小的，直到k==n时平方和为0，因为每个点都是它所在的簇中心本身。但是在这个平方和变化过程中，会出现一个拐点也即“肘”点，盗了张图可以看到下降率突然变缓时即认为是最佳的k值。

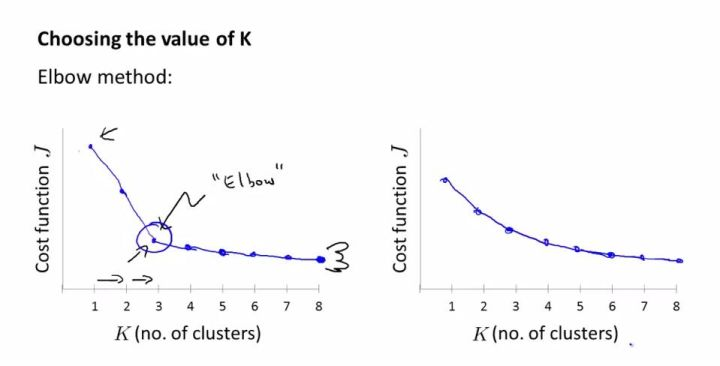
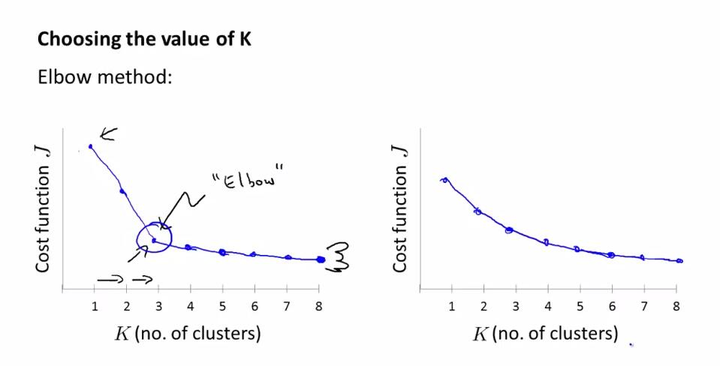
三、k-means与kmedoids

• k-means与k-medoids的不同之处

k-means在求聚类中心点时使用 均值 的方法来求的， k-medoids求聚类中心点时是用 中位数(质心） 的方法来求的，也就是说k-means的中心点是连续空间的值，而k-medoids是样本数据中的某一个。

• 为什么k-medoids用中位数？（k-medoid比k-means好在哪里）

1. 对于数值特征来说是没问题的，但是对于类别特征呢，这里举了一个对狗进行分类的栗子，相减，求均值就没什么意义，所以聚类中心点就从该cluster中选取，然后自定义一个衡量dissimilarity的函数，最终k-medoids的损失函数：，

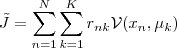最常见的方式是构造一个 dissimilarity matrix  来代表 ，其中的元素  表示第  只狗和第  只狗之间的差异程度，

2. k-medoids对噪声的鲁棒性更强，有一个噪声点，k-means很容易受影响，相反，k-medoids却没受多大影响

• k-medoids时间复杂度比k-means

k-medoids确定中位数时，需要n^2的时间，或者nlogn

局限性

1、受初始聚类点的影响

• 选择合适的初始点，可以加快算法的收敛速度和增强类之间的区分度
• 针对具体的问题有一些启发式的选取方法，或者大多数情况下采用随机选取的办法
• k-means 并不能保证全局最优，而是否能收敛到全局最优解其实和初值的选取有很大的关系，所以有时候我们会多次选取初值跑 k-means ，并取其中最好的一次结果。

参考博客：

http://blog.pluskid.org/?p=17