Git(创建与合并分支)

在版本回退里，你已经知道，每次提交，Git都把它们串成一条时间线，这条时间线就是一个分支。截止到目前，只有一条时间线，在Git里，这个分支叫主分支，即master分支。HEAD严格来说不是指向提交，而是指向master，master才是指向提交的，所以，HEAD指向的就是当前分支。

一开始的时候，master分支是一条线，Git用master指向最新的提交，再用HEAD指向master，就能确定当前分支，以及当前分支的提交点：

每次提交，master分支都会向前移动一步，这样，随着你不断提交，master分支的线也越来越长

演示视频：http://liaoxuefeng.gitee.io/git-resources/master-branch-forward.mp4

当我们创建新的分支，例如dev时，Git新建了一个指针叫dev，指向master相同的提交，再把HEAD指向dev，就表示当前分支在dev上：

你看，Git创建一个分支很快，因为除了增加一个dev指针，改改HEAD的指向，工作区的文件都没有任何变化！

不过，从现在开始，对工作区的修改和提交就是针对dev分支了，比如新提交一次后，dev指针往前移动一步，而master指针不变：

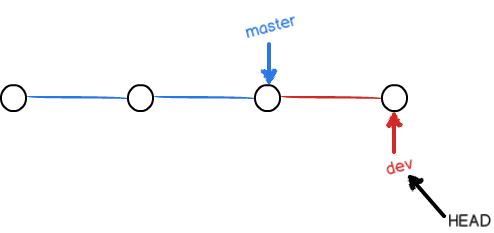
假如我们在dev上的工作完成了，就可以把dev合并到master上。Git怎么合并呢？最简单的方法，就是直接把master指向dev的当前提交，就完成了合并：

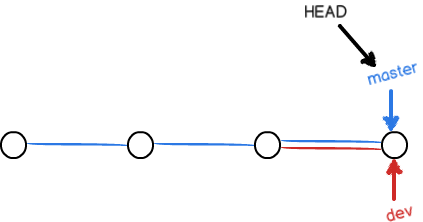
所以Git合并分支也很快！就改改指针，工作区内容也不变！

合并完分支后，甚至可以删除dev分支。删除dev分支就是把dev指针给删掉，删掉后，我们就剩下了一条master分支：

真是太神奇了，你看得出来有些提交是通过分支完成的吗？

视频地址：http://liaoxuefeng.gitee.io/git-resources/master-and-dev-ff.mp4

下面开始实战。

首先，我们创建dev分支，然后切换到dev分支：

git checkout命令加上-b参数表示创建并切换，相当于以下两条命令：

$ git branch dev
$ git checkout dev
Switched to branch 'dev'

然后，用git branch命令查看当前分支：

git branch命令会列出所有分支，当前分支前面会标一个*号。

然后，我们就可以在dev分支上正常提交，比如对readme.txt做个修改，加上一行：

Creating a new branch is quick.

然后提交：

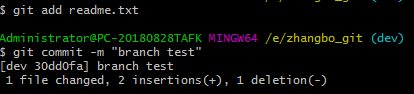
现在，dev分支的工作完成，我们就可以切换回master分支：

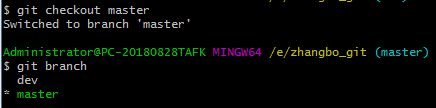
切换回master分支后，再查看一个readme.txt文件，刚才添加的内容不见了！因为那个提交是在dev分支上，而master分支此刻的提交点并没有变：

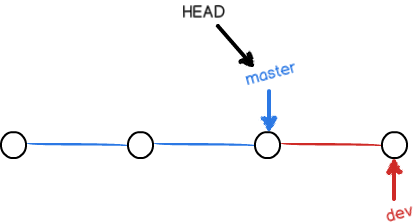
现在，我们把dev分支的工作成果合并到master分支上：

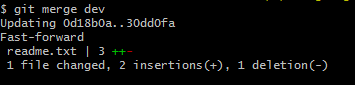
git merge命令用于合并指定分支到当前分支。合并后，再查看readme.txt的内容，就可以看到，和dev分支的最新提交是完全一样的。

注意到上面的Fast-forward信息，Git告诉我们，这次合并是“快进模式”，也就是直接把master指向dev的当前提交，所以合并速度非常快。

当然，也不是每次合并都能Fast-forward，我们后面会讲其他方式的合并。

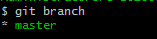
合并完成后，就可以放心地删除dev分支了：

删除后，查看branch，就只剩下master分支了：

因为创建、合并和删除分支非常快，所以Git鼓励你使用分支完成某个任务，合并后再删掉分支，这和直接在master分支上工作效果是一样的，但过程更安全

小结

Git鼓励大量使用分支：

查看分支：git branch

创建分支：git branch <name>

切换分支：git checkout <name>

创建+切换分支：git checkout -b <name>

合并某分支到当前分支：git merge <name>

删除分支：git branch -d <name>