[Bayesian] “我是bayesian我怕谁”系列 - Exact Inferences

要整理这部分内容，一开始我是拒绝的。欣赏贝叶斯的人本就不多，这部分过后恐怕就要成为“从入门到放弃”系列。

但，这部分是基础，不管是Professor Daphne Koller，还是统计学习经典，都有章节focus on这里。

可能这些内容有些“反人类正常逻辑”，故让更多的菜鸡选择了放弃。

《MLaPP》

参考《MLaPP》的内容，让我们打开坑，瞧一瞧。

20.2 Belief propagation for trees
In this section, we generalize the forwards-backwards algorithm from chains to trees. The resulting algorithm is known as belief propagation (BP) (Pearl 1988), or the sum-product algorithm.

读完这段话，第一感受是，要不要先看“前向后向算法"，再看此章。

Forwards-backwards algorithm在HMM中有提及，可以通过[Scikit-learn] Dynamic Bayesian Network - HMM学习。

打开A Tutorial Introduction to Belief Propagation，很快看到一个可能更为陌生的概念：马尔科夫条件随机场MRF。

没错，这种感觉就是机器学习领域中畅游的一个常见问题，交叉学科的通病，看到快高潮，陌生词汇来了，没了兴致。

所以，这篇文章的目的就是帮菜鸡去粗取精，讲那么多玩意干嘛，人生短暂，只学精华。

简单地讲，内容都是围绕条件概率，条件依赖关系，再弄明白Junction Tree Algorithm就完事。 那么，菜鸡们，走起？

提出问题

---

搞清楚“边缘条件概率”，例如：p( L | C = high )，本来有变量A到Z，现在只考虑L的概率，就是边缘分布；当时是在C = high 的条件下。

一般而言，穷举其他变量的所有情况，然后将概率相加即可。如下，有心情，有眼力，那你就算算。所以，这就是个需要解决的问题。

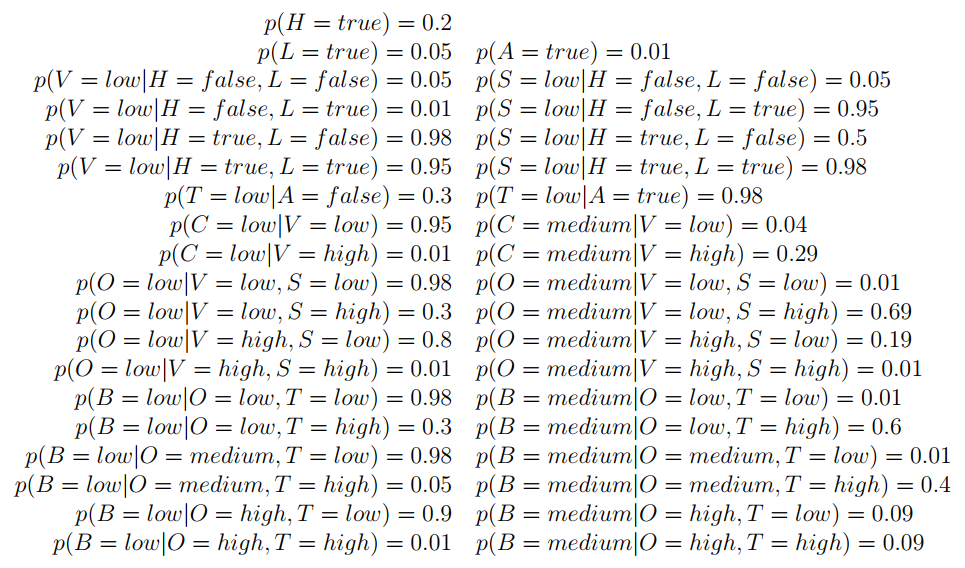
置信传播 Belief Propagation (BP) 

---

问题的方案之一便是这belief propagation。置信这个概念还出现在Deep Belief Networks - Geoffrey E. Hinton，可见不搞清楚这些细节的话，未来不好混。

过去不懂，现在了解”历史“的重要性。学习一个概念，了解其历史，极其有利于深入理解和掌握，这，可能也是很多人所欠缺的意识。

这段文字很好，原文可能来自于林达华，[ML] I'm back for Machine Learning中有介绍此牛人。能写出这段文字，可见其学识之广博。

是一个求解条件边缘概率(conditional marginal probability)的方法

Belief propagation是machine learning的泰斗J. Pearl的最重要的贡献。对于统计学来说，它最重要的意义就是在于提出了一种很有效的求解条件边缘概率(conditional marginal probability)的方法。说的有点晦涩了，其实所谓求解条件边缘概率，通俗地说，就是已知某些条件的情况下，推导另外某些事件发生的概率。

 

把全局的积分变成局部的消息传递

如果涉及的因素只有那么几个，一个学过概率论的大学生就可以使用简单的概率公式计算出来。可是，在现实世界中有成千上万的因素，它们相互联系，如果按照传统方法，就要对数以千计的变量进行积分。考虑到运算量对于变量个数以指数增长，因此这么做实际上根本没法算的。虽然，后来人们提出了蒙特卡罗(Monte Carlo)积分，但是对于拥有数以千计变量的复杂系统，仍然可以说是computationally prohibitive。

 

这个困难一直阻碍着统计推断方法在大规模系统中的应用。Belief propagation出来之后，情况才发生了转变。J. Pearl在他的书中分析说，人们在头脑中经常进行各种各样的推断，可是人在头脑里面发生了什么事情呢：穷举所有未知变量的可能状态进行积分(Traditional method)？还是随即产生各种状态求均值(Monte Carlo Integral)，看来都不make sense。J. Pearl认为，虽然影响世界的因素繁多，但是每个因素实际上只与少数几个因素相关，这就构成了一个推断网络。在machine learning里面，这样的网络有两种：Bayesian Network，反映的是因果推断关系（就是说，相互联系的因素中，其中一个是因，另外一个是果），以及Markov Network【条件随机场，无向图】， 反映的是相互影响的关系（两个因素互为因果，其变化相互影响）。根据这种建模方式，J.Pearl提出把inference局部化和分布化，把全局的积分变成局部的消息传递。网络中的每个节点通过和邻近节点交换信息对自身的概率状况进行评估。通过这种方式，使得计算量从指数增长变成近似的线性增长，从而使得统计推断能在复杂系统中被应用。

 

数学上可以证明，对于有向无环的Bayesian Network，可以证明，通过BP得到的解和严格的积分计算得到的结果是一致的。这时的BP只是利用因素联系的局部性来简化计算，并把计算过程分散到各个节点。对于无向而且到处是环的markov network，J.Pearl指出，这种传播过程是可能导致不稳定的。某些消息可能在环状的传播过程中无限加强，从而导致整个系统发散或者偏离。但是实际经验表明，对于大部分问题，BP在带环的系统中依然工作良好。很多人对这个现象进行了研究，对于某些特例给出了初步的解释，但是关于Loopy BP的稳定性和收敛性问题，离理论上的最终解决，还有很长的路要走。

 

思想的扩展：微观作用过程对于宏观状态形成的重要意义

在computer vision领域，MIT的著名教授W.T. Freeman是BP方法的积极倡导者，他大量使用markov random field和belief propagation对图像进行建模，在很多应用领域取得了不错的结果。

 

其实关于Local propagation的方法论，现在有超出了belief propagation的范畴。某些新的方法的优化流程也体现了类似的特征。我在我自己最近一项关于应用信息论进行监督学习的工作中发现，如果使用信息论最大化引导分类过程，事实上其优化流程就体现了样本间的局部交互和传播。不仅仅是机器学习，物理学也同样如此，比如当一个粒子发生了运动，其效应也是不断通过与邻近粒子的相互作用向外扩散，从而形成波动过程。一直以来，machine learning的formulation都是对问题从宏观着眼，可是最近一些工作都在暗示着微观作用过程对于宏观状态形成的重要意义。因此，一些新的研究开始偏向对局部结构和微观作用的考察，得到了一些有趣的发现。流形学习Manifold Learning中的一些重要方法，比如Local Linearly Embedding就是其中重要的代表。

是否有了点感性认识？

那么，再一起瞧一瞧原论文《Understanding belief propagation and its generalizations》从而更好地认识置信传播。

必要性：

这里也提到了“穷举的不利”。

要计算节点X的边缘概率，需要考虑其他节点所有的概率情况，然后都加起来，其实就是穷举法。

节点多了显然不合适，故采用BP，因为BP至少能够接近真实值。

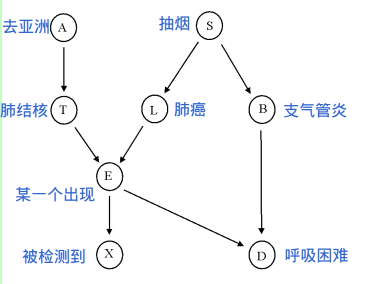
抽象化：

马尔科夫条件随机场MRF 作为实例进行讲解。

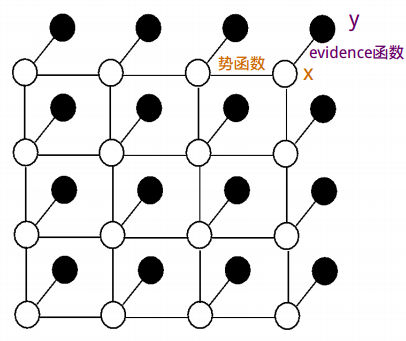
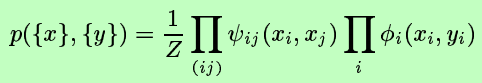
物理模型：

Ising model -->  物理模型，也便终于明白了“势函数”的由来。

将统计学习问题转化为“已知的”物理能量问题：local magnetizations。

物理的东西在此不做深究，但要有感性的认识。

到此为止，让概念不再陌生，虽不通透原理，但要明白它能带给我们什么功能、效果，会如何去用。

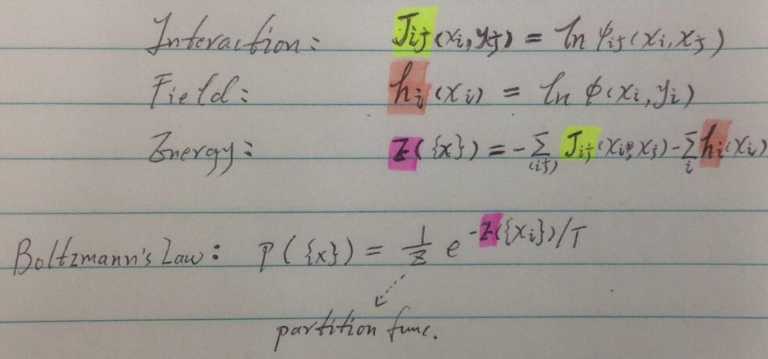
消息传递：

接下来的内容，基本就是讲解“消息传递”的过程，过程可见：[PGM] Exact Inference for calculating marginal distribution

在原论文中，也解释了链接方法2中那些个圆圈圈，方块块的缘由，起源于factor graph。

原理涉及一些物理能量背景，但我们只需要认识一个重要的结论即可：

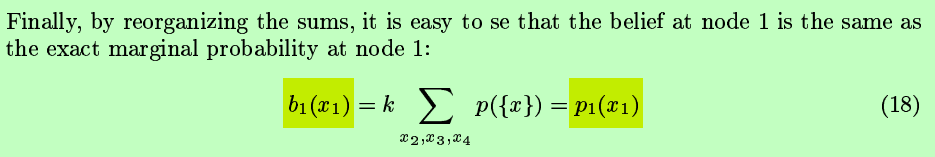
置信值等于了我们本要关心的边缘概率p₁(x₁) ！

置信传播在不同的情况下有不同的限制，但毕竟我们只考虑我们自己要解决问题时的情况，我们搞的是计算机，而不是物理也不是其他，所以，

我们只需要关注在一定条件下我们所需的那部分就好。比如：

“We have collected so far all the evidence to the node {V, S, O}.

The distribution of the evidence is not necessary as this node will not be further updated and it contains the required probability.”

在此，我们不考虑“消息反复震荡传递”这类复杂的情况，也没有必要，因为传一次我们的问题就解决了。

优越性

具体案例在[PGM] Exact Inference for calculating marginal distribution中体会。

大体上，一来看上去可以自动化。二来，在求边缘条件概率时，条件中一些没什么用处的变量似乎在过程当中便自动忽略掉了，穷举时变不用再去考虑这些变量，这样岂不是节省了计算资源。

简单的说，就是：穷举一些变量是不可避免，但你穷举的太多，我只穷举有必要的变量。

这便是链接中junction tree算法的贡献。

条件依赖关系 Conditional Independence

---

最重要的，就是搞清楚几个概念，以及相应的方法：

D-separation：[PGM] Bayes Network and Conditional Independence

这部分为变量消减做基础。

变量消减与置信传播又是[PGM] Exact Inference for calculating marginal distribution中的junction tree算法的基础。

所以，我们的最终目的就是求解“边缘条件概率”，例如：p( L | C = high )

如何减少不必要的计算，也就是提前干掉“没关系的变量”，只穷举有必要的。

最后的最后，花这么大力气，有什么产出没？

Professor Daphne Koller介绍了这款软件，不妨下载一试。

Samiam Download: http://reasoning.cs.ucla.edu/samiam/index.php?s=