树的平衡 AVL Tree

本篇随笔主要从以下三个方面介绍树的平衡：

1）：BST不平衡问题

2）：BST 旋转

3）：AVL Tree

一：BST不平衡问题的解析

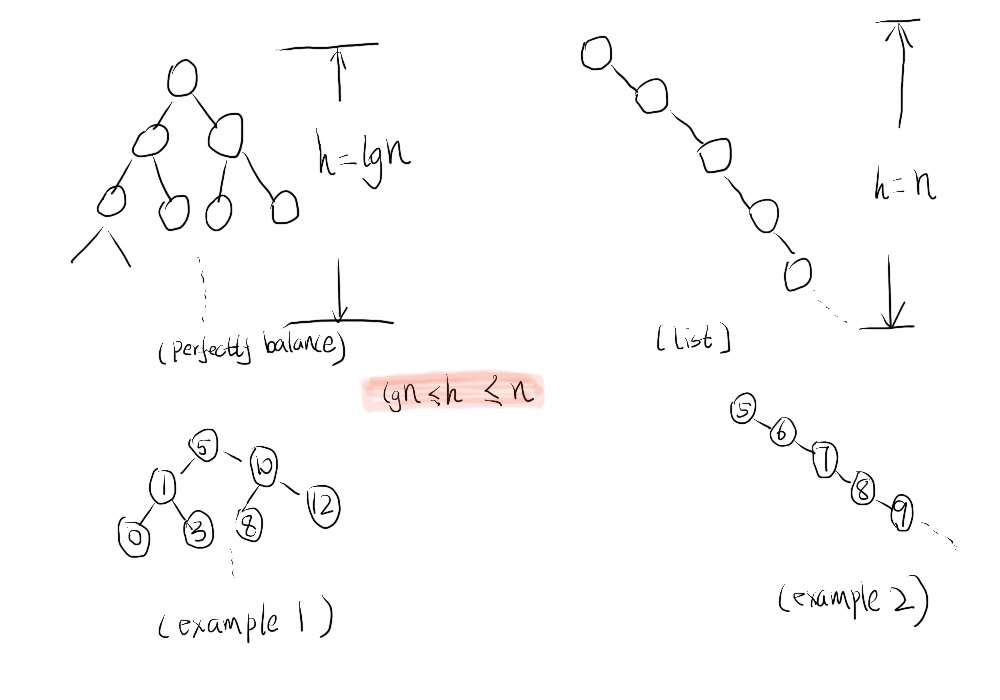
之前有提过普通BST的一些一些缺点，例如BST的高度是介于lgN和N之间的，如果是N的的话，显然效率很低，不是我们需要的；但是在实际情况中，BST的高度h = N的情况却经常出现，例如下图所示。在BST中search，insert的running time都等于BST的高度h，我们肯定希望高度h越小越好，best case就是lgN。下图的example 2的情况，我们会称之为这个BST是不平衡的。 所以如果遇到这种不平衡的BST，我们如何解决呢？如何将不平衡的BST转化成平衡的BST呢？如何将BST的高度h从N转化成lgN呢？

二：树的平衡

下面我们就来介绍一下树的旋转 rotation。BST是可以经过一些旋转操作后，仍然保持BST的结构不变的，即对于每一个node，该node的left child的值总是小于这个node的值，而该node的right child的值总是大于这个node的值。经过总结，这个旋转主要可以分为4中模式，这四种模式如下面的两图所示：

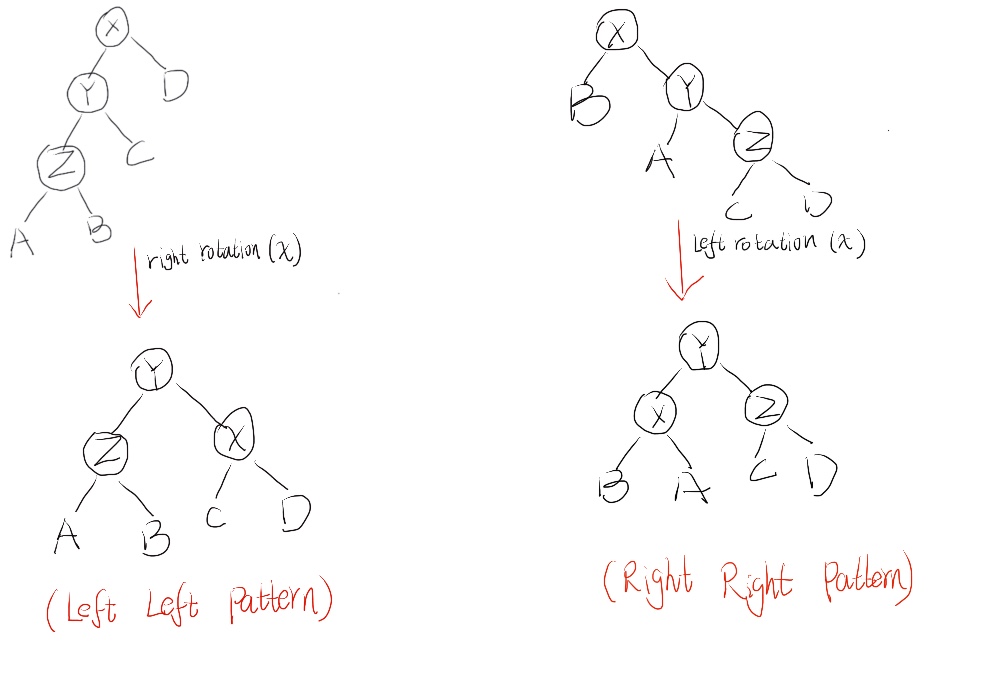
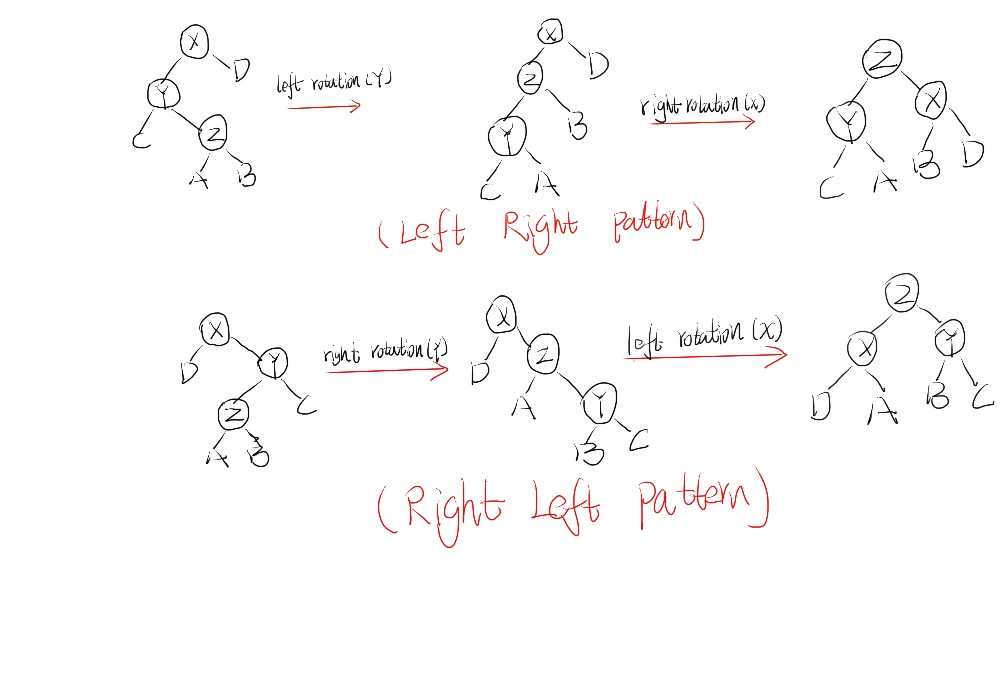
这四种rotation的方式是由BST的特性所决定的，至于为什么这样旋转是是正确的，也是由BST的特点所确定的，我在这就不证明了。只要大家记住BST可以有这4中旋转模式即可。其实上面所示的rotation过程，都是为了平衡树的目的。 那么现在有一个问题来了，我们说了这么多平衡，不平衡的概念，前面我们都是通过直观的感受来体味平衡或者不平衡，那么到底有什么明确的指标可以指明一个BST到底是平衡还是不平衡的呢？？？这个指标到底是什么呢？那么下面就要解释AVL Tree的概念了。

三：AVL Tree

首先AVL Tree要满足以下2个条件：

1. AVL Tree遵循BST的结构；即left child 小于当前node， right child大于当前node。

2.每一个node的2个 child nodes的高度相差不大于1。

根据上面的条件，我们可以看出AVL Tree其本质是一种特殊的BST。所以我们现在有一个定性的指标来判断一个BST是不是平衡的了，这个指标就是上面2个条件。当然了BST中有很多指标来判读一个BST是不是平衡的，我们这里只是用AVL Tree作为其中之一个指标，你也可以用其他的指标方法。

所以AVL Tree是平衡的，其高度是h=lgN;

在AVL Tree中，每一个node的高度等于取其2个child node 的较大的高度值加1，即max[left child height, right child height]+1; 若node==NULL，则其高度默认为-1.

当在构建AVL Tree的过程中，向其中insert node的时候，首先第一步跟BST insert一样，然后第二步是要检查insert后node的2个children之间的高度差，然后根据相应的高度差来判断相应的rotation的pattern，经过旋转后，使整个Tree仍然保持AVL Tree的特性，即满足上面的2个条件，所以仍然是平衡的。由于insert，search的操作的时间复杂度在BST中都是等于树的高度，AVL Tree作为一种特殊的BST，insert, search的操作的时间复杂度自然也是等于AVL的高度h=lgN. 这样的时间复杂度还是可以让我们满意的，其效率也要远远高于O（N）。AVL Tree的C++ 实现过程如下面的代码所示，以下代码实现了AVL Tree的insertion， sorting， rotation等功能。代码仅供学习交流等非盈利使用，不能用于商业目的，作者保留追溯的权利。

#include "AVLTree.hpp"
using namespace std;

AVL_Tree::AVL_Tree(){

    this->root = NULL;
}

void AVL_Tree::setRoot(Node *root){

    this->root = root;
}
Node *AVL_Tree::getRoot(){

    return this->root;
}

/*
 * height of tree or subtree
 *
 * a node's height equals the max of node's left child's height and node's right child's height plus 1
 *
 *parameters:
            1, node;//the node that we want to measure with
 *
 *return: the height of the node
 */
int AVL_Tree::height(Node *node){

    int h = -;

    if (node != NULL) {

        int l_height = height(node->getLeft());
        int r_height = height(node->getRight());
        h = std::max(l_height,r_height) + ;
    }

    return h;
}
/*
 * the height difference of two children nodes
 *
 *parameters:
 *          1, node;//the node which we want to know the differences of its two children
 *
 *return: int; the height difference of the two children nodes
 */

int AVL_Tree::heightDiff(Node *node){

    int l_height = height(node->getLeft());
    int r_height = height(node->getRight());

    return l_height-r_height;

}

/*
 *
 *4 types of rotations
 *
 *1)left left pattern
 *2)left right pattern
 *3)right right pattern
 *4)right left pattern
 *
 */
void AVL_Tree::ll_rotation(Node *node){

    int value = node->getData();
    Node *temp = node->getLeft();

    node->setData(temp->getData());
    node->setLeft(temp->getLeft());

    temp->setData(value);
    temp->setLeft(temp->getRight());
    temp->setRight(node->getRight());
    node->setRight(temp);

}
void AVL_Tree::lr_rotation(Node *node){

    Node *temp = node->getLeft();
    node->setLeft(temp->getRight());
    temp->setRight(temp->getRight()->getLeft());
    node->getLeft()->setLeft(temp);
    ll_rotation(node);

}
void AVL_Tree::rr_rotation(Node *node){

    int value = node->getData();
    Node *temp = node->getRight();

    node->setData(temp->getData());
    node->setRight(temp->getRight());

    temp->setData(value);
    temp->setRight(temp->getLeft());
    temp->setLeft(node->getLeft());
    node->setLeft(temp);

}
void AVL_Tree::rl_rotation(Node *node){

    Node *temp = node->getRight();
    node->setRight(temp->getLeft());
    temp->setLeft(node->getRight()->getRight());
    node->getRight()->setRight(temp);
    rr_rotation(node);

}

/*
 *Description: balancing the node whoes two children nodes' height difference is greater than 1 or smaller than -1
 *
 *parameters:
 *          1, node;//the node which we want to rotate with, it is the polar point of the rotation
 *
 *
 *return: void
 *
 *
 *
 */
void AVL_Tree::balance(Node *node){

    int balance_factor = heightDiff(node);//differences of the node's two sub nodes.

    if (balance_factor>) {//left side is heavy

        if (heightDiff(node->getLeft())>) {//left left case

            ll_rotation(node);

        }else{//left right case

            lr_rotation(node);
        }

    }else if (balance_factor<-){//right side heavy

        if (heightDiff(node->getRight())<) {//right right case

            rr_rotation(node);

        }else{//right left case

            rl_rotation(node);
        }

    }
}

/*
 * Description: insert a node into the AVL tree and keep the whole structure balanced after inserting
 *
 *Parameters:
 *          1, Node *node;//the node which needs to be inserted
 *          2, Node *root;//the root of the tree or subtree;
 *
 *Return: Node *;//the parent node of the inserted node;
 */

Node *AVL_Tree::insert(Node *node, Node *root){

    if (this->root == NULL) {

        Node *root = new Node();
        root->setLeft(NULL);
        root->setRight(NULL);
        root->setData(node->getData());
        this->root = root;

        return root;
    }

    if (root == NULL) {

        return node;

    }else if(node->getData() < root->getData()){

        root->setLeft(insert(node, root->getLeft()));
        balance(root);

    }else if (node->getData()>=root->getData()){

        root->setRight(insert(node, root->getRight()));
        balance(root);
    }

    return root;
}

/*
 *Description: print out the sorted nodes of the AVL tree of AVL subtree
 *
 *parameters:
 *          1, Node *node;//the root of the AVL tree of AVL subtree
 *
 *
 */
void AVL_Tree::inorderSort(Node *node){

    if (node == NULL) {

        return;
    }

    inorderSort(node->getLeft());
    std::cout<<node->getData()<<" ";
    inorderSort(node->getRight());

}