压缩感知中的数学知识：稀疏、范数、符号arg min

转自：http://blog.csdn.net/jbb0523/article/details/40262629

1、稀疏：什么是K稀疏呢?

在压缩感知里经常提到 “K稀疏” 的概念，这个是很容易理解的：也就是对于长度为N的向量（实际上是指一个N维离散离值信号）来说，它的N个元素值只有K个是非零的，其中K<<N，这时我们称这个向量是K稀疏的或者说是严格K稀疏的；实际中要做到严格K稀疏不容易，一般来说，只要除了这K个值其它的值很小很小，我们就认为向量是稀疏的，这时区别于严格K稀疏且就叫它K稀疏吧。

为什么要谈稀疏这个问题呢？因为如果信号是稀疏的，则它是可压缩的，也就是说里面那么多零，我只记录那些非零值及它的位置就好了。

当然，现实中的信号本身一般并不是稀疏的，但经过一个变换后，在一组基上面是稀疏的，这就是信号的稀疏表示。

稀疏性是压缩感知的前提。

2、范数||x||p

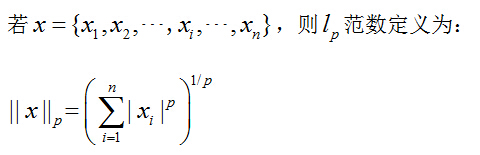
常见的有l0范数、l1范数、l2范数，经常要将l0范数等价为l1范数去求解，因为l1范数求解是一个凸优化问题，而l0范数求解是一个NP难问题，这些后面慢慢再说。

l0范数指的是x中非零元素的个数，即x的稀疏度，如果x是K稀疏的，则l0范数等于K；

l1范数指的是x中所有元素模值的和

l2范数指的是x中所有元素模值平方的和 再开方，这个带公式就可以了，它代表着距离的概念

还有无穷范数，指的是x中元素模的最大值

3、符号arg min

压缩感知中常见如下表示：

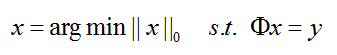
s.t. 表示 受约束于，是“subject to”的缩写。

为了说明argmin的含义，可以参见Wikipedia中对argmax的解释：

argmax : In mathematics, arg max stands for the argument of the maximum, that is to say, the set of points of the given argument for which the given function attains its maximum value.

（即求当满足约束条件时，使函数达到最大值的x）

举三个例子自己体会一下就可以了：

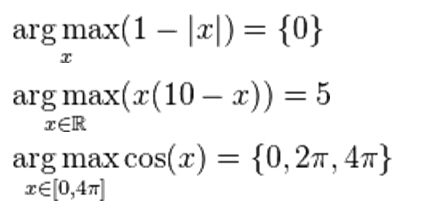
argmin与其类似，琢磨一下就是了。

下面转一段话：（max 和 argmax的区别）

y = f(t) 是一般常见的函数式，如果給定一个t值，f（t）函数式会赋一个值給y。

y = max f(t) 代表：y 是f(t)函式所有的值中最大的output。

y = arg max f(t) 代表：y 是f(t)函式中，会产生最大output的那个参数t。

看起来很模糊，举个例子应该比较好理解：

假设有一个函式 f(t)，t 的可能范围是 {0,1,2}，f(t=0) = 10 ;
f(t=1) = 20 ; f(t=2) = 7，那分別对应的y如下：

y = max f(t) = 20

y= arg max f(t) = 1

这一块要好好说一说，因为这是压缩感知最基本的表示，是最常见的，但在不同的论文里面表示是不统一的：

a)焦李成，杨淑媛，刘芳，侯彪.压缩感知回顾与展望[J].电子学报，2011，39(7)：1651-1662.

b)石光明，刘丹华，高大化，刘哲，林杰，王良君.压缩感知理论及其进展[J].电子学报，2009，37(5)：1070-1081.

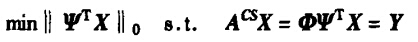
c)杨海蓉，张成，丁大为，韦穗.压缩传感理论与重构算法[J].电子学报，2011，39(1)：142-148.

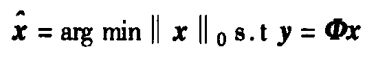
在压缩感知理论方面，不管是用min还是argmin（文献ab与文献c区别），不管min下面有没有变量（文献a与文献b区别），其实表达的意思都是一样的：

如果用0范数，则是求得满足后面约束条件的最稀疏的x(或θ)；

如果用1范数，则是求得满足后面约束条件的元素模值和最小的x(或θ)；

当然两种求法在满足一定条件下(RIP)是等价的，RIP又是另一回事了，慢慢以后再说吧。