分岔 Bifurcations

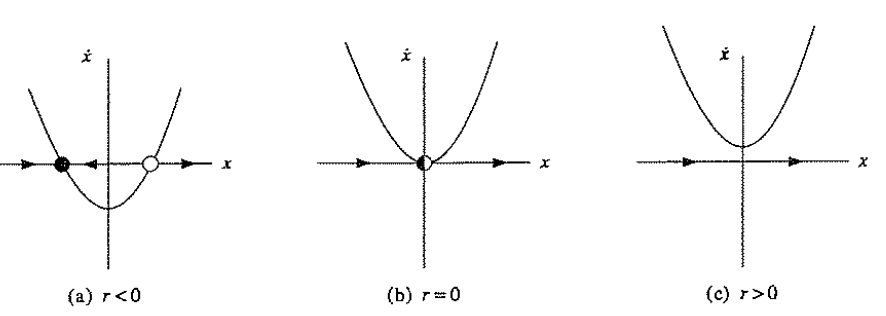
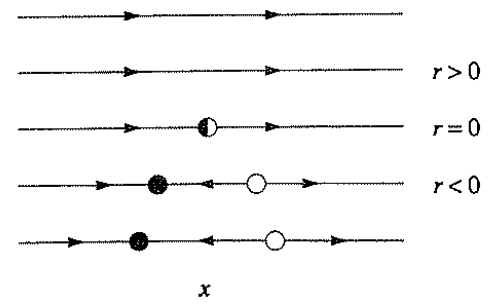
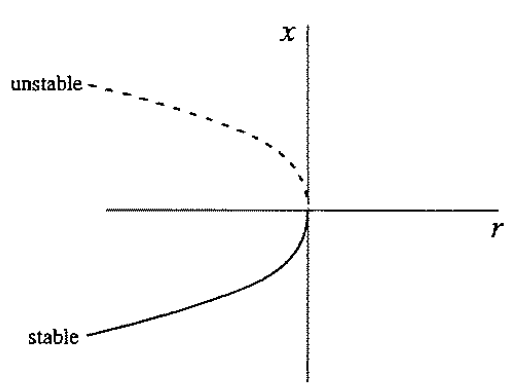
1. saddle-node bifurcation

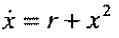
2. transcritical bifurcation

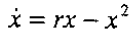
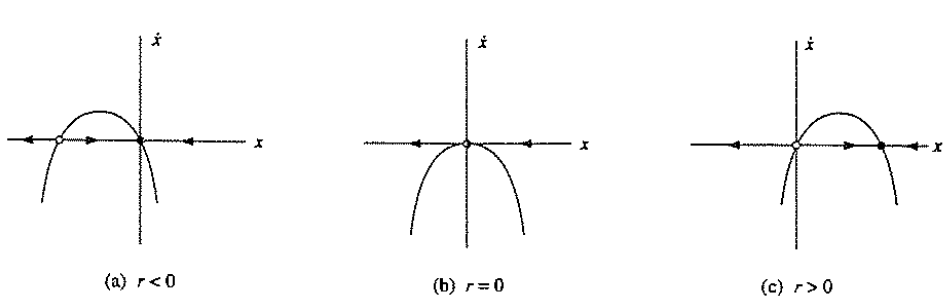
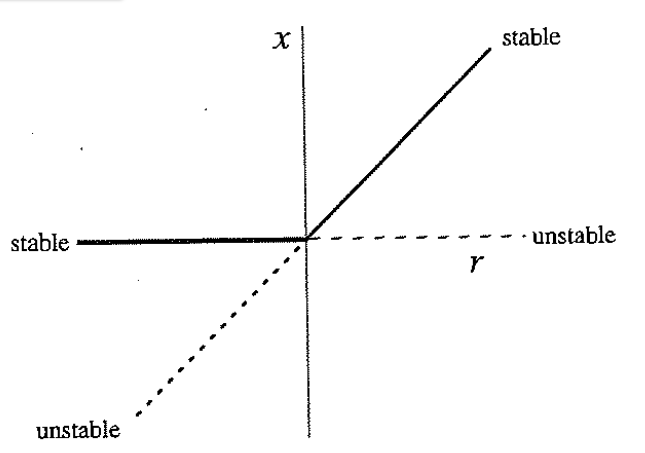
3.pitchfork bifurcation

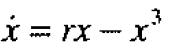
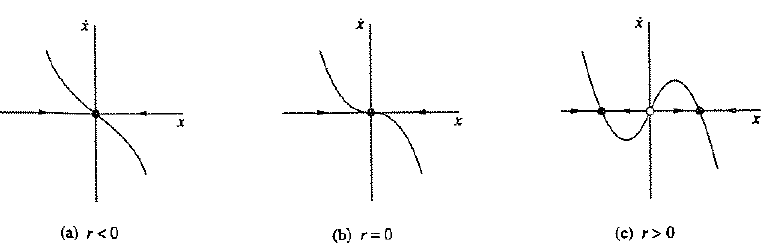
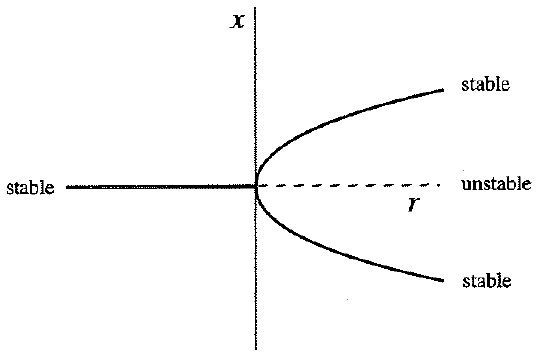
4. Hopf bifurcation

作者：许铁-巡洋舰科技
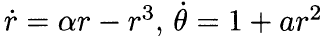
链接：https://www.zhihu.com/question/26359793/answer/133232527
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

To be or Not to be，That is a Bifurcation ！

Hopf-Bifurcation : 沟通平衡与振动的世界。

用一句话说， Hopf-Bifurcation 描述一个系统定点失去吸引力并最终产生闭合轨道的过程。 这与我开头引题的抛物线那个图其实是一回事，我们把非线性系统在定点附近进行线性近似就可以沿用上面的分析。

BZ反应 (Belousov Zhabotinsky 化学反应)

我们高中课本有个东西叫化学平衡， 说的是化学过程最终都导致平衡，该反应的反应过了，我们就得到一堆万年不变的反应产物。 但是1950年代的一个苏联科学家belousov却在它的反应里发现了一个十分惊人的现象， 他发现他手里的混合物反应后还会在一段时候回到原来的状态，然后又重新反应，如此周期反复。这一现象一出，他就被封杀了。因为他的结果不符合热力学第二定律（根据热力学第二定律，自发状态下系统必须趋于平衡），又加上适逢冷战，他到死也没看到他的成果被承认，成为科学史上几个重大悲剧之一。

但是它的发现却开拓了一个全新的领域-化学振荡，而他的发现也成为复杂性可以从简单系统中诞生的典型例子，与图灵对生物斑图的研究一起，开拓了复杂科学的先河。

<img src="https://pic2.zhimg.com/809ceaf5a2a3db2eb9cbaac672e2ca61_b.png" data-rawwidth="778" data-rawheight="503" class="origin_image zh-lightbox-thumb" width="778" data-original="https://pic2.zhimg.com/809ceaf5a2a3db2eb9cbaac672e2ca61_r.png">

周期振荡的化学反应，红变蓝又变红。

<img src="https://pic4.zhimg.com/a39296bf27a4e1ee7bf531bdfe741fd7_b.png" data-rawwidth="285" data-rawheight="279" class="content_image" width="285">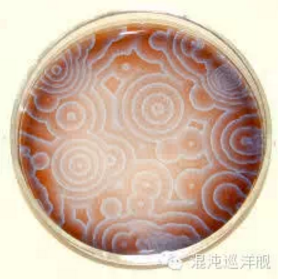

Belousov的化学振荡可以自发产生美丽复杂的斑图（上图），被认为是复杂性从简单系统产生的典范。 对生命起源等问题都很有启发。

如果我们给这个化学反应写出热力学方程，我们就可以发现，循规蹈矩的化学平衡和“异常”的化学振荡可以完全统一在一个系统里，只是根据反应物浓度不同而不同。 它的本质即Hopf Bifurcation。

Belousov反应具有众多反应物和接近20个步骤，但是可以简化为一个二维动力学系统（内容繁杂在此不续）：

<img src="https://pic1.zhimg.com/d78b61a311d24432c61530eda51c3390_b.png" data-rawwidth="787" data-rawheight="439" class="origin_image zh-lightbox-thumb" width="787" data-original="https://pic1.zhimg.com/d78b61a311d24432c61530eda51c3390_r.png">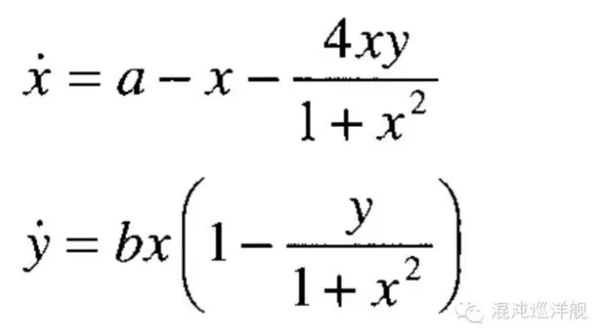

随着参数a，b的变化系统具有完全不同的动力学模型，见下图：

<img src="https://pic1.zhimg.com/af8c09724bf4d8e56db950ec58017668_b.png" data-rawwidth="809" data-rawheight="287" class="origin_image zh-lightbox-thumb" width="809" data-original="https://pic1.zhimg.com/af8c09724bf4d8e56db950ec58017668_r.png">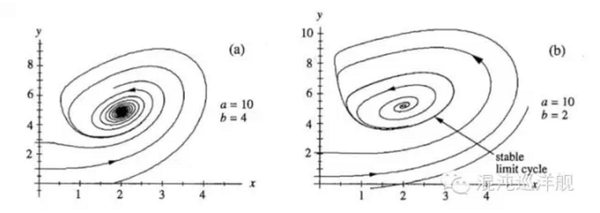

Hopf Bifurcation， 左图是一个具有静止平衡态（定点）的系统，动力学流从不同的位置旋入这个系统。 右图为振动解（limit cycle）的诞生， 事实上，两张图描述的是一个系统的连续变化，开始那个稳定的平衡点失去稳定属性，流行从旋入这个点变为旋出，而归于确定的闭合轨道。这就是Hopf Bifurcation的范式。

Hopf Bifurcation 作为阐述振动和静态平衡互相演化的基本手段， 在生物，经济等领域反复出现。

5. 二维动力系统 

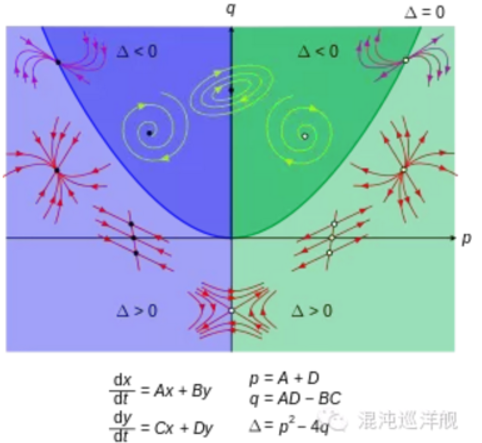
二维动力系统：例如下图里的那个抛物线， 当系统的参数变化越过抛物线的时候，系统就从稳定吸引变成了发散远离定点，这个过程就是Bifurcation.

而在抛物线一侧的变化只是定量的变化，却无定性改变，这就是普通的变化。Bifurcation标志系统的动力学性质就发生彻底的变化。好比两个人在一条路上走着走着，突然到了岔路口，从此南辕北辙。