Codeforces Round #597 (Div. 2) D. Shichikuji and Power Grid 题解 最小生成树

题目链接：https://codeforces.com/contest/1245/problem/D

题目大意：

平面上有n座城市，第i座城市的坐标是 \(x[i], y[i]\) ，

你现在要给n城市供电，对于第i座城市，你可以选择两种方式给其供电：

• 建造一个发电站供电，这需要花费 \(c[i]\) ；
• 连一条连向城市j的电缆，这需要花费 \((|x[i]-x[j]|+|y[i]-y[j]|) \times (k[i]+k[j])\) 。

现在告诉你n以及 \(x[i], y[i], c[i], k[i]\) ，请你求出以下信息：

• 最少花费；
• 自己发电的城市数量；
• 自己发电的城市编号；
• 城市间连接电缆的数量；
• 所有连接有电缆的城市对。

解析思路：

这道题目就是一道最小生成树裸题。

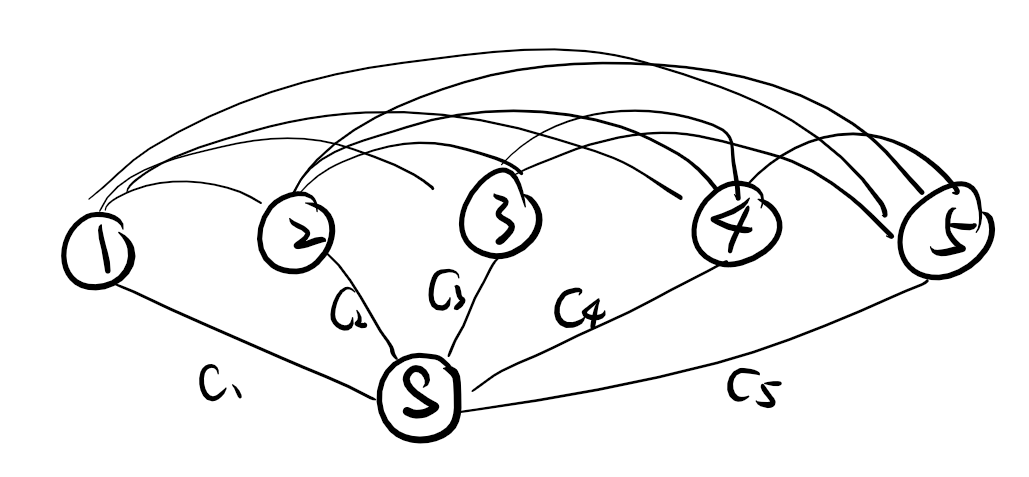
首先，除了 \(n\) 个节点以外，我再开一个点 \(S\)（在我的程序中 \(S = 0\)），然后将 \(n\) 个点中的任意一点 \(i\) 分别向 \(S\) 连一条权值为 \(c[i]\) 的边，

\(n\) 个点两两之间（设两点编号为 \(i\) 和 \(j\)）连一条权值为 \((|x[i]-x[j]| + |y[i]-y[j]|) \times (k[i]+k[j])\) 的边。

然后求这 \(n+1\) 个点的最小生成树。

整个图大致如下：

然后在最小生成树的 \(n\) 条边中，如果这条边的一个端点是 \(S\) ，那么另一个端点 \(i\) 就是自己建站的；

否则，这条边上的两点就是有连接关系的。

这样就能得到题目所要求的所有数据。

实现最小生成树可以使用kruskal或者prim算法，我这里使用kruskal实现。

实现代码如下：

#include <bits/stdc++.h>
using namespace std;
#define INF (1<<29)
const int maxn = 2020, maxm = 5000500;
struct Edge {
    int u, v;
    long long w;
    Edge() {}
    Edge(int _u, int _v, long long _w) { u = _u; v = _v; w = _w; }
} edge[maxm];
long long x[maxn], y[maxn], c[maxn], k[maxn], cost[maxn];
int n, cnt, f[maxn];
vector<int> res1;
vector<pair<int, int> > res2;
bool cmp(Edge a, Edge b) { return a.w < b.w; }
void init() {
    for (int i = 0; i <= n; i ++) f[i] = i;
}
int func_find(int x) {
    return x == f[x] ? x : f[x] = func_find(f[x]);
}
void func_union(int x, int y) {
    int a = func_find(x), b = func_find(y);
    f[a] = f[b] = f[x] = f[y] = min(a, b);
}
void kruskal() {
    init();
    sort(edge, edge+cnt, cmp);
    int cc = 0;
    long long ans = 0LL;
    for (int i = 0; i < cnt; i ++) {
        int u = edge[i].u, v = edge[i].v;
        long long w = edge[i].w;
        // printf("u = %d , v = %d , w = %lld\n", u, v, w);
        if (func_find(u) != func_find(v)) {
            ans += w;
            cc ++;
            if (!u) res1.push_back(v);
            else if (!v) res1.push_back(u);
            else res2.push_back(make_pair(u, v));
            func_union(u, v);
            if (cc == n) break;
        }
    }
    cout << ans << endl;
}
int main() {
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> x[i] >> y[i];
    for (int i = 1; i <= n; i ++) cin >> c[i];
    for (int i = 1; i <= n; i ++) cin >> k[i];
    for (int i = 1; i <= n; i ++) edge[cnt++] = Edge(0, i, c[i]);
    for (int i = 1; i <= n; i ++) for (int j = 1; j <= n; j ++) edge[cnt++] = Edge(i, j, (abs(x[i]-x[j])+abs(y[i]-y[j]))*(k[i]+k[j]));
    kruskal();
    int sz = res1.size();
    cout << sz << endl;
    for (int i = 0; i < sz; i ++) {
        if (i) putchar(' ');
        cout << res1[i];
    }
    cout << endl;
    sz = res2.size();
    cout << sz << endl;
    for (int i = 0; i < sz; i ++) {
        cout << res2[i].first << " " << res2[i].second << endl;
    }
    return 0;
}