Mondriaan's Dream 轮廓线DP 状压

Mondriaan's Dream

题目链接

Problem Description

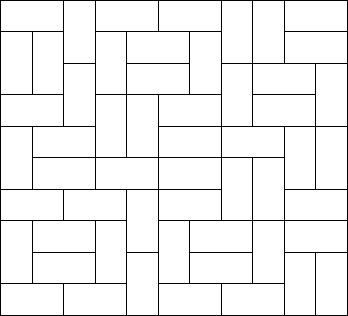
Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.



Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare!

Input

The input file contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11.

Output

For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

Sample Input

1 2

1 3

1 4

2 2

2 3

2 4

2 11

4 11

0 0

Sample Output

1

0

1

2

3

5

144

51205

经典的一道轮廓线dp题

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
#define inf 0x3f3f3f3f
const ll INF = 0x3f3f3f3f3f3f3f3f;
const ll MAXN = 1e6 + 7;
const ll MAXM = 1e3 + 7;
const ll MOD = 1e9 + 7;
const double eps = 1e-6;
int n, m, cur;
ll dp[2][1 << 15]; //滚动数组
void update(int from, int to)
{
    if (to & (1 << m)) //判断溢出的一位是不是1，是0则不合法
        dp[cur][to ^ (1 << m)] += dp[cur ^ 1][from];
}
int main()
{
    while (~scanf("%d%d", &n, &m) && n && m)
    {

        if ((n * m) & 1) //总格子是奇数自然不行
            printf("0\n");
        else
        {
            cur = 0;
            if (m > n)
                swap(n, m);
            int top = 1 << m;
            dp[cur][top - 1] = 1; //轮廓线上方
            for (int i = 0; i < n; i++)
            {
                for (int j = 0; j < m; j++)
                {
                    cur ^= 1;
                    memset(dp[cur], 0, sizeof(dp[cur]));
                    for (int k = 0; k < top; k++) /* 转移轮廓线上的状态 */
                    {
                        /* 不放 直接转移*/
                        update(k, k << 1);
                        /* 往上放 上为0,当I=0时不可往上摆*/
                        if (i && !(k & (1 << m - 1)))
                            update(k, (k << 1) ^ (1 << m) ^ 1);
                        /* 往左放 左为0,上为1 ,j=0时不可往左摆*/
                        if (j && !(k & 1))
                            update(k, (k << 1) ^ 3);
                    }
                }
            }
            printf("%lld\n", dp[cur][(1 << m) - 1]);
        }
    }
    return 0;
}