学习JDK1.8集合源码之--ArrayDeque

1. ArrayDeque简介

　　ArrayDeque是基于数组实现的一种双端队列，既可以当成普通的队列用（先进先出），也可以当成栈来用（后进先出），故ArrayDeque完全可以代替Stack，ArrayDeque是非线程安全的，Stack是线程安全的。

　　ArrayDeque虽然是基于数组实现的，但很容易被数组这种数据结构所迷惑。因为数组是从0开始到length-1位置结束的，但ArrayDeque的实现实际上是一种循环结构的队列，首尾位置完全靠head和tail两个首尾指针来决定的，正常理解的情况下head的值应该比tail小，但是这里会出现head比tail大的情况。所以这里我们不能以正常数组的角度去看待，我可以把这个数组看成一个环形结构的首尾相连的结构，即数组最后一位的下一位就是第一位（不要习惯性把0当成头部，length-1当成尾部），数据都存储在head右边及tail的左边，不知道有没有说清楚~~

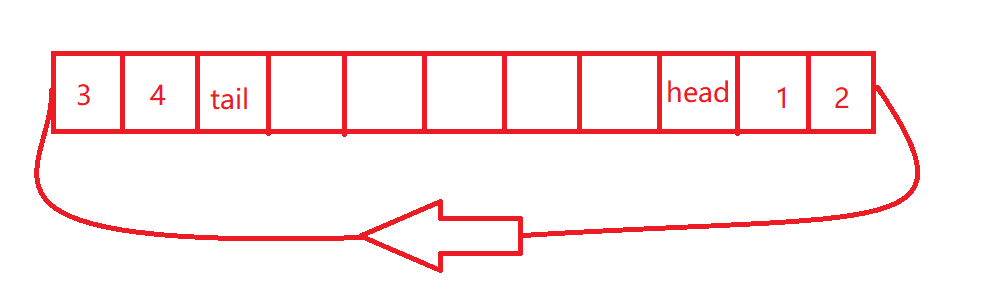
　　除此之外，ArrayDeque对队列的容量有特殊的要求，必须是2^n（这里和HashMap类似），由于2^31超出int的最大值，故ArrayDeque的最大容量为2^30。ArrayDeque不允许存储null值，原因是需要通过取出的元素是否为null来判断队列是否为空。

　　关于更多关于ArrayDeque的讲解，这篇文章讲的很好：【源】ArrayDeque，Collection框架中不起眼的一个类

2. ArrayDeque继承关系

　　ArrayDeque继承自AbstractCollection，实现了Deque、Cloneable、java.io.Serializable接口。

　　继承自AbstractCollection表明ArrayDeque是一个集合，并且拥有AbstractCollection的全部API。

　　实现了Deque接口，表明ArrayDeque是一个双端队列，实现了双端队列相关操作。

　　实现了Cloneable接口：可以调用Object.clone方法返回该对象的浅拷贝。

　　实现了 java.io.Serializable 接口：可以启用其序列化功能，能通过序列化去传输。

3. ArrayDeque实现

1. 核心参数

    //存储数据，同包类可访问，不可被序列化
    transient Object[] elements;
    //头部指针，不可被序列化
    transient int head;
    //尾部指针，不可被序列化
    transient int tail;
    //最小初始容量
    private static final int MIN_INITIAL_CAPACITY = 8;

　　ArrayDeque底层通过数组进行数据存储，通过head和tail两个指针实现了双端队列，并且定义了最小的初始容量为8。

2. 构造方法

    //无参构造，默认创建一个容量为16的数组
    public ArrayDeque() {
        elements = new Object[16];
    }

    //传入一个数值，根据这个数值计算出适合的初始容量
    public ArrayDeque(int numElements) {
        allocateElements(numElements);
    }

    //传入一个集合，根据集合的大小计算出合适的初始容量，并将集合中的所有元素添加进来
    public ArrayDeque(Collection<? extends E> c) {
        allocateElements(c.size());
        addAll(c);
    }

3. 核心方法

    //这里为什么用private static修饰？
    //通过一系列位运算得到大于numElements的最小2的次幂
    private static int calculateSize(int numElements) {
        int initialCapacity = MIN_INITIAL_CAPACITY;
        //如果numElements >= initialCapacity则计算合适的初始容量，否则直接返回默认初始容量
        if (numElements >= initialCapacity) {
            initialCapacity = numElements;
            //与'+='符号类似，a |= b 等效于 a = a | b, 这里进行的是二进制的或运算
            //假设initialCapacity = 24, 二进制数值为 00011000;
            //initialCapacity >>> 1 二进制数值为 00001100;
            // 00011000 | 00001100 = 00011100; 28
            initialCapacity |= (initialCapacity >>>  1);
            // 00011100 >>>  2 = 00000111;
            // 00011100 | 00000111 = 00011111; 31
            initialCapacity |= (initialCapacity >>>  2);
            //00011111 >>> 4 = 00000001;
            //00011111 | 00000001 = 00011111; 31
            initialCapacity |= (initialCapacity >>>  4);
            //...
            initialCapacity |= (initialCapacity >>>  8);
            initialCapacity |= (initialCapacity >>> 16);
            //int为32位 通过这连续几次左移操作总共左移了31位（1+2+4+8+16 = 31）
            //将二进制数从第一个不为0的位开始后面每一位都变成1
            //最后再加1取得比numElements大的最小2的次幂
            initialCapacity++;

            //initialCapacity超出int最大值时，左移一位（除以2），最大容量为2 ^ 30
            if (initialCapacity < 0)
                initialCapacity >>>= 1;
        }
        return initialCapacity;
    }

    //新建一个数组来保证容量足够容纳numElements个元素
    private void allocateElements(int numElements) {
        elements = new Object[calculateSize(numElements)];
    }

    //将底层数组扩容1倍
    private void doubleCapacity() {
        //断言，当head == tail为true时才会向下执行，否则抛出AssertionError并终止执行
        //当head == tail时表明底层数组已经满了
        assert head == tail;
        int p = head;
        // 记录数组的长度
        int n = elements.length;
        //这里取head右边数据的个数，由于是双端队列，数据从数组两端都可以添加数据（这里的数组可以看成首尾相连的循环数组，即element.length + 1 = 0）
        //既可以在下标为0的位置开始向后添加元素，也可以从n-1位置依次向前添加元素
        //如addFirst方法是从数组最后一位开始添加数据的，head初始值为0，第一次调用时会变成n，之后每添加一次head-1
        //addLast方法则从第一位开始添加数据，tail初始值为0，每次添加元素tail+1
        int r = n - p; // number of elements to the right of p
        // 将数组长度扩大2倍
        int newCapacity = n << 1;
        //如果扩容后超出int最大值则抛出异常
        if (newCapacity < 0)
            throw new IllegalStateException("Sorry, deque too big");
        //新建一个数组，容量为当前前的2倍
        Object[] a = new Object[newCapacity];
        //将head后面的元素拷贝到新数组的开始位置
        System.arraycopy(elements, p, a, 0, r);
        //将head前面的元素拷贝到新数组的开始位置
        System.arraycopy(elements, 0, a, r, p);
        //将底层数组替换成扩容后的数组
        elements = a;
        //head重置为0
        head = 0;
        //tail重置为最后一个位置索引+1
        tail = n;
    }

    //内部拷贝元素
    private <T> T[] copyElements(T[] a) {
        //双端循环队列，元素存在head右边和tail的左边
        //当head<tail时，元素都存在数组head和tail位置之间，只需要进行一次拷贝
        if (head < tail) {
            System.arraycopy(elements, head, a, 0, size());
        //否则数组中，head和tail位置之间是没有元素存储的，不是连续的，需要分2次拷贝
        } else if (head > tail) {
            int headPortionLen = elements.length - head;
            System.arraycopy(elements, head, a, 0, headPortionLen);
            System.arraycopy(elements, 0, a, headPortionLen, tail);
        }
        return a;
    }

    //从队列头部添加元素e，插入null元素会报空指针异常
    public void addFirst(E e) {
        if (e == null)
            throw new NullPointerException();
        //如果elements.length = 16，则 element.length - 1 = 15,转为二进制 00000000 00000000 00000000 00001111
        //第一次添加时head=0 head - 1 = -1 （1的反码再取补码）转为二进制 11111111 11111111 11111111 11111111
        //   00000000 00000000 00000000 00001111
        // & 11111111 11111111 11111111 11111111
        // = 00000000 00000000 00000000 00001111 （15）
        //第二次添加时head=15 head - 1 = 14 转为二进制 00000000 00000000 00000000 00001110
        //   00000000 00000000 00000000 00001110
        // & 11111111 11111111 11111111 11111111
        // = 00000000 00000000 00000000 00001110 （14）
        //从上面可以看出，head = (head - 1) & (elements.length - 1)实际上就是从数据最后一位开始依次向前添加元素
        elements[head = (head - 1) & (elements.length - 1)] = e;
        //当head==tail时说明数组已经装满了，需要进行扩容
        if (head == tail)
            doubleCapacity();
    }

    //从队列尾部添加元素e，插入null元素会报空指针异常
    public void addLast(E e) {
        if (e == null)
            throw new NullPointerException();
        //第一次添加时tail=0，从数组第一次依次添加元素
        elements[tail] = e;
        //是不是想这里为什么要这样做，tail + 1不是就够了吗？
        //这里是考虑head值为0的情况，设elements.length = 16，当head为0，tail当前值为15时
        //实际上数组这时已经满了，但是怎么判断数组满了呢?
        //tail + 1 = 16, elements.length - 1 = 15， head = 0
        // 00010000 & 00001111 = 00000000 == head
        //这里是一处非常巧妙的做法，简单一行做了很多事 将tail+1的同时还能判断数组有没有满
        //与运算又能提高程序效率，真是一举多得!!!
        //需要注意的是，这里是把元素放在tail位置之后再把tail+1的，也就是说tail下标位置是没有值的，也就是含头不含尾
        if ( (tail = (tail + 1) & (elements.length - 1)) == head)
            //扩容1倍
            doubleCapacity();
    }

    //从队列头部添加元素e，插入null元素会报空指针异常，跟addFirst不同的是返回布尔值
    public boolean offerFirst(E e) {
        addFirst(e);
        return true;
    }

    //从队列尾部添加元素e，插入null元素会报空指针异常，跟addLast不同的是返回布尔值
    public boolean offerLast(E e) {
        addLast(e);
        return true;
    }

    //将队列首部的元素取出并移除
    public E removeFirst() {
        E x = pollFirst();
        //x==null，说明队列为空
        if (x == null)
            throw new NoSuchElementException();
        return x;
    }

    //将队列首部的元素取出并移除
    public E pollFirst() {
        int h = head;
        @SuppressWarnings("unchecked")
        //将队列头部的元素赋值给result
        E result = (E) elements[h];
        //result为null说明队列为空
        if (result == null)
            return null;
        //将头部元素置空
        elements[h] = null;
        //将头部指针向右移一位
        head = (h + 1) & (elements.length - 1);
        return result;
    }

    //将队列尾部元素取出并移除
    public E pollLast() {
        //当tail>0时，直接取tail - 1位置元素，tail位置为null
        //当tail=0时，取elements.length - 1处元素
        int t = (tail - 1) & (elements.length - 1);
        @SuppressWarnings("unchecked")
        E result = (E) elements[t];
        //result为null说明队列为空
        if (result == null)
            return null;
        //将头部元素置空
        elements[t] = null;
        //将取出到的元素位置索引赋给tail，tail处值为null，含头不含尾
        tail = t;
        return result;
    }

    //获取队列头部元素，不删除，没有则抛出异常
    public E getFirst() {
        @SuppressWarnings("unchecked")
        E result = (E) elements[head];
        if (result == null)
            throw new NoSuchElementException();
        return result;
    }

    //获取队列尾部元素，不删除，没有则抛出异常
    public E getLast() {
        @SuppressWarnings("unchecked")
        E result = (E) elements[(tail - 1) & (elements.length - 1)];
        if (result == null)
            throw new NoSuchElementException();
        return result;
    }

    //获取队列头部元素，不删除
    public E peekFirst() {
        // elements[head] is null if deque empty
        return (E) elements[head];
    }

    //获取队列尾部元素，不删除
    public E peekLast() {
        return (E) elements[(tail - 1) & (elements.length - 1)];
    }

    //移除队列中从头部开始第一次出现的元素o，equals比较
    public boolean removeFirstOccurrence(Object o) {
        //队列中不存在null元素
        if (o == null)
            return false;
        //取底层数组的最后一位
        int mask = elements.length - 1;
        //取队列首部的位置
        int i = head;
        //声明一个x变量，用来存储遍历的元素，避免在循环中多次声明
        Object x;
        //遍历队列，为空说明没有元素，结束遍历
        while ( (x = elements[i]) != null) {
            //找到第一个相同的元素，直接删除并返回true
            if (o.equals(x)) {
                delete(i);
                return true;
            }
            //没找到，继续遍历，当遍历到最后一个元素时，下个元素下标为0
            //如果elements.length=16,当 i = mask 时，i + 1 = 16, mask = 15
            // 00010000 & 00001111 = 00000000
            i = (i + 1) & mask;
        }
        return false;
    }

    //移除队列中从尾部开始第一次出现的元素o，equals比较
    public boolean removeLastOccurrence(Object o) {
        //队列中不存在null元素
        if (o == null)
            return false;
        //取底层数组的最后一位
        int mask = elements.length - 1;
        //从tail-1位置开始遍历，当tail=0时，从最后一位开始
        int i = (tail - 1) & mask;
        //声明一个x变量，用来存储遍历的元素，避免在循环中多次声明
        Object x;
        //遍历队列，为空说明没有元素，结束遍历
        while ( (x = elements[i]) != null) {
            //找到第一个相同的元素，直接删除并返回true
            if (o.equals(x)) {
                delete(i);
                return true;
            }
            //没找到，继续遍历，当遍历到下标为0时，下个元素为最后一个元素
            i = (i - 1) & mask;
        }
        return false;
    }

    //从队列尾部添加元素e，插入null元素会报空指针异常，跟addLast不同的是返回布尔值
    public boolean add(E e) {
        addLast(e);
        return true;
    }

    //从队列尾部添加元素e，插入null元素会报空指针异常，跟addLast不同的是返回布尔值
    public boolean offer(E e) {
        return offerLast(e);
    }

    //移除队列首部元素并返回
    public E remove() {
        return removeFirst();
    }

    //将队列首部的元素取出并移除
    public E poll() {
        return pollFirst();
    }

    //获取队列头部元素，不删除
    public E element() {
        return getFirst();
    }

    //获取队列尾部元素，不删除
    public E peek() {
        return peekFirst();
    }

    //从队列头部添加元素e，插入null元素会报空指针异常
    public void push(E e) {
        addFirst(e);
    }

    //移除队列首部元素并返回
    public E pop() {
        return removeFirst();
    }

    //检查队列中的元素是否正常
    private void checkInvariants() {
        assert elements[tail] == null;
        assert head == tail ? elements[head] == null :
            (elements[head] != null && elements[(tail - 1) & (elements.length - 1)] != null);
        assert elements[(head - 1) & (elements.length - 1)] == null;
    }

    //根据下标删除一个元素
    private boolean delete(int i) {
        //检查队列中的元素是否正常
        checkInvariants();
        //用一堆final变量来存储当前队列内部数据
        //数组
        final Object[] elements = this.elements;
        //数组最后一位
        final int mask = elements.length - 1;
        //队列头部
        final int h = head;
        //队列尾部
        final int t = tail;
        //设elements.length=16, h=11,t=9,i=13，mask主要是通过与运算将其中的负数转为正数
        //i-h=2
        //故这里的front其实就是指的要删除的位置前面有几个元素
        final int front = (i - h) & mask;
        //t-i=-4, 二进制0100 取反-> 1011 加1-> 1100 即12
        //故这里的back其实就是指的要删除的位置后面有几个元素
        final int back  = (t - i) & mask;

        // t-h=-2 二进制0010 取反-> 1101 加1-> 1110 即14
        //(t - h) & mask)主要是为了计算队列中元素个数
        //所以这里要删除的元素前面的元素肯定要小于总元素个数
        if (front >= ((t - h) & mask))
            throw new ConcurrentModificationException();

        // 要删除的元素位置右边的元素个数小于左边的情况
        if (front < back) {
            //如果要删除的元素在head-mask之间，把head位置和要删除的元素之间的元素右移一位即可
            if (h <= i) {
                System.arraycopy(elements, h, elements, h + 1, front);
            } else {
                //把要删除的元素到0位置的i个元素先右移一位
                System.arraycopy(elements, 0, elements, 1, i);
                //再把最后一位元素移到第一位
                elements[0] = elements[mask];
                //最后把head后面的元素右移一位
                System.arraycopy(elements, h, elements, h + 1, mask - h);
            }
            //把head位置元素置空null
            elements[h] = null;
            //重新计算head的位置
            head = (h + 1) & mask;
            return false;
        // 要删除的元素位置右边的元素个数大于左边的情况
        } else {
            //要删除的元素在0-tail之间,把i+1位置到tail之间的元素都右移一位
            if (i < t) {
                System.arraycopy(elements, i + 1, elements, i, back);
                tail = t - 1;
            } else {
                //要删除的元素在head-mask之间，把i+1到mask之间的元素都左移一位
                System.arraycopy(elements, i + 1, elements, i, mask - i);
                //再把第一位的元素放到最后一位
                elements[mask] = elements[0];
                //最后把1到tail之间的元素全部左移一位
                System.arraycopy(elements, 1, elements, 0, t);
                //重新计算tail的位置
                tail = (t - 1) & mask;
            }
            return true;
        }
    }

    //获取队列大小
    public int size() {
        return (tail - head) & (elements.length - 1);
    }

    //判断队列是否为空，默认head=0，tail=0，即head=tail，添加元素后head=tail时会自动扩容
    public boolean isEmpty() {
        return head == tail;
    }

    //返回一个迭代器
    public Iterator<E> iterator() {
        return new DeqIterator();
    }

    //判断队列中是否包含元素o，equals比较
    public boolean contains(Object o) {
        //队列中不存在null元素
        if (o == null)
            return false;
        //取数组最后一个位置
        int mask = elements.length - 1;
        //取队列头部
        int i = head;
        //声明一个x变量，用来存储遍历的元素，避免在循环中多次声明
        Object x;
        //从头部开始遍历，遇到null元素则停止遍历
        while ( (x = elements[i]) != null) {
            //含有元素o，返回true
            if (o.equals(x))
                return true;
            //否则取下一位元素
            i = (i + 1) & mask;
        }
        return false;
    }

    //移除队列中从头部开始第一次出现的元素o，equals比较
    public boolean remove(Object o) {
        return removeFirstOccurrence(o);
    }

    //清空队列
    public void clear() {
        int h = head;
        int t = tail;
        if (h != t) { // clear all cells
            //重置head与tail到初始状态
            head = tail = 0;
            int i = h;
            int mask = elements.length - 1;
            //从头部开始遍历，直到尾部停止
            do {
                //将元素依次置为空
                elements[i] = null;
                //获取下个元素位置
                i = (i + 1) & mask;
            } while (i != t);
        }
    }

    //将队列转为Object数组并返回
    public Object[] toArray() {
        return copyElements(new Object[size()]);
    }

    //将队列转为指定类型数组并返回
    public <T> T[] toArray(T[] a) {
        int size = size();
        if (a.length < size)
            a = (T[])java.lang.reflect.Array.newInstance(
                    a.getClass().getComponentType(), size);
        copyElements(a);
        if (a.length > size)
            a[size] = null;
        return a;
    }

    //克隆一份队列，浅克隆
    public ArrayDeque<E> clone() {
        try {
            @SuppressWarnings("unchecked")
            ArrayDeque<E> result = (ArrayDeque<E>) super.clone();
            result.elements = Arrays.copyOf(elements, elements.length);
            return result;
        } catch (CloneNotSupportedException e) {
            throw new AssertionError();
        }
    }

    //序列化队列
    private void writeObject(java.io.ObjectOutputStream s)
            throws java.io.IOException {
        s.defaultWriteObject();

        // Write out size
        s.writeInt(size());

        // Write out elements in order.
        int mask = elements.length - 1;
        for (int i = head; i != tail; i = (i + 1) & mask)
            s.writeObject(elements[i]);
    }

    //反序列化队列
    private void readObject(java.io.ObjectInputStream s)
            throws java.io.IOException, ClassNotFoundException {
        s.defaultReadObject();

        // Read in size and allocate array
        int size = s.readInt();
        int capacity = calculateSize(size);
        SharedSecrets.getJavaOISAccess().checkArray(s, Object[].class, capacity);
        allocateElements(size);
        head = 0;
        tail = size;

        // Read in all elements in the proper order.
        for (int i = 0; i < size; i++)
            elements[i] = s.readObject();
    }